向量旋转的三种表示方法：旋转矩阵 / 欧拉角 / 四元数

斐夷所非

已于 2025-02-08 09:12:49 修改

阅读量3.9k

点赞数 35

分类专栏： mechatronics 文章标签：向量旋转

于 2024-11-10 00:18:54 首次发布

本文链接：https://blog.csdn.net/u013669912/article/details/143083662

版权

mechatronics 专栏收录该内容

4 篇文章

订阅专栏

注：本文为 “旋转矩阵 / 欧拉角 / 四元数” 相关文章的合辑。

如有内容异常，请查看原文。

彻底搞懂 “旋转矩阵 / 欧拉角 / 四元数” 三维旋转

肥肥胖胖是太阳已于 2022-02-14 14:14:22 修改

向量的旋转一共有三种表示方法：旋转矩阵、欧拉角和四元数。

接下来介绍一下每种旋转方法的原理以及相互转换方式。

旋转矩阵

坐标变换的作用

在一个机器人系统中，每个测量元件测量同一物体得出的信息是不一样的，原因就在于 “每个测量元件所测量的数据是基于不同坐标系所测量的”，例如：

在这辆车中有激光雷达 M 和激光雷达 W，这两个雷达测量的数据截然不同，但是这辆汽车相对于测量物体的位置是唯一的，这就说明 “由不同位置雷达测量的数据代表的物理含义（即都表示汽车与被测物体的相对位置）是相同的”。那既然被测物体在不同坐标系中的坐标不同但物理含义相同，这就涉及到不同坐标系中坐标的相互转化。下面这个视频将使你对坐标变换有一个初步的认识：

无所不能的矩阵 - 三维图形变换 _bilibili
https://www.bilibili.com/video/BV1b34y1y7nF/

常用出发与坐标系原点终止于坐标系中坐标点的向量来表示坐标系中坐标点相对于坐标原点的位置（距离 + 方位）。坐标系的相互转化必须以地球坐标系为媒介才可以实现，即坐标系的相互转化必须已知 “任意坐标系中各个坐标轴在 world 坐标系中的坐标”：

会疑惑：world 坐标系是什么？

在空间中会有 n+1 个坐标系，其中只有一个坐标系起到标定作用，也就是说 “其他 n 个坐标系全都是基于该坐标系找到自己在空间中的位置的”。只有大家都知道了自己在空间中的具体位置，坐标转换才可以顺利进行下去。

位姿变换

基于 O1 的世界坐标系与基于 O2 的坐标系如下所示：

在描述机器人运动时，常常提及 “位姿”，其实位姿是一个合成词，可以将其拆解为 “位置 + 姿态”。位置就是指 “机器人某个运动关节 / 测量传感器在世界坐标系中的具体位置，姿态就是”基于该点的坐标系相较于世界坐标系所进行的旋转 “，如下所示：

坐标变换中旋转的实质

坐标变换的实质就是 “投影”。首先，解读一下向量是如何转化为坐标的：

理解向量坐标的由来对于理解坐标变换的实质至关重要！接下来考虑一下单位向量在坐标系中的投影：

单位向量在坐标系中的投影正好为向量 P 与各个坐标轴夹角的余弦值。

将坐标系 A 作为参考坐标系（world 坐标系），基于坐标系 A 表示坐标系 B 的各个坐标轴并且将各个向量单位化，由此得到一个旋转矩阵，旋转矩阵各个元素的含义如下：

先前提到过，向量坐标的计算无非就是投影，那么向量坐标从坐标系 B 转换至坐标系 A 无非就是两次投影而已：

坐标转换的实际意义无非就是将向量 P 在坐标系 A 中各个轴的投影分别累加起来形成一个新的坐标。那问题来了，累加如何操作呢？这就涉及旋转矩阵以及矩阵乘法运算了。

其实，这个矩阵的乘法与卷积有着异曲同工之妙。旋转矩阵的性质：

坐标变换中平移的实质

向量可以在坐标系中任意移动，只要不改变向量的方向和大小，向量的属性不会发生变化。但是研究的是坐标系 B 中一个坐标点在坐标系 A 中的映射，因此需要考虑坐标系 B 的原点 O2 相较于坐标系 A 原点 O1 平移的距离。

每个基于坐标系 B 的向量先进性旋转变换，再与向量 O1O2 求和即可得到向量 P 再坐标系 A 中的实际映射。

如何计算坐标系 B 各坐标轴在坐标系 A 上的投影？（多坐标变换）

首先，要知道世界坐标系下坐标系 A / 坐标系 B 的各个坐标轴在世界坐标系（参考坐标系）的坐标：

使用旋转矩阵的性质可以得到坐标系 B 变换至坐标系 A 的旋转矩阵：

坐标变换流程如下：

如何实现坐标变换？

将 P 点在坐标系 B 中的坐标转化为 P 点在坐标系 A 中对应的坐标：

坐标变换 = 旋转 + 平移，因此坐标变换表达式如下所示：

这样不利于矩阵运算，可以改写为如下形式：

其中 $O_1O_2$ 是从 $O_1$ 指向 $O_2$ 的向量。

欧拉角

欧拉角的作用

欧拉角遵循的是右手系规则，即大拇指指向坐标轴正方向，四指旋转的方向即为转动的正方向，欧拉角包含三个自由量：yaw(偏航角)、pitch(俯仰角)、roll(翻滚角)。

将三次旋转分开讨论，以绕 Z 轴旋转为例来进行说明：

绕 Z 轴旋转的三维立体图如上所示，为了方便，查看一下二维旋转图：

欧拉角与旋转矩阵

欧拉角可以转化为旋转矩阵，并且利用旋转矩阵的知识进行旋转操作。向量在二维平面上旋转可以让联想到向量在复平面中的旋转：

设向量 P 的坐标为( $x, y$ )，则 $XO Y$ 平面变换公式如下所示：

由于 “绕谁谁不变” 的原则，因此 Z 轴坐标不会发生改变，最终 Z 轴旋转变换公式如下所示：

同理，可以按照同样的方式得出到 X/Y 轴旋转的公式：

旋转矩阵的旋转顺序分为外旋（x->y->z）和内旋（z->y->x），一般使用外旋的顺序：

欧拉角的弊端

欧拉角有三个分别为 yaw(偏航角)、pitch(俯仰角)、roll(翻滚角)，代表着绕着 Z/Y/X 轴旋转的角度，相当于有三个独立变量（自由度）控制一架飞机进行如下旋转操作：

但是当任何一个坐标轴旋转角度为 90 度时，就会有两个轴的旋转动作起到对总体旋转结果相同的效果，这就被称为 “死锁 “，动态图如下所示：

上面的动画展示了绕 X 轴旋转 90 度之后，Y 轴与 Z 轴正方向同向，这就导致绕 Y 轴旋转 θ 度与绕 Z 轴的正方向旋转 θ 度有同样的效果，即丢失了一个自由度。“丢失了一个自由度 “也就意味着真正起到旋转作用的只有 Y 轴和 X 轴（或者 Z 轴和 X 轴），即飞机无法绕着原 Z 轴正方向进行旋转操作。

” 死锁 “现象在二维平面图中如下所示：

无论绕 X 轴正方向 / 反方向旋转 90 度，都会导致 Y/Z 轴正方向罗在一条直线上！为了解决 “死锁 “的问题，要使用四个自由量，这就引出了” 四元数 “的概念。

四元数

数学的美妙不在于形象的表达变换的逻辑，而在于抽象简单的给出表达式。四元数就是如此，四元数的三维表达晦涩难懂，但是四元数的表达式可以优雅的表达三维中的旋转操作，不但避免了欧拉角的死锁问题而且也避免了旋转矩阵的复杂计算。

四元数的可视化 _哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1SW411y7W1/

上述四元数的物理解释较难理解，而我喜欢把它理解为一种旋转算法。数学之美就在于其揭示了许多新的计算方法，幸运的是，四元数就是一种用于物体旋转的计算方法。

三维旋转

该部分为后续探究三维旋转与四元数的关系打下基础。

向量 V 围绕着向量 U 进行三维空间中的旋转操作得到向量 V‘，其中向量 U 为单位向量。现在，为了简化向量的旋转操作，分解向量 V：

向量 V 在向量 U 平行方向上的分量不参与旋转，参与旋转的是向量 V 垂直于向量 U 的分量：

同样，旋转后的向量 V’ 也由垂直于向量 U 和平行于向量 U 两部分分量矢量叠加而成：

最难求出的是向量 V‘垂直于向量 U 的部分，以二维平面图为例进行求解：

找出向量 Vw（与原垂直分量垂直）就可以对向量进行分解，要求 Vw 需了解三维图中 Vw：

可以清楚的观察到，Vw 与单位向量 U 以及向量 V 原垂直分量垂直，故可以得出：

结合向量投影的知识可以得到旋转后向量 V 的表达式：

三维复数

四元数包含了四个实参数以及三个虚部（一个实部三个虚部），从四维角度来看如下图所示：

Re 实部与 i/j/k 三个虚部都垂直，并且在坐标系 U 内部三个虚部两两垂直形成了一个三维坐标系，并且三维复数的运算规则如下所示（aij=ai*aj）：

Re 实部与 i/j/k 三个虚部都垂直，并且在坐标系 U 内部，三个虚部两两垂直形成了一个三维坐标系。并且，三维复数的运算规则如下所示（ $a_{ij} = a_i \cdot a_j$ ）：

	1	i	j	k
1	1	i	j	k
i	i	-1	k	-j
j	j	-k	-1	i
k	k	j	-i	-1

上面这个看似简单的表格就决定了四元数的一切性质，你或许看起来很困惑：这个运算法则如何得到，又有何物理意义？

回答是：这个乘法是由数学家规定的，其物理意义代表了 “按照特定的方向旋转 90 度的操作”，如果你问我为何这个乘法被定义为三维空间中坐标系旋转 90 度的操作，那如下 YouTube 上的评论会一定程度上取消你的疑虑：

答案就是：可以借助这种乘法法则找到三维旋转中的某种规律性的东西。

四元数的定义

与复数类似，因为四元数其实就是对于基 {1, 𝑖, 𝑗, 𝑘} 的线性组合，四元数也可以写成向量的形式：

$\text{q}=\left[ \begin{array}{c} a \\ b \\ c \\ d \\ \end{array} \right]$

除此之外，经常将四元数的实部与虚部分开，并用一个三维的向量来表示虚部，将它表示为标量和向量的有序对形式：

这里可能还感觉到迷茫，没关系，一步一步来！

四元数的性质

研究四元数的性质是为了纯四元数和三维空间中的旋转操作做铺垫。

四元数乘法

其实，也可以将其写成矩阵形式，为后面四元数转旋转矩阵做铺垫：

注意：左乘与右乘不同，这一点与矩阵的性质类似，但是四元数乘法与矩阵乘法完全是两个概念，以魔方旋转为例：

因为物体的 6 个侧面一般并不相同（相当于有 6 个独立不相同的面），按照 “左转 -> 下转” 和 “下转 -> 左转” 的顺序得到的 Y 轴正方向的平面并不一样，所以三维旋转不可逆。

现在从物理含义的角度理解一下左乘和右乘的具体含义：

左乘旋转四元数（左为操作动作，右为被操作对象）

右乘旋转四元数（右为操作动作，左为被操作对象）

四元数旋转公式的含义

这里，结合左乘与右乘的相关知识就可以清楚的了解乘法法则中的变换关系：

乘法法则	1	i	j	k
1	1	i	j	k
i	i	-1	k	-j
j	j	-k	-1	i
k	k	j	-i	-1

以 $j * i = - k ， i * i = - 1 ， k * i = j$ 来进行说明（右乘 i）：

纯四元数

在正式进入四元数的讨论之前，还需要更多关于四元数的定义。如果一个四元数能写成这样的形式：

$u=\left[ 0,\ \overset{\to }{\mathop{u}}\, \right]$

那则称𝑣为一个纯四元数，即仅有虚部的四元数。因为纯四元数仅由虚部的 3D 向量决定，可以将任意的 3D 向量转换为纯四元数。纯四元数有一个很重要的特性：如果有两个纯四元数 𝑣 = [0, v], 𝑢 = [0, u]，那么由四元数乘法可以得到：

四元数的共轭

发现四元数的性质与矩阵相似。当四元数模值为 1，则该四元数被称为单位四元数。

四元数与三维旋转

向量转四元数

三维空间中向量的旋转全部可以写成纯四元数的形式：

一定要对这些符号留有印象，对后面的四元数转化为旋转矩阵的理解很有帮助。

三维旋转转四元数

向量 V 绕向量 U 进行三维空间中的旋转最重要的是向量 V 沿向量 U 垂直方向上的分量的旋转：

注意：

那么接下来可以将三维旋转与纯四元数进行转化：

其中，四元数 q 有以下性质：

其中，最容易误解的还是复数虚部的平方，其与向量 U 的模值无关：

由此可得，该四元数为单位四元数，但是不是纯四元数。这里还需要两个定理：

① 定理一：

从物理意义出发也可以理解：向量 V 平行于向量 U 的分量绕向量 U 旋转相当于没旋转。

② 定理二：

证明如下所示：

现在最精彩的来了，看上面的式子复杂且不美观，那现在使用一些技巧来旋转式子变得美观些：

最终得到四元数与三维旋转的对应关系：

旋转矩阵与四元数

前面介绍过左乘和右乘在矩阵转化时的区别，因此可以按照乘法法则将四元数转化为如下所示的三维旋转矩阵：

上述结论可以结合前面提到过的 “左乘 / 右乘” 的知识对上述公式进行巧记：

四元数与欧拉角的转化

一个展示欧拉角与四元数动态变换关系的网站：

Quaternions - Visualisation

https://quaternions.online/

其中，重点注意 atan2(…) 与 atan(…) 函数的区别：

atan() 函数的值域为 $[- π /2, π /2]$ ，但是 atan2() 函数的值域为 $[- π, π]$ 。atan2() 函数弥补了 atan() 函数识别不出第一象限和第三象限、第四象限和第二象限的缺陷。atan2() 函数是求解方位角的最佳选择。

#define PI (std::acos(-1))  
  
int main(int argy, char* argv[])  
{  
    std::cout << "---------第一象限---------" << std::endl;  
    double y1 = 1, x1 = 1;  
    std::cout << "std::atan(y1/x1)=" << std::atan(y1 / x1) / PI * 180 << std::endl;  
    std::cout << "std::atan2(y1,x1)=" << std::atan2(y1, x1) / PI * 180 << std::endl;  
  
    std::cout << "---------第二象限---------" << std::endl;  
    double y4 = 1, x4 = -1;  
    std::cout << "std::atan(y4/x4)=" << std::atan(y4 / x4) / PI * 180 << std::endl;  
    std::cout << "std::atan2(y4,x4)=" << std::atan2(y4, x4) / PI * 180 << std::endl;  
  
    std::cout << "---------第三象限---------" << std::endl;  
    double y3 = -1, x3 = -1;  
    std::cout << "std::atan(y3/x3)=" << std::atan(y3 / x3) / PI * 180 << std::endl;  
    std::cout << "std::atan2(y3,x3)=" << std::atan2(y3, x3) / PI * 180 << std::endl;  
  
    std::cout << "---------第四象限---------" << std::endl;  
    double y2 = -1, x2 = 1;  
    std::cout << "std::atan(y2/x2)=" << std::atan(y2 / x2) / PI * 180 << std::endl;  
    std::cout << "std::atan2(y2,x2)=" << std::atan2(y2, x2) / PI * 180 << std::endl;  
  
    return 0;  
}

运行结果如下所示：

四元数、欧拉角、旋转矩阵、旋转向量之间的转换

泠山已于 2024-04-11 16:33:55 修改

1. 欧拉旋转定理

在运动学里，欧拉旋转定理(Euler's rotation theorem)表明，在三维空间里，假设一个刚体在做一个旋转的时候，刚体内部至少有一点固定不动，则此位移等价于一个绕着包含那固定点的固定轴的旋转。

2. 轴角表示

旋转一个向量从 $a$ 到 $b$ ，轴角为 $(u,\theta)$ ，如下图所示：

罗德里格斯公式：

$b=acos\theta+(u\times a)sin\theta+u(u\cdot a)(1-cos\theta)$

2.1 旋转性质

$(u,\theta)$ 和 $(-u,-\theta)$ 为相同旋转。
$(u,-\theta)$ 为 $(u,\theta)$ 的逆旋转。
旋转运算是不能交换的，如：
$a=\left[\begin{array}{lll}3 & 0 & 0\end{array}\right]^{\top} \quad\left(u_{1}, \theta_{1}\right)=\left(\left[\begin{array}{lll}1 & 0 & 0\end{array}\right]^{\top}, 90^{\circ}\right) \quad\left(u_{2}, \theta_{2}\right)=\left(\left[\begin{array}{lll}0 & 1 & 0\end{array}\right]^{\top}, 90^{\circ}\right)$

情况一：

旋转 $a$ $(u_1,\theta_1)$ ，得到 $b=a=\left[\begin{array}{lll}3 & 0 & 0\end{array}\right]^{\top}$
旋转 $b$ $(u_2,\theta_2)$ ，得到 $c=\left[\begin{array}{lll}0 & 0 & 3\end{array}\right]^{\top}$

情况二：

旋转 $a$ $(u_2,\theta_2)$ ，得到 $b=a=\left[\begin{array}{lll}0 & 0 & 3\end{array}\right]^{\top}$
旋转 $b$ $(u_1,\theta_1)$ ，得到 $c=\left[\begin{array}{lll}0 & 3 & 0\end{array}\right]^{\top}$

3. 罗德里格斯公式

向量 $a, b$ 可以被分解成相对于 $u$ 的正交 $(a_{\perp}, b_{\perp})$ 和平行 $a_{\|}, b_{\|})$ 分量。

此时以下关系是成立的：

$a_{\|} = b_{\|}$

$b_{\perp} = a_{\perp} \cos \theta + k \sin \theta$

因此：

$\begin{aligned} b &= b_{\perp} + b_{\|} \\ &= b_{\perp} \cos \theta + k \sin \theta + u(u \cdot a) \\ &= a \cos \theta - u(u \cdot a) \cos \theta + (u \times a) \sin \theta + u(u \cdot a) \\ &= a \cos \theta + (u \times a) \sin \theta + u(u \cdot a)(1 - \cos \theta) \end{aligned}$

4. pitch yaw roll方向

roll: 翻滚角，顺时针翻滚即正值，逆时针翻滚为负值

yaw(heading): 航向角

pitch: 俯视角，俯仰是从局部 $x y$ 平面的旋转

5. 内旋和外旋

按旋转的坐标系分为内旋(intrinsic rotation)和外旋(extrinsic rotation)。

内旋: 绕物体自身的坐标系( $o bj ec t - s p a ce$ )旋转，举个例子，一个 $(\phi, \theta, \psi)$ $(x yz, in t r in s i c)$ 的欧拉角，指绕物体的 $X$ 轴转 $\phi$ 后，再绕物体的 $y^{'}$ 轴(这里用 $y^{'}$ 表示这个新的 $Y$ 轴已经和一开始世界坐标系下的那个物体的 $Y$ 轴不一样了)旋转 $\theta$ ，最后绕 $z^{'}$ 轴旋转 $\psi$ ，每一次旋转都会改变下一次旋转的轴。这种情况下旋转的轴是动态( $m o v in g a x i s$ )的。

外旋: 绕惯性系( $u p r i g h t - s p a ce$ )旋转( $u p r i g h t s p a ce$ 指基向量平行于（ $w or l d - s p a ce$ ）或（ $p a re n t - s p a ce$ ），原点与（ $o bj ec t - s p a ce$ ）的原点重合的空间)。也就是说，无论是三步旋转中的哪一步，轴都是固定不会动的。

内旋与外旋的转换关系：互换第一次和第三次旋转的位置则两者结果相同。例如 $Z - Y - X$ 旋转的内部旋转和 $X - Y - Z$ 旋转的外部旋转的旋转矩阵相同。

证明：

假设绕 $X Y Z$ 三个轴旋转的角度分别为 $\alpha$ $\beta$ $\gamma$ ，则三次旋转的旋转矩阵计算方法如下：

$R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{bmatrix}$

$R_y(\beta) = \begin{bmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{bmatrix}$

$R_z(\gamma) = \begin{bmatrix} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{bmatrix}$

按照内旋方式， $Z - Y - X$ 旋转顺序（指先绕自身轴 $Z$ ，再绕自身轴 $Y$ ，最后绕自身轴 $X$ ），可得旋转矩阵(内旋是右乘)：

$R_1=R_{z}(\gamma) * R_{y}(\beta) * R_{x}(\alpha)$

按照外旋方式， $X - Y - Z$ 旋转顺序（指先绕固定轴 $X$ ，再绕固定轴 $Y$ ，最后绕固定轴 $Z$ ），可得旋转矩阵(外旋是左乘)：

$R_2=R_{z}(\gamma) * R_{y}(\beta) * R_{x}(\alpha)$

因此 $R 1 = R 2$ ， $Z Y X$ 顺序的内旋等价于 $X Y Z$ 顺序的外旋。

SLAM 十四讲中提到的常用旋转顺序是 $Z - Y - X$ ，对应 $RP Y (R o ll - P i t c h - Ya w)$ 角，指的就是内旋（绕自身轴） $Z - Y - X$ 顺序。而欧拉角转换成旋转矩阵（相对于世界坐标系的旋转矩阵）通常是按外旋方式（绕固定轴），即 $X - Y - Z$ 顺序，所以旋转矩阵为：

$R_2=R_{z}(\gamma) * R_{y}(\beta) * R_{x}(\alpha)$

6. 使用哪种表示方法？

奇异性和不连续性: 用很少的参数表示可能导致数值问题：
欧拉角(3)：
– 奇异性：万向锁配置
– 不连续性：从 0° 跳变到 360°

旋转向量(3)：
– 不连续性：从 0° 跳变到 360°

旋转矩阵(9) / 四元数(4)：
– 没有奇异性或不连续性
几何解释: 有些表示法更容易用几何解释。它们更接近原始的传感器测量，也更容易与人类用户交互(显示或输入)
欧拉角：
– 参数是接近几何解释的角度和轴

旋转矩阵 / 四元数：
– 参数是正弦/余弦函数，其几何解释有些无关紧要

7. 四元数、欧拉角、旋转矩阵、旋转向量之间的转换

7.1 旋转向量

初始化旋转向量：旋转角为 $a lp ha$ ，旋转轴为 $(x, y, z)$

Eigen::AngleAxisd rotation_vector(alpha,Vector3d(x,y,z))；

旋转向量转旋转矩阵

Eigen::Matrix3d rotation_matrix;
rotation_matrix=rotation_vector.matrix();

Eigen::Matrix3d rotation_matrix;
rotation_matrix=rotation_vector.toRotationMatrix();

旋转向量转欧拉角( $Z - Y - X$ 内旋，即 $RP Y$ )

//(2,1,0)表示旋转顺序ZYX，数字越小表示优先级越高
Eigen::Vector3d eulerAngle=rotation_vector.matrix().eulerAngles(2,1,0);

旋转向量转四元数

Eigen::Quaterniond quaternion(rotation_vector);

7.2 旋转矩阵

初始化旋转矩阵

Eigen::Matrix3d rotation_matrix;
rotation_matrix<<x_00,x_01,x_02,x_10,x_11,x_12,x_20,x_21,x_22;

旋转矩阵转旋转向量

Eigen::AngleAxisd rotation_vector(rotation_matrix);

Eigen::AngleAxisd rotation_vector;
rotation_vector=rotation_matrix;

Eigen::AngleAxisd rotation_vector;
rotation_vector.fromRotationMatrix(rotation_matrix);

旋转矩阵转欧拉角( $Z - Y - X$ 内旋，即 $RP Y$ )

Eigen::Vector3d eulerAngle=rotation_matrix.eulerAngles(2,1,0);

旋转向量转四元数

Eigen::Quaterniond quaternion(rotation_matrix);
Eigen::Quaterniond quaternion;
quaternion=rotation_matrix;

7.3 欧拉角

初始化欧拉角( $Z - Y - X$ ，即 $RP Y$ )

Eigen::Vector3d eulerAngle(yaw,pitch,roll);

欧拉角转旋转向量

Eigen::AngleAxisd rollAngle(AngleAxisd(eulerAngle(2),Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(AngleAxisd(eulerAngle(1),Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(AngleAxisd(eulerAngle(0),Vector3d::UnitZ()));
Eigen::AngleAxisd rotation_vector;
rotation_vector=yawAngle*pitchAngle*rollAngle;

欧拉角转旋转矩阵

Eigen::AngleAxisd rollAngle(AngleAxisd(eulerAngle(2),Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(AngleAxisd(eulerAngle(1),Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(AngleAxisd(eulerAngle(0),Vector3d::UnitZ()));
Eigen::Matrix3d rotation_matrix;
rotation_matrix=yawAngle*pitchAngle*rollAngle;

欧拉角转四元数

Eigen::AngleAxisd rollAngle(AngleAxisd(eulerAngle(2),Vector3d::UnitX()));
Eigen::AngleAxisd pitchAngle(AngleAxisd(eulerAngle(1),Vector3d::UnitY()));
Eigen::AngleAxisd yawAngle(AngleAxisd(eulerAngle(0),Vector3d::UnitZ()));
Eigen::Quaterniond quaternion;
quaternion=yawAngle*pitchAngle*rollAngle;

7.4 四元数

初始化四元数

Eigen::Quaterniond quaternion(w,x,y,z);

四元数转旋转向量

Eigen::AngleAxisd rotation_vector(quaternion);

Eigen::AngleAxisd rotation_vector;
rotation_vector=quaternion;

四元数转旋转矩阵

Eigen::Matrix3d rotation_matrix;
rotation_matrix=quaternion.matrix();

Eigen::Matrix3d rotation_matrix;
rotation_matrix=quaternion.toRotationMatrix();

四元数转欧拉角( $Z - Y - X$ ，即 $RP Y$ )

// yaw pitch roll
Eigen::Vector3d eulerAngle=quaternion.matrix().eulerAngles(2,1,0);

下面代码与上面接口可得到相同结果：

static Eigen::Vector3d getEulerFromQuternion(const Eigen::Quaterniond& q){
    double roll, pitch ,yaw;

    // roll (x-axis rotation)
    double sinr_cosp = +2.0 * (q.w() * q.x() + q.y() * q.z());
    double cosr_cosp = +1.0 - 2.0 * (q.x() * q.x() + q.y() * q.y());
    roll = atan2(sinr_cosp, cosr_cosp);

    // pitch (y-axis rotation)
    double sinp = +2.0 * (q.w() * q.y() - q.z() * q.x());
    if (fabs(sinp) >= 1)
        pitch = copysign(M_PI / 2, sinp); // use 90 degrees if out of range
    else
        pitch = asin(sinp);

    // yaw (z-axis rotation)
    double siny_cosp = +2.0 * (q.w() * q.z() + q.x() * q.y());
    double cosy_cosp = +1.0 - 2.0 * (q.y() * q.y() + q.z() * q.z());
    yaw = atan2(siny_cosp, cosy_cosp);

    Eigen::Vector3d eulers;
    eulers << yaw, pitch, roll;
    return eulers;
}

python 实现四元数、欧拉角、旋转矩阵、旋转向量的相互转换

大大大管的笔记本已于 2023-07-19 11:47:14 修改

在实际项目中，经常会遇到各种转换，比如我遇到的就是四元数转旋转矩阵、欧拉角转旋转矩阵、旋转向量转旋转矩阵等等。

时不时还需要看一下自己的算法计算的角度是否正确，所以需要转换到欧拉角。

每次都会忘记对应的API是啥，在哪，之类的问题。这次索性就整理到一起去算了。

1. 旋转向量转旋转矩阵

import cv2
import numpy as np
def rotvector2rot(rotvector):
    Rm = cv2.Rodrigues(rotvector)[0]
    return Rm
rotvector = np.array([[0.223680285784755,	0.240347886848190,	0.176566110650535]])
print(rotvector2rot(rotvector))
# 输出
# [[ 0.95604131 -0.14593404  0.2543389 ]
#  [ 0.19907538  0.95986385 -0.19756111]
#  [-0.21529982  0.23950919  0.94672136]]

2. 四元数转欧拉角

from scipy.spatial.transform import Rotation as R
def quaternion2euler(quaternion):
    r = R.from_quat(quaternion)
    euler = r.as_euler('xyz', degrees=True)
    return euler
quaternion = [0.03551,0.21960,-0.96928, 0.10494]
print(quaternion2euler(quaternion))
# 输出
# [ -24.90053735    6.599459   -169.1003646 ]

3. 欧拉角转四元数

from scipy.spatial.transform import Rotation as R
def euler2quaternion(euler):
    r = R.from_euler('xyz', euler, degrees=True)
    quaternion = r.as_quat()
    return quaternion
euler = [-24.90053735, 6.599459, -169.1003646]
print(euler2quaternion(euler))
# 输出
# [ 0.03550998  0.21959986 -0.9692794   0.10493993]

4. 欧拉角转旋转矩阵

from scipy.spatial.transform import Rotation as R
def euler2rot(euler):
    r = R.from_euler('xyz', euler, degrees=True)
    rotation_matrix = r.as_matrix()
    return rotation_matrix
euler = [-24.90053735,    6.599459,   -169.1003646]
print(euler2rot(euler))
# 输出
# [[-0.9754533   0.21902821 -0.02274859]
#  [-0.18783626 -0.88152702 -0.43316008]
#  [-0.11492777 -0.41825442  0.90102988]]

5. 旋转矩阵转欧拉角

import numpy as np
import math
def isRotationMatrix(R):
    Rt = np.transpose(R)
    shouldBeIdentity = np.dot(Rt, R)
    I = np.identity(3, dtype=R.dtype)
    n = np.linalg.norm(I - shouldBeIdentity)
    return n < 1e-6
def rot2euler(R):
    assert (isRotationMatrix(R))
    sy = math.sqrt(R[0, 0] * R[0, 0] + R[1, 0] * R[1, 0])
    singular = sy < 1e-6
    if not singular:
        x = math.atan2(R[2, 1], R[2, 2]) * 180 / np.pi
        y = math.atan2(-R[2, 0], sy) * 180 / np.pi
        z = math.atan2(R[1, 0], R[0, 0]) * 180 / np.pi
    else:
        x = math.atan2(-R[1, 2], R[1, 1]) * 180 / np.pi
        y = math.atan2(-R[2, 0], sy) * 180 / np.pi
        z = 0
    return np.array([x, y, z])
rot = np.array([[-1.01749712e-02,  9.99670705e-01, -2.35574076e-02],
 [-9.99890780e-01, -1.04241019e-02, -1.04769347e-02],
 [-1.07190495e-02,  2.34482322e-02,  9.99667586e-01]])
print(rot2euler(rot))
# 输出
# [  1.34368509   0.61416806 -90.58302646]'
运行
运行

6. 四元数转旋转矩阵

from scipy.spatial.transform import Rotation as R
def quaternion2rot(quaternion):
    r = R.from_quat(quaternion)
    rot = r.as_matrix()
    return rot
quaternion = [0.03551, 0.21960, -0.96928, 0.10494]
print(quaternion2rot(quaternion))
# 输出
# [[-0.9754533   0.21902821 -0.02274859]
#  [-0.18783626 -0.88152702 -0.43316008]
#  [-0.11492777 -0.41825442  0.90102988]]

图像引擎里的旋转变换–Euler Angle & Quaternion

刘子豪375 _zhihu 发布于 2020-03-30 23:21

在实时图形渲染里，矩阵变换是计算物体位置、物体形状、光照以及摄像机方向等等重要操作的基本载体。而在矩阵变换中有一种特殊的变换形式–旋转变换。本文将主要介绍旋转变换的基础原理，不会讲解具体API的应用。

旋转变换有三种主要的表达形式–rotation matrix（旋转矩阵），euler transform(欧拉变换)，和quaternion transform（四元数变换）。本文将对rotation matrix（旋转矩阵），欧拉变换和四元数变换的基本原理、转换关系和适用情况进行介绍。

1.概念介绍及推导原理

Rotation Matrix

在 transform 中旋转最直接的表现形式，具体原理也很简单：

对于二位坐标中的一个

$vector\,\,V (v_{x}, v_{y})$ ,

参数化 V，我们得到

$=（rcos\theta, rsin\theta）$

如果我们把这个向量逆时针旋转 $\phi$ ，此时向量变成

$(rcos（\theta+\phi）, rsin(\theta+\phi))$ ，

通过三角变换，有

$(r(cos\theta cos\phi - sin\theta sin\phi),r(sin\theta cos\phi +cos\theta sin\phi))$

如果变成矩阵的形式，我们得到

$\begin{aligned} V &= \begin{bmatrix} r\cos(\theta + \phi) \\ r\sin(\theta + \phi) \end{bmatrix} \\ &= \begin{bmatrix} r(\cos\theta \cos\phi - \sin\theta \sin\phi) \\ r(\sin\theta \cos\phi + \cos\theta \sin\phi) \end{bmatrix} \\ &= \begin{bmatrix} \cos\theta & -\sin\phi \\ \sin\theta & \cos\phi \end{bmatrix} \begin{bmatrix} r\cos\theta \\ r\sin\theta \end{bmatrix} \end{aligned}$

和原 vector 比较，我们有 rotation $R(\theta)=\begin{bmatrix} cos\theta & -sin\phi\\ sin\theta & cos\phi \end{bmatrix}$

如果我们回到三维坐标系，如果一个向量 V（ $x, y, z$ ）是关于x轴旋转的，那么对于 V 来说， $x$ 坐标是不会产生变换的，变换的维度在 $yz$ 平面上。因此，在 $\,\, transform$ （齐次变换）的 $\, matrix$ 应该是

$R_{x}(\phi)= \begin{bmatrix} 1&0&0&0\\ 0&cos\theta & -sin\phi&0\\ 0&sin\theta & cos\phi&0\\ 0&0&0&1 \end{bmatrix}$

同理

$R_{y}(\phi)= \begin{bmatrix} cos\theta &0& sin\phi&0\\ 0&1&0&0\\ -sin\theta &0& cos\phi&0\\ 0&0&0&1 \end{bmatrix}$

$R_{z}(\phi)= \begin{bmatrix} cos\theta & -sin\phi&0&0\\ sin\theta & cos\phi&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{bmatrix}$

矩阵的 trace，对角线元素之和等于 $1+2cos\theta$

Euler Transform

首先介绍 head， pitch, roll 的概念。本文将沿用 real time rendering 一书中的写法，有的地方也写做 $ro ll ， p i t c h, y a w$ , 图示如下：

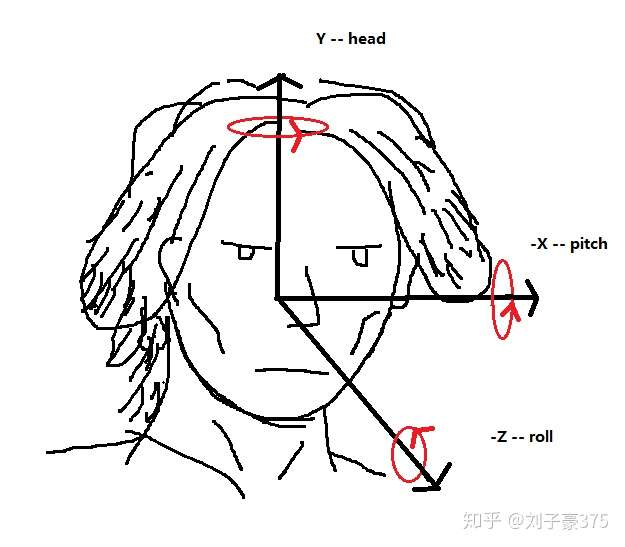
懒得用别人的图写来源就随手图自己画了张:^)

一般情况下，camera都会放在-z上，在world space的坐标为(0,0,-1)。

回到欧拉角当中，欧拉矩阵将关于三坐标轴的旋转结合在一起，因此有了：

$E(head, pitch, roll) = R_{z}(roll)R_{x}(pitch)R_{y}(head)$

综合上面关于关于各个坐标轴矩阵的计算，有：

$\begin{bmatrix} cosr & -sinr&0\\ sinr & cosr&0\\ 0&0&1\\ \end{bmatrix} \ \begin{bmatrix} 1&0&0\\ 0& cosp & -sinp\\ 0&sinp & cosp\\ \end{bmatrix} \ \begin{bmatrix} cosh &0& sinh\\ 0&1&0\\ -sinh &0& cosh\\ \end{bmatrix}$

此时注意 $h, p, r$ 相乘的顺序为逆序。

由欧拉角转换为 Matrix 3x3 的函数也十分简单明了，照搬上述公式即可，不再赘述。

对于设计师来说，欧拉角的优势是直接，在小角度变换时方便，然而欧拉角有一些严重的局限性：

gimbal lock：万向节锁

动图来自 wikipedia

动图清晰地展示了什么是万向锁（gimbal lock）——即失去一个维度上的自由度。具体来说，当绿色环与粉色环对齐时，蓝色环和粉色环产生的旋转效果相同。这导致了一个问题：由于仅锁定了一个旋转维度，原本应由三维旋转变为二维旋转，但最终却只剩下了一维旋转。这便是所谓的“失去一个维度上的自由度”。

从数学的角度来讲，在上面提到的欧拉矩阵中，当 cosp=0， sinp=1 的时候，也就是 pitch 角度等于 $\pi/2$ 时， E 变成了

$\begin{bmatrix} \cos r \cos h-\sin r\sin h & 0& \cos r\sin h + \sin r\cos h\\ \sin r \cos h+\cos r\sin h&0& \sin r\sin h - \cos r\cos h\\ 0&1&0\\ \end{bmatrix}$

$=\begin{bmatrix} \cos (r+h)&0& \sin (r+h)\\ \sin (r+h)&0&- \cos (r+h)\\ 0&1&0\\ \end{bmatrix}$ ,

该物体的旋转仅有r+h决定。然而我们仅确定了一个方向p的角度为90度，而物体仅有一个旋转物体，因此我们说该物体失去了一个方向上的自由度，也就是gimbal lock。

2.插值问题：由于欧拉角一般由矩阵计算，我们非常的难以进行两组欧拉角之间的插值。在两个矩阵之间进行矩阵的插值变换时非常繁琐的。可见欧拉角的局限性是非常严重的，因此我们提出另外一个概念，quaternion四元数。

Quaternion

quaternion 通过旋转轴和围绕这条旋转轴的角度来表示一次旋转。一般情况下相比于欧拉角，把旋转直接转换成quaternion 要比变成欧拉角便捷一些。而且,对于运动中的物体，例如摄像机旋转，很多时候都需要进行方向插值(orientation interpolation)，也就是在旋转的起点和终点进行插值来获得运动轨迹上每一点(像素点)的变化, 这时采用quaternion 要比欧拉角方便许多。

quaternion 的定义，一般写作 $\tilde{q}$ ，由实数部分和虚数部分组成。实数部分，一般写作 qw ,虚数部分一般写作 $q_{v}$ 。

我们有 $\tilde{q} = q_{v}+q_{w}$ ，

而虚数部分，又有

$q_{v} = iq_{x} +jq_{y} +kq_{z}$ ，

其中 $x, y, z$ 对应坐标系中 $x$ 轴 $y$ 轴 $z$ 轴。其中我们有

$i^{2}=j^{2}=k^{2} =-1$ ,

$jk = - kj = i$ ,

$ki = - ki = j$ ,

$ij = - ji = k$ $

这条性质很重要。我们在 $e u l er an g l e$ 和 $q u a t er ni o n$ 的变换中会用到。

另外，很多 $q u a t er ni o n$ 的乘法，加法，共轭等性质很容易查到，就不一一赘述了。

在这里重点只讲一条方便理解 $q u a t er ni o n$ 的性质， $\, quaternion$ ，也就是单位四元数。

$\, quaternion$ 可以写成

$(\sin\phi u_{q}, \cos\phi) = \sin\phi u_{q}+\cos\phi$

其中 $u_{q}$ 是三维单位向量，长度为 1 。因此，我们也有 $\tilde{q}$ 的长度等于

$\sqrt{\sin^{2}\phi(u_{q}\cdot u_{q})+\cos^{2}\phi}$

其中 $(u_{q}\cdot u_{q}) = 1$ ，因此有

$\sqrt{\sin^{2}\phi+\cos^{2}\phi}$

很好理解。

在单位向量中， $u_{q}$ 是旋转轴， $\phi$ 是旋转角的 1/2，如下图所示。

其中 $\sin\phi u_{q}$ 是虚数部分， $u_{q}$ 是虚数向量，也就是旋转轴， $\cos\phi$ 是实数部分。

三种旋转表示方法的基本性质就介绍到这里。作为开发者我们常常会遇到三种旋转表示方法之间的转化，以下将介绍三种旋转表示方法之间的转换。

2.Rotation Matrix，Euler Angle 和 Quaternion 之间的相互转换

Euler angle 和rotation matrix 之间的转化其实上文提过，代码直接照搬上述公式即可。

因为所有的 transform，无论是旋转还是平移，最终都要变成 4x4 矩阵代入到每个 vertex 的计算当中去，因此 quaternion 和 matrx44 之间的转换经常用到，所以先讲 quaternion 和 matrix4x4 之间的转化方法。

quaternion->matrix44 先上公式

$M_{q} = \begin{bmatrix} 1-s(q^{2}_{y}+q^{2}_{z})&s(q_{x}q_{y}-q_{w}q_{z})&s(q_{x}q_{z}+q_{w}q_{y})\\ s(q_{x}q_{y}+q_{w}q_{z})& 1-s(q^{2}_{x}+q^{2}_{z})&s(q_{y}q_{z}-q_{w}q_{x})\\ s(q_{x}q_{z}-q_{w}q_{y})&s(q_{y}q_{z}+q_{w}q_{x})&1-s(q^{2}_{x}+q^{2}_{y})\\ \end{bmatrix}$

其中 $s=2/(n(\tilde{q}))^{2}$ ，对于单位向量来说， n=1，所以 s=2，对于单位向量我们有

$M_{q} = \begin{bmatrix} 1-2(q^{2}_{y}+q^{2}_{z})&2(q_{x}q_{y}-q_{w}q_{z})&2(q_{x}q_{z}+q_{w}q_{y})\\ 2(q_{x}q_{y}+q_{w}q_{z})& 1-2(q^{2}_{x}+q^{2}_{z})&2(q_{y}q_{z}-q_{w}q_{x})\\ 2(q_{x}q_{z}-q_{w}q_{y})&2(q_{y}q_{z}+q_{w}q_{x})&1-2(q^{2}_{x}+q^{2}_{y})\\ \end{bmatrix}$

上代码：

matrix44 quaternion::toTransform() const {
	float xx = v.x * v.x, yy = v.y * v.y, zz = v.z * v.z;
	float xy = v.x * v.y, yz = v.y * v.z, xz = v.x * v.z;
	float wx = w * v.x, wy = w * v.y, wz = w * v.z;
	matrix44 ret = identity<matrix44, 4>();
	ret[0][0] = 1 - 2 * (yy + zz);
	ret[0][1] = 2 * (xy - wz);
	ret[0][2] = 2 * (xy + wy);
	ret[1][0] = 2 * (xy + wz);
	ret[1][1] = 1 - 2 * (xx + zz);
	ret[1][2] = 2 * (yz - wx);
	ret[2][0] = 2 * (xz - wy);
	ret[2][1] = 2 * (yz + wx);
	ret[2][2] = 1 - 2 * (xx + yy);
	return ret;
}

简单粗暴。

matrix4x4 -> quaternion:

首先重要的一点是计算 matrix 的 trace，也就是对角线之和，下面用 t 代替。

$\displaystyle t(M) = 4-2s(q^{2}_{x}+q^{2}_{y}+q^{2}_{z})=4(1-\frac{q^{2}_{x}+q^{2}_{y}+q^{2}_{z}}{q^{2}_{x}+q^{2}_{y}+q^{2}_{z}+q^{2}_{w}}) = \frac{4q^{2}_{w}}{q^{2}_{x}+q^{2}_{y}+q^{2}_{z}+q^{2}_{w}} = \frac{4q^{2}_{w}}{(n(\tilde{q}))^{2}}$

这样我们就得到了 $q_{w}$ 和 matrix trace 的关系，转化就方便多了，四条公式：

$\displaystyle q_{w} = \frac{1}{2}\sqrt{t(M)}$

$\displaystyle q_{x} = \frac{m_{21}-m_{12}}{4q_{w}}$

$\displaystyle q_{z} = \frac{m_{10}-m_{01}}{4q_{w}}$

上代码。

inline quaternion toQuaternion(const matrix44& mat) {
	float trace = mat[0][0] + mat[1][1] + mat[2][2] + mat[3][3];
	float qw = 1.f / 2 * sqrt(trace);
	float qx = (mat[2][1] - mat[1][2]) / (4 * qw);
	float qy = (mat[0][2] - mat[2][0]) / (4 * qw);
	float qz = (mat[1][0] - mat[0][1]) / (4 * qw);
  assert(trace > 0);
	quaternion ret;
	ret.w = qw;
	ret.v = vector3f(qx, qy, qz);
	return ret;
}

注意我这里是放在 header 文件里所以用了 inline。

对于设计和策划来说，欧拉角是一种更直接的表示方法，而对于开发者来说，quaternion 的计算更容易，所以两者的转换经常涉及到。

euler angle->quaternion:

对于欧拉角来说，三个方向，我们把每个方向的变换都转化为 quaternion，再按照旋转顺序相乘，我们就得到了最终的 quaternion。

对于

x-pitch 方向，我们有 $\tilde{q}_{x} = i\sin\alpha + \cos\alpha$ ,

y-head 方向，我们有 $\tilde{q}_{y} = j\sin\beta + \cos\beta$ ,

z-roll 方向，我们有 $\tilde{q}_{z} = k\sin\gamma + \cos\gamma$

按照 $E (h e a d, p i t c h, ro ll)$ 的方向相乘， $R_{z} \cdot R_{x} \cdot R_{y}$ , 得到

$(\cos \frac{\gamma}{2}+\sin\frac{\gamma}{2}k)(\cos \frac{\alpha}{2}+\sin\frac{\alpha}{2}i)(\cos \frac{\beta}{2}+\sin\frac{\beta}{2}j)$

此时注意乘法的方向，从后往前，根据最开始提到的 quaternion 的基本性质，化简得到：

$(\cos\frac{\gamma}{2}\cos\frac{\alpha}{2}\cos\frac{\beta}{2} + \sin\frac{\gamma}{2}\sin\frac{\alpha}{2}\sin\frac{\beta}{2}) +$

$(\cos\frac{\gamma}{2}\sin\frac{\alpha}{2}\cos\frac{\beta}{2} - \sin\frac{\gamma}{2}\cos\frac{\alpha}{2}\sin\frac{\beta}{2})i +$

$(\cos\frac{\gamma}{2}\cos\frac{\alpha}{2}\sin\frac{\beta}{2} + \sin\frac{\gamma}{2}\sin\frac{\alpha}{2}\cos\frac{\beta}{2})j +$

$(\cos\frac{\gamma}{2}\sin\frac{\alpha}{2}\sin\frac{\beta}{2} + \sin\frac{\gamma}{2}\sin\frac{\alpha}{2}\cos\frac{\beta}{2})k$

这样一个 quaternion 的 $q_w$ ， $q_x$ ， $q_y$ ， $q_z$ 就对应得到了。如果你用到的不同的 $h, p, r$ 方向，那么对应的结果就会不一样，应该重新计算。

上代码：

quaternion::quaternion(const eulerAngle& ea) {
	float cosa, sina, cosb, sinb, cosg, sing;
	cosa = std::cos(ea.pitch / 2.f);
	sina = std::sin(ea.pitch / 2.f);
	cosb = std::cos(ea.head / 2.f);
	sinb = std::sin(ea.head / 2.f);
	cosg = std::cos(ea.roll / 2.f);
	sing = std::sin(ea.roll / 2.f);
	w = cosg * cosa * cosb + sing * sina * sinb;
	v.x = cosg * sina * cosb - sing * cosa * sinb;
	v.y = cosg * cosa * sinb + sing * sina * cosb;
	v.z = cosg * sina * sinb + sing * cosa * cosb;
}

quaternion->euler angle:

这里我们要用到欧拉变换里的公式：

$\begin{bmatrix} \cos r \cos h-\sin r\sin p\sin h & -\sin r\cos p& \cos r\sin h + \sin r\sin p\cos h\\ \sin r \cos h+\cos r\sin p\sin h & \cos r\cos p& \sin r\sin h - \cos r\sin p\cos h\\ -\cos p\sin h&\sin p& \cos p\cos h\\ \end{bmatrix}$

在这个矩阵中，很容易得到

$\tan h= -\frac{E01}{E11}$ ，

$\tan h = -\frac{E20}{E22}$ ，

$\sin p = E21$ 。

所以直接通过反三角函数就可以求得其中的值。这里注意，由于 $\arcsin$ 定义域的关系，p 角只能确定从 -90° 到 90° 之间。

上代码：

eulerAngle::eulerAngle(const quaternion& q) {
	float x = q.v.x, y = q.v.y, z = q.v.z, w = q.w;
	float e20 = 2.0f * (x * z - w * y);
	float e22 = 1.0f - 2.0f * (x * x + y * y);
	head = std::atan2(-e20, e22);
	float e21 = 2 * (y * z + w * x);
	e21 = e21 > 1.0f ? 1.0f : e21;
	e21 = e21 < -1.0f ? -1.0f : e21;
	pitch = std::asin(e21);
	float e01 = 2.0f * (x * y - w * z);
	float e11 = 1.0f - 2.0f * (x * x + z * z);
	roll = std::atan2(-e01, e11);
}

这里我们跑一跑，确定转换关系是否正确：

eulerAngle ea(0.2f, 0.4f, 1.0f);
quaternion q(ea);
eulerAngle test(q);
std::cout << test << std::endl;

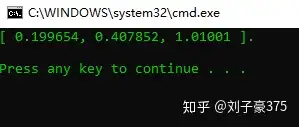
没问题，误差可以接受。

总结

以上就是关于旋转矩阵，欧拉变换和四元数组的基本概念和转换关系的全部内容。

发布于 2020-03-30 23:21

via:

彻底搞懂 “旋转矩阵 / 欧拉角 / 四元数”，让你体会三维旋转之美_欧拉角判断动作 - CSDN 博客 肥肥胖胖是太阳已于 2022-02-14 14:14:22 修改
https://blog.csdn.net/weixin_45590473/article/details/122884112
四元数、欧拉角、旋转矩阵、旋转向量之间的转换_欧拉旋转定理-CSDN博客 泠山已于 2024-04-11 16:33:55 修改
https://blog.csdn.net/qq_28087491/article/details/122830550
python 实现四元数、欧拉角、旋转矩阵、旋转向量的相互转换-CSDN博客 大大大管的笔记本已于 2023-07-19 11:47:14 修改
https://blog.csdn.net/cg1135217680/article/details/130105937
图像引擎里的旋转变换–Euler Angle&Quaternion - 知乎 刘子豪375 发布于 2020-03-30 23:21
https://zhuanlan.zhihu.com/p/120312829