什么是刚体运动以及三维空间中刚体运动描述方式有哪些?
两个坐标系之间的运动由一个旋转加上一个平移组成,这种运动称为刚体运动。描述三维空间中刚体运动的方式有旋转矩阵、旋转向量、欧拉角、四元数。
请描述左手坐标系和右手坐标系。
大拇指——y
食指——z
中指——x

内积和外积的公式和对应的几何意义
内积公式:

内积几何意义:
1.两个向量之间的夹角
2.b向量在a向量方向上的投影
外积公式:
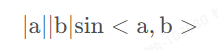
外积几何意义:
1.在三维几何中,两个向量的外积结果是一个向量,该向量垂直于这两个向量构成的平面,也称法向量。
2.在二维空间中,外积在数数值上等于两个向量构成的平行四边形的面积。
定义坐标系1、坐标系2,向量a在两个坐标系下的坐标是a1,a2,用欧式变化表达两者之间的关系。
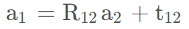
什么是齐次坐标,为什么要引入它?
齐次坐标系,就是用N+1维向量(矩阵)来表示N维向量(矩阵)。这里引入齐次坐标,是因为这样吧三维向量末尾加1,变成4维向量后,就可以把旋转和平移写在一个矩阵里,得到变换矩阵T。左上角是旋转矩阵,右上角是平移向量,左下角是0向量,右下角是1。
旋转矩阵描述刚体运动的缺点
1.旋转矩阵是3*3有9个量,而一次旋转只有3个自由度,这样的表达是冗余的。
2.旋转矩阵带有约束,必须是正交矩阵且行列式为1,这些约束会使得求解变得困难。
什么是旋转向量?
任意的旋转都可以用旋转轴和旋转角来刻画,使用一个向量,使得向量的方向与旋转轴一致,长度为旋转角。这种向量是旋转向量。
旋转矩阵和旋转向量之间的关系?
已知一个旋转矩阵R,一个旋转向量,旋转向量的单位向量为n,角度为(长度)Θ,从旋转向量之到旋转矩阵的转换过程由罗德里格斯公式表明:
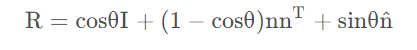
用Eigen实现旋转向量和旋转矩阵之间的转换。
# 向量和旋转向量是不一样的,向量的base是Eigen::Matrix,而旋转向量是Eigen::AngleAxis
# 初始化旋转向量
Eigen::AngleAxisd rotation_vector(M_PI / 2, Eigen::Vector3d(1,2,3).normalized());
# 注意normalized()返回向量,norm返回L2范数,normalize()是归一化处理,不返回值
# 旋转向量转旋转矩阵
Eigen::Matrix3d rotation_matrix = rotation_vector.matrix();
# 旋转矩阵转旋转向量
Eigen::Vector3d rotate;
rotate.fromRotationMatrix(rotation_matrix);
什么是欧拉角,它的重大缺点?
无论是旋转矩阵还是旋转向量,虽然能描述旋转,但是对人类来说很不直观。欧拉角提供了一种非常直观的方式来描述旋转——使用3个分离的转角,把一个旋转分解成3次不同的旋转。假设一个刚体的前方为x轴,右侧为Y轴,上方为Z轴。通常使用ypr(yaw-pitch-row)旋转顺序。
yaw——绕物体的z轴旋转得到偏航角yaw;
pitch——绕旋转后的y轴旋转得到俯仰角pitch;
row——绕旋转之后的x轴旋转得到滚转角roll。
什么是万向锁?
在俯仰角为正负90度时,第一次旋转和第三次旋转将使用同一个轴,使得系统丢失了一个自由度。这就是万象锁问题,也称为奇异性问题。
为什么要引入四元数,四元数是什么?
旋转矩阵表示冗余,欧拉角和旋转向量是紧凑的单具有奇异性。而四元数既是紧凑的又没有奇异性。三维旋转可以由单位四元数来描述,一个四元数拥有一个实部和三个虚部。
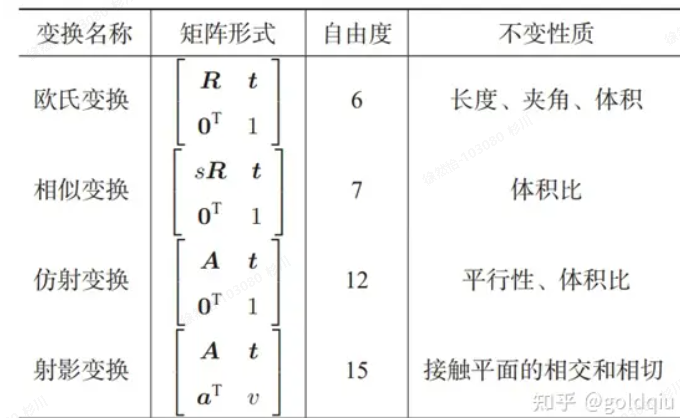
写出相似变换、仿射变换、射影变换的矩阵形式。





















 282
282











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








