0.题外话
虽然本篇文章涉及的概念和题目侧重电磁侧信道攻击的出题,但是为了照顾到零基础的读者,还是需要先从侧信道攻击的概念和分类进行讲解,后续的出题指南(如果还有续集)将不再详细阐述相关概念,会在出题的时候将本篇文章嵌入其中供零基础和新关注的粉丝阅读。本篇文章较长,若对各位有所帮助,点赞爱心在看一键三连走起来,在此谢过啦。若能转发到朋友圈和各大技术交流群拍砖我那就更好啦。
本次出题指南共计有五道电磁攻击的题目,从易到难涉及的概念有基础电磁攻击、电磁攻击和单位格基的结合,电磁攻击和随机格基的结合、电磁攻击和chacha20的结合,最后一道题参考了2024年美密顶会论文Adaptively Sound Zero-Knowledge SNARKs for UP当中的零知识证明及LWE的部分理论,可以说是非常丰富了。
言归正传,我们开始吧。
1.什么是侧信道攻击
1.1.概述
侧信道攻击属于密码学的物理攻击(Physical Attack)范畴,是密码学中的一个重要分支。这种攻击利用计算设备在执行密码算法时泄露的物理信息,如功耗、时间、电磁辐射、声波等,来推测内部的秘密数据(如密钥)。与传统的密码分析不同,侧信道攻击并不直接针对算法的数学结构,而是利用实现过程中不可避免的物理信息泄漏。
1.2.侧信道攻击的起源与发展
侧信道攻击的概念起源于20世纪90年代末。1996年,保罗·科彻(Paul Kocher)发表了关于时序攻击(Timing Attacks)的论文,揭示了通过测量加密操作的执行时间来推断密钥信息的可能性。这标志着侧信道攻击研究的开端。随后,他与他人合作,提出了差分功耗分析(Differential Power Analysis, DPA),这进一步推动了侧信道攻击的研究和发展。
1.3.侧信道攻击的详细分类及介绍
侧信道攻击是通过分析加密设备在执行操作时泄漏的物理信息来获取敏感数据的技术。以下是侧信道攻击的几种主要类型及其详细介绍:
1.3.1功耗分析攻击(Power Analysis Attacks)
功耗分析攻击通过测量设备在执行加密操作时消耗的电力来获取信息。这类攻击分为简单功耗分析(SPA)和差分功耗分析(DPA)。
简单功耗分析(Simple Power Analysis, SPA)
原理:SPA利用设备在执行不同操作时功耗变化的直接观测。攻击者可以通过观察这些变化,推断出加密过程中具体操作的类型和顺序。例如,在执行加密算法时,设备在处理不同数据位时的功耗可能会有所不同。
举例:假设一个设备在处理二进制“1”时消耗的功率比处理“0”时高。通过观察功耗图,可以推断出每一位是“1”还是“0”,从而推断出整个密钥。
差分功耗分析(Differential Power Analysis, DPA)
原理:DPA更加复杂和强大。攻击者收集大量功耗曲线,并利用统计方法分析功耗数据中的微小差异。通过对这些差异进行统计处理,攻击者可以找出与密钥相关的信息。
举例:攻击者可以使用数千次加密操作的功耗数据,计算每次操作的平均功耗。然后,通过对不同密钥假设下的功耗进行统计比较,找到最有可能的密钥。
1.3.2.电磁分析攻击(Electromagnetic Analysis, EMA)
电磁分析攻击通过测量设备在执行操作时产生的电磁辐射来获取信息。这类攻击分为简单电磁分析(SEMA)和差分电磁分析(DEMA)。
简单电磁分析(Simple Electromagnetic Analysis, SEMA)
原理:SEMA类似于SPA,利用设备在执行不同操作时产生的电磁辐射变化来获取信息。攻击者通过观察这些变化,推断出加密过程中具体操作的类型和顺序。
举例:通过在设备附近放置一个电磁探头,攻击者可以记录设备在执行加密操作时产生的电磁信号。通过分析这些信号的强度和频率变化,可以推断出密钥信息。
差分电磁分析(Differential Electromagnetic Analysis, DEMA)
原理:DEMA类似于DPA,通过收集大量电磁辐射数据,并利用统计方法分析其中的微小差异。通过对这些差异进行统计处理,攻击者可以找出与密钥相关的信息。
举例:攻击者收集数千次加密操作的电磁辐射数据,通过统计方法比较不同密钥假设下的电磁信号,找到最有可能的密钥。
1.3.3.时序攻击(Timing Attacks)
时序攻击通过测量设备在执行操作时所需的时间来获取信息。
原理:不同的操作或相同操作处理不同数据所需的时间可能不同。攻击者可以通过测量这些时间差异,推断出内部操作细节和密钥信息。
举例:某些加密算法的执行时间取决于输入数据和密钥。通过多次测量加密操作的执行时间,攻击者可以推断出密钥的某些部分。例如,RSA加密算法中的模幂运算时间可能会泄露关于密钥的信息。
1.3.4.缓存攻击(Cache Attacks)
缓存攻击通过分析处理器缓存的行为来获取信息。
原理:加密算法在执行过程中会访问缓存,不同数据访问模式会导致不同的缓存命中率和访问时间。攻击者可以通过分析这些访问模式,推断出密钥信息。
举例:一个常见的缓存攻击是“Prime+Probe”攻击。攻击者首先将自己的数据加载到缓存中,然后让加密算法运行。通过测量加密算法运行后自己数据的访问时间,攻击者可以推断出加密算法访问缓存的模式,从而推断出密钥。
1.3.5.声学攻击(Acoustic Attacks)
声学攻击通过分析设备在执行操作时产生的声波来获取信息。
原理:不同操作可能会产生不同的声音模式,攻击者可以通过测量和分析这些声音,推断出内部操作和密钥信息。
举例:某些设备在执行不同的加密操作时会产生不同频率或强度的声音。通过使用麦克风记录这些声音,并进行频谱分析,攻击者可以推断出加密操作的类型和密钥。
1.3.6.光学攻击(Optical Attacks)
光学攻击通过观察设备的光学辐射(如LED指示灯的闪烁)来获取信息。
原理:设备在执行不同操作时可能会发出不同的光学信号。攻击者可以通过测量这些光信号的变化,推断出内部操作和密钥信息。
举例:某些设备的LED指示灯在执行加密操作时可能会闪烁不同的模式。通过使用高速摄像设备记录这些闪烁模式,并进行分析,攻击者可以推断出加密操作的类型和密钥。
2.侧信道攻击的防御
为了防御侧信道攻击,可以采取多种技术和策略,包括但不限于:
2.1.掩码技术(Masking)
原理:在计算过程中引入随机掩码,使得泄露的信息与实际密钥无关。即使攻击者获得了侧信道信息,也无法直接推断出密钥。
具体措施:在加密过程中,使用随机数对密钥进行掩码处理,使得功耗、时间或其他物理特征不再直接与密钥相关联。
2.2.均衡功耗技术(Balancing Power Consumption)
原理:通过设计电路和算法,使得不同操作消耗的功率尽可能一致,从而减少功耗分析的有效性。
具体措施:设计硬件电路时,确保所有加密操作的功耗变化保持在一个固定范围内,避免特定操作的功耗差异过大。
2.3.时间均衡技术(Balancing Timing)
原理:确保所有操作的执行时间尽可能一致,防止时序攻击。
具体措施:通过添加伪随机延迟或固定所有操作的执行时间,使得攻击者无法通过时间测量推断出密钥信息。
2.4.噪声引入(Noise Injection)
原理:在侧信道信号中引入随机噪声,增加攻击者提取有用信息的难度。
具体措施:在加密设备的输出中添加随机噪声信号,使得实际操作的物理特征被噪声掩盖。
2.5.硬件防护(Hardware Countermeasures)
原理:通过设计更安全的硬件架构,如使用电磁屏蔽和物理隔离,来减少侧信道信息的泄漏。
具体措施:在芯片设计中加入电磁屏蔽层,减少电磁辐射泄漏;通过物理隔离技术,降低功耗和时序信息的外部可观测性。
3.电磁侧信道攻击
电磁侧信道攻击(Electromagnetic Analysis, EMA)是通过测量设备在执行操作时产生的电磁辐射来获取信息的攻击技术。这种攻击利用设备在运行过程中不可避免的电磁辐射泄漏,通过分析这些电磁信号,攻击者可以推断出设备内部的操作和密钥信息。
3.1.电磁侧信道攻击的原理
电磁侧信道攻击分为简单电磁分析(SEMA)和差分电磁分析(DEMA):
简单电磁分析(Simple Electromagnetic Analysis, SEMA)
原理:SEMA通过直接观察设备在执行不同操作时产生的电磁辐射变化来获取信息。不同操作的电磁辐射特征不同,通过识别这些特征,攻击者可以推断出加密过程中具体操作的类型和顺序。
步骤:
使用电磁探头在设备附近记录电磁信号。
分析电磁信号,识别出特定操作产生的特征。
基于已知操作的电磁特征,推断出密钥信息。
差分电磁分析(Differential Electromagnetic Analysis, DEMA)
原理:DEMA通过统计方法分析大量电磁辐射数据中的微小变化。与差分功耗分析(DPA)类似,DEMA利用统计方法找出电磁辐射数据与密钥之间的相关性。
步骤:
-
执行大量的加密操作,并记录每次操作的电磁辐射信号。
-
对每次加密操作的输入和电磁辐射信号进行分组处理,根据不同的密钥假设计算各组电磁辐射信号的差异。
-
统计分析各组电磁辐射信号的差异,找出与实际密钥相关的假设。

3.2.原理涉及到的公式
3.2.1电磁信号的生成模型
假设设备在执行加密操作时,产生的电磁信号是输入数据
x
x
x和密钥
k
k
k的函数,可以表示为:
S
=
f
(
x
,
k
)
+
N
S = f(x, k) + N
S=f(x,k)+N
其中:
- S S S是设备产生的电磁信号。
- f ( x , k ) f(x, k) f(x,k) 是信号生成函数,依赖于输入数据 x x x和密钥 k k k。
- N N N是噪声信号,通常假设为高斯噪声。
3.2.2.相关性分析
DEMA 的核心在于通过统计方法分析电磁信号与假设密钥之间的相关性。假设我们有 n n n个输入数据样本 x i ( i = 1 , 2 , … , n ) x_i( i = 1, 2, \ldots, n) xi(i=1,2,…,n),以及对应的电磁信号 S i S_i Si。
对于每个密钥猜测 $k’ $,我们可以计算假设信号:
S ^ i = f ( x i , k ′ ) \hat{S}_i = f(x_i, k') S^i=f(xi,k′)
然后,计算实际信号 S i S_i Si与假设信号 S ^ i \hat{S}_i S^i 的相关系数 ρ ( k ′ ) \rho(k') ρ(k′):
ρ ( k ′ ) = ∑ i = 1 n ( S i − S ˉ ) ( S ^ i − S ^ ˉ ) ∑ i = 1 n ( S i − S ˉ ) 2 ∑ i = 1 n ( S ^ i − S ^ ˉ ) 2 \rho(k') = \frac{\sum_{i=1}^{n} (S_i - \bar{S})(\hat{S}_i - \bar{\hat{S}})}{\sqrt{\sum_{i=1}^{n} (S_i - \bar{S})^2 \sum_{i=1}^{n} (\hat{S}_i - \bar{\hat{S}})^2}} ρ(k′)=∑i=1n(Si−Sˉ)2∑i=1n(S^i−S^ˉ)2∑i=1n(Si−Sˉ)(S^i−S^ˉ)
其中:
S
ˉ
\bar{S}
Sˉ 是实际信号
S
i
S_i
Si 的平均值。
S
^
ˉ
\bar{\hat{S}}
S^ˉ是假设信号
S
^
i
\hat{S}_i
S^i的平均值。
相关系数 ρ ( k ′ ) \rho(k') ρ(k′) 反映了实际信号与假设信号的相似程度。假设密钥 $k’ $越接近真实密钥 k k k,相关系数 ρ ( k ′ ) \rho(k') ρ(k′)越大。
3.2.3.差分电磁分析的步骤
-
收集电磁信号:记录设备在执行大量加密操作时产生的电磁信号 S i S_i Si。
-
生成假设信号:对于每个密钥猜测 k ′ k' k′,生成假设信号 S ^ i \hat{S}_i S^i。
-
计算相关系数:计算实际信号 S i S_i Si 与假设信号 S ^ i \hat{S}_i S^i之间的相关系数 ρ ( k ′ ) \rho(k') ρ(k′)。
-
确定密钥:找出使相关系数 ρ ( k ′ ) \rho(k') ρ(k′) 最大的密钥猜测 k ′ k' k′,即为预测的密钥。
以下是一个模拟电磁侧信道攻击的简单示例。该示例包括生成模拟电磁信号数据,并使用差分电磁分析(DEMA)来推断密钥信息。我们将使用NumPy生成和处理数据,并将生成的数据保存为.npy格式文件。
首先,我们生成生成了模拟的输入数据和对应的电磁信号数据。输入数据 input_data 包含1000个样本,每个样本的电磁信号 signals 的长度为500。。假设我们有一个简单的加密算法,每次加密操作产生的电磁信号是加密输入和密钥的函数。我们将利用差分电磁分析(DEMA)方法来推断密钥信息
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import butter, lfilter, freqz
input_data = np.load('input_data.npy')
signals = np.load('signals.npy')
def butter_lowpass(cutoff, fs, order=5):
nyquist = 0.5 * fs
normal_cutoff = cutoff / nyquist
b, a = butter(order, normal_cutoff, btype='low', analog=False)
return b, a
def butter_lowpass_filter(data, cutoff, fs, order=5):
b, a = butter_lowpass(cutoff, fs, order=order)
y = lfilter(b, a, data)
return y
order = 6
fs = 1000.0
cutoff = 30.0
filtered_signals = np.array([butter_lowpass_filter(signal, cutoff, fs, order) for signal in signals])
print("Filtered Signals Shape:", filtered_signals.shape)
def differential_electromagnetic_analysis(input_data, signals, key_guesses):
correlations = np.zeros(len(key_guesses))
for key_guess in key_guesses:
hypothetical_signals = np.array([np.sin(data + key_guess) for data in input_data])
correlation = np.array([np.corrcoef(signals[:, i], hypothetical_signals)[0, 1] for i in range(signal_length)])
correlations[key_guess] = np.mean(correlation)
return correlations
correlations = differential_electromagnetic_analysis(input_data, filtered_signals, key_guesses)
predicted_key = key_guesses[np.argmax(correlations)]
print(f'Predicted Key: {predicted_key}')
plt.plot(key_guesses, correlations)
plt.xlabel('Key Guesses')
plt.ylabel('Correlation')
plt.title('Differential Electromagnetic Analysis with Filtered Signals')
plt.show()
plt.figure()
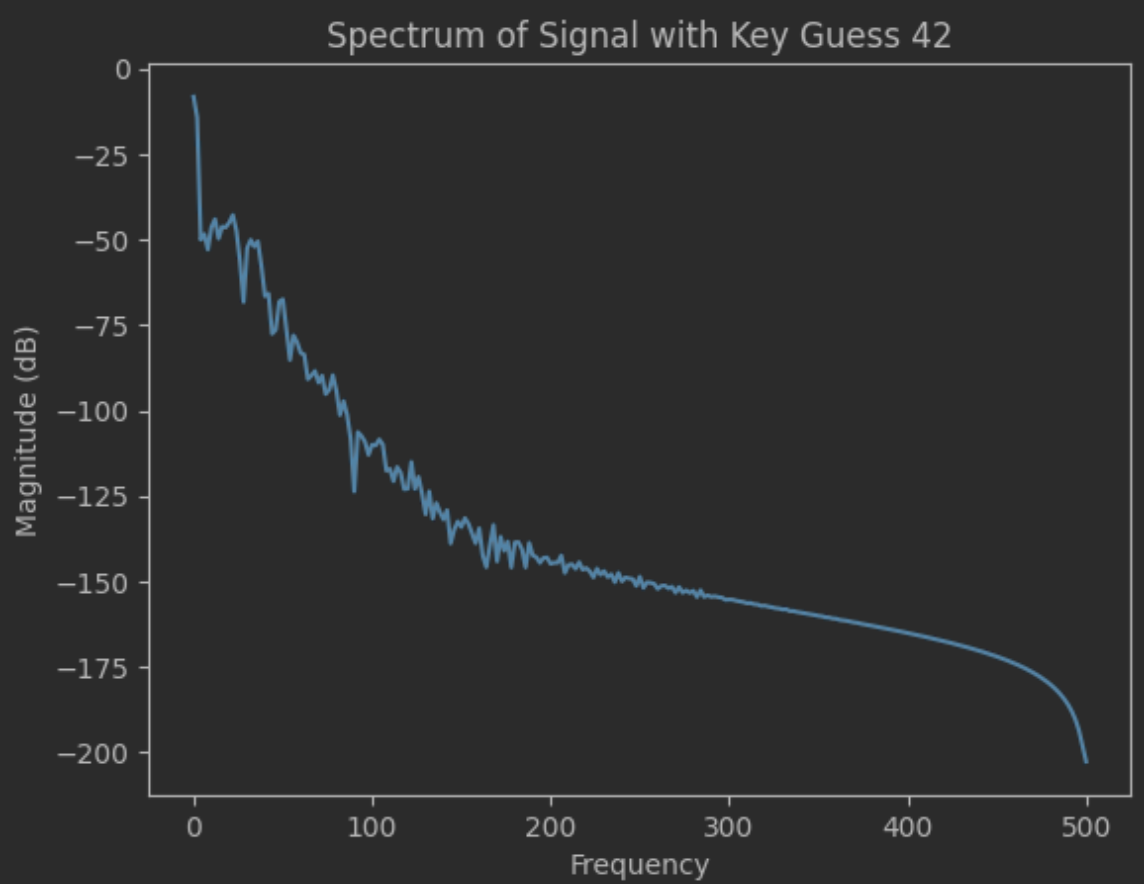
plt.magnitude_spectrum(filtered_signals[np.argmax(correlations)], Fs=fs, scale='dB')
plt.title(f'Spectrum of Signal with Key Guess {predicted_key}')
plt.show()
因为我在生成的数据里加入了噪声,那为什么要有噪声,这是因为电磁信号中通常包含高频噪声,这些噪声可能会干扰信号的有效部分,使得信号分析更加困难。低通滤波器可以有效地抑制这些高频噪声,提取出信号的有效部分。还有就是低通滤波器可以平滑信号,使其波动减小,更容易识别信号中的特征。例如,在差分电磁分析(DEMA)中,平滑的信号有助于提高相关性计算的精度。巴特沃斯滤波器是一种具有平坦频率响应的滤波器,即在通带内没有波纹,这使得它在保持信号特征的同时有效地抑制噪声。的设计目标是实现最平坦的通带响应,没有波动,这在处理侧信道信号时非常有用,因为它不会引入额外的波动或失真。巴特沃斯低通滤波器是一种平滑滤波器,旨在尽可能地保持信号的低频成分,同时去除高频噪声。其频率响应是“最平坦”的,没有通带波纹。
滤波器设计:
阶数(Order):滤波器的阶数决定了其陡峭程度。阶数越高,滤波器的过渡带越陡。
截止频率(Cutoff Frequency):决定了滤波器开始衰减信号的频率。
巴特沃斯滤波器的传递函数为:
H
(
s
)
=
1
1
+
(
s
/
ω
c
)
2
n
H(s) = \frac{1}{\sqrt{1 + (s / \omega_c)^{2n}}}
H(s)=1+(s/ωc)2n1
其中:
- s s s 是复频率变量。
- ω c \omega_c ωc 是截止频率。
- n n n 是滤波器的阶数。
在以上的代码里使用巴特沃斯低通滤波器对信号进行了滤波,参数如下:
- 采样频率(fs):1000 Hz
- 截止频率(cutoff):30 Hz
- 滤波器阶数(order):6

1.生成假设信号:对于每个密钥猜测 k ′ k' k′,计算假设信号 S ^ i = sin ( x i + k ′ ) \hat{S}_i = \sin(x_i + k') S^i=sin(xi+k′)。
2.计算相关系数:对于每个信号样本点 i i i,计算实际信号 S i S_i Si 与假设信号 S ^ i \hat{S}_i S^i之间的相关系数 ρ ( k ′ ) \rho(k') ρ(k′)。
3.累计相关性:将所有信号样本点的相关性累计,以获得每个密钥猜测的总相关性。
4.确定密钥:找出总相关性最大的密钥猜测 k ′ k' k′,即为预测的密钥。
通过上述步骤,我们可以有效地利用电磁侧信道攻击技术来推测设备的密钥信息。预处理步骤中的滤波处理。使用巴特沃斯低通滤波器,可以显著提高信号的质量,从而提高分析的准确性和效率。理解这些原理和步骤,有助于更深入地掌握侧信道攻击技术。
4.出题指南
本环节总计5道题,由易到难,均有出题思路及解题过程。
4.1.test_easy_flag
这道题目要求通过信号处理和分析技术,从模拟的电磁信号中提取隐藏的信息(flag)
4.1.1.出题思路
- 信号生成和处理:
通过生成包含随机噪声的正常信号 normal_signal,模拟实际电磁信号的复杂性。
设计插入信息 flag 的机制,将其转换为二进制并以高低幅度表示,从而在信号中嵌入信息。
- 信号插入:
选择信号的某个位置(如5000)插入 flag_signal,确保信息混杂在正常信号中。
- 数据保存和提取:
将生成的信号保存为 .npy 文件,便于之后加载和分析。
设计从信号中提取信息的过程,验证信息提取的准确性。
- 信号可视化:
绘制包含flag信息的信号图,帮助观察信号特征和信息插入的效果。
这道题目有两个文件,一个是包含了flag信息在内的电磁信号数据文件,再一个是频谱图。


4.1.2.解题思路

- 首先观察频谱图
频谱图展示了信号在不同频率下的能量分布。在嵌入flag信息的区域,信号的幅度显著增加,形成了明显的峰值。
频谱图中的这些峰值提供了一个明确的视觉线索,使我们能够识别出信号中的异常部分,并确定flag信息插入的位置。
通过频谱图,可以验证信号处理中检测到的异常是否与实际嵌入的信息相对应。
- 读取信号数据:
从保存的.npy文件中读取包含flag信息的信号数据。这一步是为了获取我们要分析的信号数据。
- 检测信号异常:
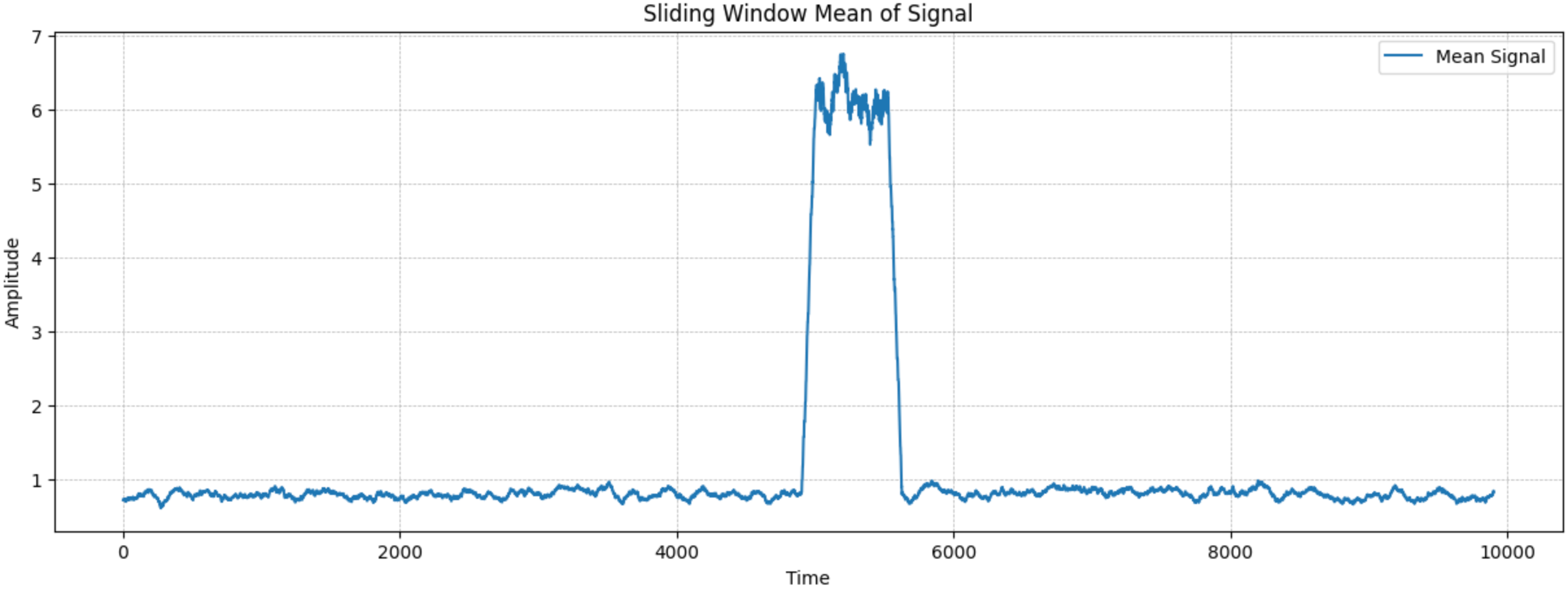
使用滑动窗口计算信号的平均值。滑动窗口是一种常用的平滑技术,通过将窗口内的信号取平均值,能够突出显示信号中的显著变化部分。
通过滑动窗口计算后的信号平均值,可以观察到信号中的异常部分。这些异常部分可能是由于嵌入了flag信息所导致的。
绘制滑动平均后的信号图,从图中手动确定异常信号段的起始位置。通过观察图形来确定异常信号的起始位置。
- 提取异常信号段:
根据观察到的起始位置提取异常信号段。假设flag的长度未知,先取一个足够长的段作为示例进行分析。
提取信号段后,可以进一步处理和分析该信号段,以便恢复其中的嵌入信息。
- 分析高幅度和低幅度值:
提取的信号段中包含高幅度和低幅度的信号,这些信号分别表示二进制的1和0。
通过统计方法估计高幅度和低幅度值。例如,可以使用95百分位数作为高幅度的估计,5百分位数作为低幅度的估计。
计算用于区分0和1的阈值。通常情况下,可以取高幅度和低幅度的平均值作为阈值。
- 恢复二进制信息:
使用估计的阈值,将提取段的信号转换为二进制信息。即,信号幅值大于阈值的部分判定为1,信号幅值小于阈值的部分判定为0。
通过这一过程,可以得到flag信息的二进制表示。
- 将二进制信息转为字符串:
将二进制信息按每8位一组转换为字符。每8位二进制表示一个ASCII字符。
将所有的二进制组转换为字符后,组合成完整的字符串,恢复原始的flag信息。
import numpy as np
import matplotlib.pyplot as plt
signal_with_flag = np.load('test_easy_flag.npy')
window_size = 100 # 滑动窗口大小
signal_mean = np.convolve(np.abs(signal_with_flag), np.ones(window_size)/window_size, mode='valid')
plt.figure(figsize=(15, 5))
plt.plot(signal_mean, label='Mean Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Sliding Window Mean of Signal')
plt.legend()
plt.show()
start_index = 5000
flag_length = 800
extracted_flag_signal = signal_with_flag[start_index:start_index + flag_length]
plt.figure(figsize=(15, 5))
plt.plot(extracted_flag_signal, label='Extracted Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Extracted Signal for Analysis')
plt.legend()
plt.show()
high_amplitude = np.percentile(extracted_flag_signal, 95)
low_amplitude = np.percentile(extracted_flag_signal, 5)
threshold = (high_amplitude + low_amplitude) / 2
print(f"Estimated high_amplitude: {high_amplitude}")
print(f"Estimated low_amplitude: {low_amplitude}")
print(f"Threshold for binary decision: {threshold}")
recovered_flag_binary = ''.join(['1' if np.mean(np.abs(extracted_flag_signal[i])) > threshold else '0'
for i in range(flag_length)])
recovered_flag = ''.join([chr(int(recovered_flag_binary[i:i+8], 2))
for i in range(0, len(recovered_flag_binary), 8)])
print("Recovered Flag:", recovered_flag)

代码运行后可获得flag:Estimated high_amplitude: 11.11855406375027
Estimated low_amplitude: -0.8942447179527468
Threshold for binary decision: 5.112154672898762
Recovered Flag: flag{To_be_both_a_speaker_of_words_and_a_doer_of_deeds_xuruihan_is_the_author}

4.1.3代码分析
- 导入必要的库:
import numpy as np
import matplotlib.pyplot as plt
numpy 用于数值计算。
matplotlib.pyplot 用于绘制图形。
- 读取信号数据:
signal_with_flag = np.load('test_easy_flag.npy')
从文件中加载包含flag信息的信号数据。
- 检测信号异常:
window_size = 100
signal_mean = np.convolve(np.abs(signal_with_flag), np.ones(window_size)/window_size, mode='valid')
使用滑动窗口计算信号的平均值,以检测信号中的异常部分。
- 确定异常信号段起始位置:
start_index = 5000
手动确定异常信号段的起始位置。
- 提取异常信号段:
flag_length = 800
extracted_flag_signal = signal_with_flag[start_index:start_index + flag_length]
提取包含flag信息的信号段。
- 分析高幅度和低幅度值:
high_amplitude = np.percentile(extracted_flag_signal, 95)
low_amplitude = np.percentile(extracted_flag_signal, 5)
threshold = (high_amplitude + low_amplitude) / 2
通过统计分析估计高幅度和低幅度值,并计算用于区分0和1的阈值。
- 打印估计的高低幅度和阈值:
print(f"Estimated high_amplitude: {high_amplitude}")
print(f"Estimated low_amplitude: {low_amplitude}")
print(f"Threshold for binary decision: {threshold}")
输出估计的高幅度、低幅度和阈值。
- 恢复二进制信息:
recovered_flag_binary = ''.join(['1' if np.mean(np.abs(extracted_flag_signal[i])) > threshold else '0'
for i in range(flag_length)])
根据阈值将提取的信号段转换为二进制信息。
- 将二进制信息转为字符串:
recovered_flag = ''.join([chr(int(recovered_flag_binary[i:i+8], 2))
for i in range(0, len(recovered_flag_binary), 8)])
将二进制信息按每8位一组转换为ASCII字符,恢复原始的flag信息。
- 打印恢复的flag:
print("Recovered Flag:", recovered_flag)
输出恢复的flag。
- 绘制信号图:
plt.figure(figsize=(15, 5))
plt.plot(signal_mean, label='Mean Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Sliding Window Mean of Signal')
plt.legend()
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()
绘制滑动窗口均值图。
- 绘制提取的信号段图:
plt.figure(figsize=(15, 5))
plt.plot(extracted_flag_signal, label='Extracted Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Extracted Signal for Analysis')
plt.legend()
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()
绘制提取的信号段图。
4.2.easy_geji
题目通过模拟电磁信号插入flag信息,并从中提取该信息,主要考察对信号处理、格基插入与提取、以及数据编码和解码的理解与应用。
4.2.1.出题思路
- 基础知识:
通过定义和转换flag信息,考察对字符串编码和二进制处理的理解。
使用格基矩阵(简单的单位矩阵)展示基本线性代数概念的应用。
- 信号处理:
通过生成随机信号并插入信息,考察对信号生成和处理的能力。
通过滑动窗口检测异常信号段,考察信号异常检测的应用。
- 数据提取与校验:
提取并校验嵌入信号中的信息,考察对信号提取和数据校验的综合应用能力。
- 可视化:
通过绘制矩阵和信号图,考察数据可视化能力。
这道题目有三个文件,一个是包含了flag信息和单位格基矩阵在内的电磁信号数据文件,一个是单位矩阵图,再一个是频谱图。



4.2.2.解题思路
首先观察图10和图11,单位矩阵作为简单的格基矩阵用于插入和恢复信号中的信息。
图10通过单位矩阵,可以将高维数据映射到格点上,从而实现数据的嵌入和提取。
图11滑动窗口均值图能够清晰地识别出包含flag信息的异常信号段的起始和结束位置。在本例中,异常信号段的起始位置大约为5000。
- 读取信号数据:
从保存的.npy文件中读取包含flag信息的信号数据。该步骤是为了获取要分析的信号数据。
- 检测信号异常:
使用滑动窗口计算信号的平均值,以检测信号中的异常部分。滑动窗口是一种常用的平滑技术,通过将窗口内的信号取平均值,能够突出显示信号中的显著变化部分。
通过滑动窗口计算后的信号平均值,可以观察到信号中的异常部分。这些异常部分可能是由于嵌入了flag信息所导致的。
绘制滑动平均后的信号图,从图中手动确定异常信号段的起始位置为5000。
- 提取异常信号段:
根据观察到的起始位置提取异常信号段。先取一个足够长的段-作为示例进行分析。
提取信号段后,可以进一步处理和分析该信号段,以便恢复其中的嵌入信息。
- 尝试通过格基恢复原始的秘密向量:
从信号中提取格基信息并进行校验。提取插入的信号段,恢复出整数向量。
- 绘制信号图以供观察:
将插入flag信息后的信号可视化,展示其结构和插入位置。
import numpy as np
import matplotlib.pyplot as plt
signal_with_lattice = np.load('simple_test_lattice_signal.npy')
start_index = 5000
extracted_signal = signal_with_lattice[start_index:start_index + n]
print("Extracted Signal:", extracted_signal)
simple_basis = np.eye(n)
print("Simple Basis:\n", simple_basis)
recovered_vector = np.round(extracted_signal).astype(int)
print("Recovered Vector:", recovered_vector)
recovered_flag = ''.join([chr(coord) for coord in recovered_vector])
print("Recovered Flag:", recovered_flag)
if recovered_flag == flag:
print("Flag successfully recovered!")
else:
print("Failed to recover the flag correctly.")
window_size = 100
signal_mean = np.convolve(np.abs(signal_with_lattice), np.ones(window_size) / window_size, mode='valid')
plt.figure(figsize=(15, 5))
plt.plot(signal_mean, label='Mean Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Sliding Window Mean of Signal')
plt.legend()
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()
plt.figure(figsize=(15, 5))
plt.plot(extracted_signal, label='Extracted Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Extracted Signal for Analysis')
plt.legend()
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()
plt.figure(figsize=(10, 10))
plt.imshow(simple_basis, cmap='viridis')
plt.colorbar()
plt.title('Simple Basis Matrix')
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()
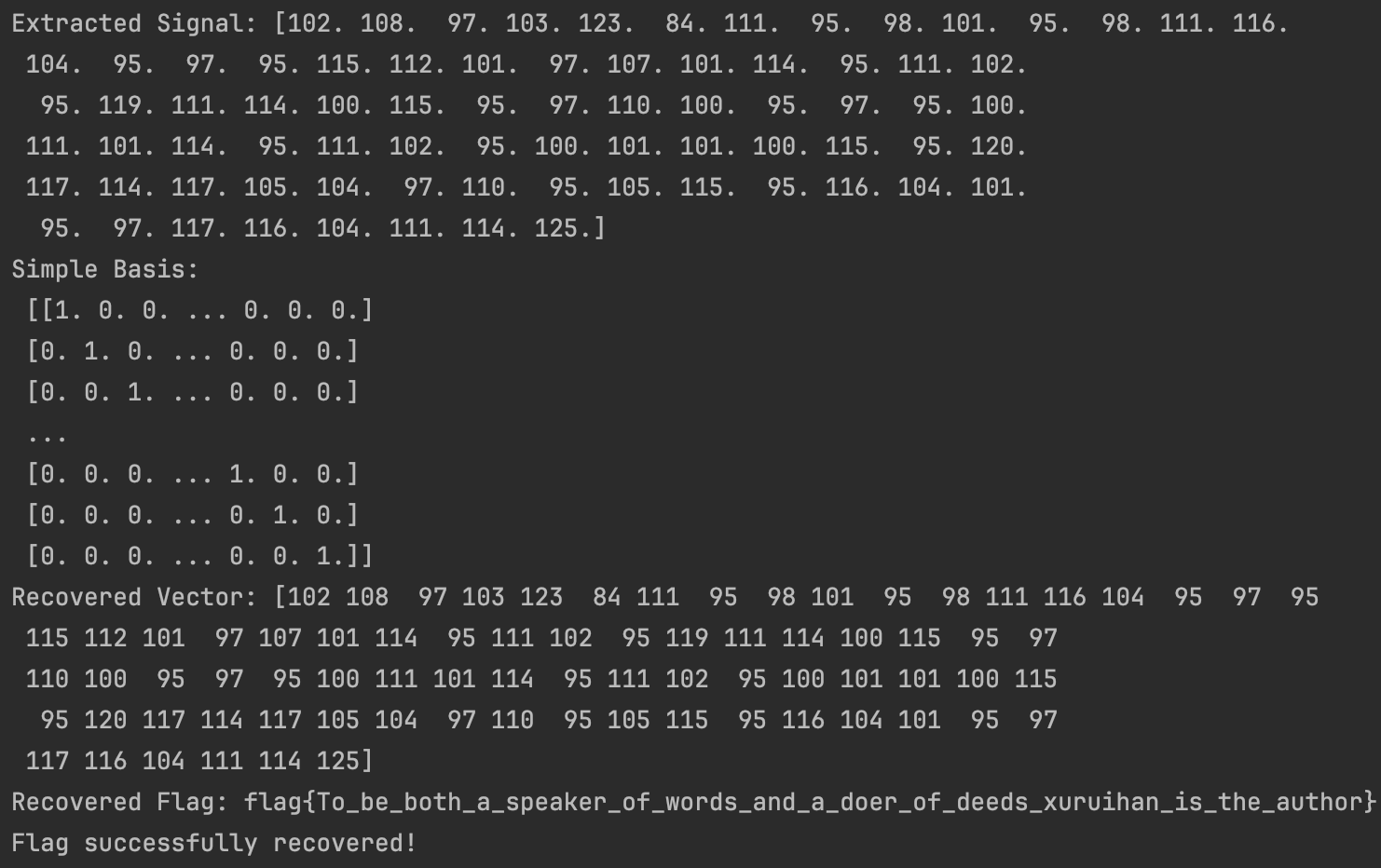
代码运行成功后可获得flag:Extracted Signal: [102. 108. 97. 103. 123. 84. 111. 95. 98. 101. 95. 98. 111. 116.
104. 95. 97. 95. 115. 112. 101. 97. 107. 101. 114. 95. 111. 102.
95. 119. 111. 114. 100. 115. 95. 97. 110. 100. 95. 97. 95. 100.
111. 101. 114. 95. 111. 102. 95. 100. 101. 101. 100. 115. 95. 120.
117. 114. 117. 105. 104. 97. 110. 95. 105. 115. 95. 116. 104. 101.
95. 97. 117. 116. 104. 111. 114. 125.]
Simple Basis:
[[1. 0. 0. ... 0. 0. 0.]
[0. 1. 0. ... 0. 0. 0.]
[0. 0. 1. ... 0. 0. 0.]
...
[0. 0. 0. ... 1. 0. 0.]
[0. 0. 0. ... 0. 1. 0.]
[0. 0. 0. ... 0. 0. 1.]]
Recovered Vector: [102 108 97 103 123 84 111 95 98 101 95 98 111 116 104 95 97 95
115 112 101 97 107 101 114 95 111 102 95 119 111 114 100 115 95 97
110 100 95 97 95 100 111 101 114 95 111 102 95 100 101 101 100 115
95 120 117 114 117 105 104 97 110 95 105 115 95 116 104 101 95 97
117 116 104 111 114 125]
Recovered Flag: flag{To_be_both_a_speaker_of_words_and_a_doer_of_deeds_xuruihan_is_the_author}
Flag successfully recovered!


4.2.3.代码分析
代码分析第一二步和4.1.3的一致,不再重复叙述,下同。若有不一样的地方会说明。
- 确定异常信号段起始位置:
start_index = 5000
n = len("flag{To_be_both_a_speaker_of_words_and_a_doer_of_deeds_xuruihan_is_the_author}")
extracted_signal = signal_with_lattice[start_index:start_index + n]
确定异常信号段的起始位置。
确定flag的长度,并提取相应长度的信号段。
- 打印提取的格点信号段:
print("Extracted Signal:", extracted_signal)
打印从信号中提取出的格点信号段。
- 定义简单的格基矩阵:
simple_basis = np.eye(n)
print("Simple Basis:\n", simple_basis)
使用单位矩阵作为简单的格基矩阵。
- 尝试通过格基恢复原始的秘密向量:
recovered_vector = np.round(extracted_signal).astype(int)
print("Recovered Vector:", recovered_vector)
通过格基矩阵恢复信号中的秘密向量。打印恢复的秘密向量。
- 恢复flag信息:
recovered_flag = ''.join([chr(coord) for coord in recovered_vector])
print("Recovered Flag:", recovered_flag)
将恢复的整数向量转换回字符,形成原始flag信息。打印恢复的flag信息。
- 校验结果:
if recovered_flag == flag:
print("Flag successfully recovered!")
else:
print("Failed to recover the flag correctly.")
校验恢复的flag信息是否正确。
- 分析信号,找到插入的格点信号段:
window_size = 100
signal_mean = np.convolve(np.abs(signal_with_lattice), np.ones(window_size) / window_size, mode='valid')
使用滑动窗口计算信号的平均值,以检测信号中的异常部分。
- 绘制滑动窗口均值图:
plt.figure(figsize=(15, 5))
plt.plot(signal_mean, label='Mean Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Sliding Window Mean of Signal')
plt.legend()
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()
绘制信号的滑动窗口均值图,添加横纵坐标的虚线。
- 绘制提取的信号段:
plt.figure(figsize=(15, 5))
plt.plot(extracted_signal, label='Extracted Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Extracted Signal for Analysis')
plt.legend()
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()
绘制提取的信号段,添加横纵坐标的虚线。
- 绘制简单的格基矩阵图:
plt.figure(figsize=(10, 10))
plt.imshow(simple_basis, cmap='viridis')
plt.colorbar()
plt.title('Simple Basis Matrix')
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.show()
绘制简单的格基矩阵图,添加横纵坐标的虚线。
4.3.complex_lattice_signal
4.3.1.出题思路
这个题和上一个思路差不多,只是把单位格基改成了随机格基,题目是有四个文件,随机格数据,flag数据文件和随机格基图以及频谱图




- 基础知识考察:
通过定义和转换flag信息,考察对字符串编码和二进制处理的理解。
生成随机格基矩阵,考察对线性代数中矩阵和向量运算的理解。
- 信号处理:
通过生成随机信号并插入信息,考察对信号生成和处理的能力。
通过滑动窗口检测异常信号段,考察信号异常检测的应用。
- 数据提取与校验:
提取并校验嵌入信号中的信息,考察对信号提取和数据校验的综合应用能力。
- 可视化:
通过绘制矩阵和信号图,考察数据可视化能力
4.3.2.解题思路
解题思路和4.2.2一致。

代码运行成功后即可获得flag
Extracted Signal: [ -3241. 7365. 8663. -996. 459. -2790. -453. 819. -4828.
-8637. -14295. -7889. 1858. 621. -587. 2861. -9836. -1517.
-1811. -852. 1730. -3511. -14536. 6126. -5694. -9660. -5961.
1153. -15094. -3193. -5850. -7103. -2635. -4810. -3182. 2933.
-6391. 2698. -4060. 3014. 382. -10535. -4254. 4612. 2426.
-1673. -13083. -8207. -7799. -1622. 5125. -12946. 2165. 1328.
-11978. -3926. 3637. -6808. -1950. -3479. -7730. -8254. -8930.
-5098. -14334. -2853. -10597. 4689. -5133. -2171. 6364. -8551.
1531. 659. -9558. -6221. -4700. -8681.]
Random Basis:
[[ -4 9 4 ... -10 -4 -2]
[-10 1 -3 ... -10 8 -1]
[ 1 4 -2 ... 5 5 -8]
...
[ 6 9 7 ... 6 -6 1]
[ -5 -2 9 ... -2 2 -3]
[ 3 -10 6 ... 9 5 -4]]
Recovered Flag: flag{To_be_both_a_speaker_of_words_and_a_doer_of_deeds_xuruihan_is_the_author}
Flag successfully recovered!


4.3.3.代码分析
加载文件和频谱图展示部分分析与4.1.3、4.2.3一致,所以只对关键代码进行分析。
- 确定信号段长度,通过读取随机基矩阵的维度来确定
random_basis = np.load('random_basis.npy')
n = random_basis.shape[0]
加载保存的随机基矩阵,并确定其维度。信号段的长度与基矩阵的维度相同。
- 提取异常信号段
extracted_signal = signal_with_lattice[start_index:start_index + n]
从信号中提取出长度为n的异常信号段。
- 通过格基恢复原始的秘密向量
recovered_vector = np.round(np.dot(extracted_signal, np.linalg.inv(random_basis))).astype(int)
recovered_flag = ''.join([chr(coord) for coord in recovered_vector])
print("Recovered Flag:", recovered_flag)
使用随机基矩阵的逆矩阵将提取的信号段转换回原始的秘密向量,并将其转为字符串形式的flag信息。
打印恢复的flag信息。
4.4.chacha20_complex_lattice_signal
这道题和上一个类似,不同之处在于加了chacha20加密了噪声,你需要通过降噪并恢复flag。为了保证题目能解出,加的噪声参数很小,只是一个小磕绊的弯弯绕绕。题目利用了ChaCha20流密码算法与格基理论,结合模拟电磁信号数据,设计了一道涉及密码学和信号处理的复杂解密题目
首先介绍一下chacha20,ChaCha20 是由丹尼尔·J·伯恩斯坦(Daniel J. Bernstein)设计的一种流加密算法。它以其简单高效的软件实现而著称,它通过对称密钥加密数据流ChaCha20 使用 256 位的密钥和 96 位的随机数(nonce),对 64 字节的块进行 20 轮变换来确保安全性。
- 基本概念
ChaCha20 的核心是 512 位的状态矩阵,该矩阵由 16 个 32 位的字组成,具体包括:
- 4 个常量(固定不变)
- 8 个密钥字(256 位密钥)
- 1 个 64 位的计数器(表示当前处理的数据块序号)
- 3 个 32 位的随机数(Nonce)
状态矩阵的初始形式如下:
State = [ C0, C1, C2, C3, K0, K1, K2, K3, K4, K5, K6, K7, Ctr, N0, N1, N2 ]
其中:
-
C0, C1, C2, C3 是常量,通常为 “expand 32-byte k” 的 ASCII 编码。
-
K0 到 K7 是密钥。
-
Ctr 是块计数器。
-
N0 到 N2 是随机数(Nonce)。
-
四分之一轮操作(Quarter Round)
四分之一轮操作是 ChaCha20 的核心运算,作用于状态矩阵的 4 个字。其数学表达如下:
对于四个 32 位字 (a, b, c, d) 进行以下操作:
a += b; d ^= a; d = ROTL(d, 16)
c += d; b ^= c; b = ROTL(b, 12)
a += b; d ^= a; d = ROTL(d, 8)
c += d; b ^= c; b = ROTL(b, 7)
其中,ROTL(x, n) 表示将 x 左循环移位 n 位。
- ChaCha20 轮函数
ChaCha20 轮函数由 20 轮操作组成,每轮包括 8 个四分之一轮操作。每轮包括两种模式:
奇数轮操作在列上进行。
偶数轮操作在对角线上进行。
具体步骤如下:
- 列操作:
对每一列(从左到右)执行四分之一轮操作。
- 对角线操作:
对每个对角线(从左上到右下和从左下到右上)执行四分之一轮操作。
经过 20 轮操作后,将当前状态矩阵与初始状态矩阵逐字相加,生成 512 位的密钥流块。
加密和解密过程
ChaCha20 的加密和解密过程通过将密钥流块与明文/密文进行逐字节异或实现:
密文 = 明文 ⊕ 密钥流块
明文 = 密文 ⊕ 密钥流块
- 数学特性和安全性
线性复杂性:每个四分之一轮操作包括加法、异或和循环移位,均为线性复杂度操作。
扩散性:每轮操作后,状态矩阵中的每个字都被更新,确保每一比特的变化会影响到整个矩阵,增加密文的扩散性和安全性。
抗分析性:ChaCha20 经过多轮变换和复杂的非线性操作,增加了其抗密码分析的能力。
4.4.1.出题思路
题目是有四个文件,格数据,flag数据文件和随机格基图以及频谱图




- 定义和编码Flag信息
首先,将待解密的flag信息定义并转换为二进制表示形式,然后进一步转化为整数向量。这一步的目的是为了将flag信息以整型向量的形式参与后续的加密和嵌入过程。
- 生成随机格基矩阵
使用numpy生成一个随机的格基矩阵,并确保其行向量线性无关(即行满秩)。然后通过该矩阵生成一个格点,将其与秘密向量相乘得到格点信息。这个过程是为了将秘密向量嵌入到一个高维的格点中,以增加解密的难度。
- 生成并加密电磁信号数据
生成一个模拟的电磁信号数据,并使用ChaCha20流密码算法对噪声进行加密。通过对噪声数据进行加密,使得信号数据具有更高的复杂性和安全性。
- 将格点信号嵌入电磁信号中
在正常信号的特定位置嵌入格点信息,并保存生成的数据文件。这一步是为了在实际的电磁信号中嵌入加密的秘密信息,模拟真实的电磁环境中的数据传输。
- 绘制信号图
通过绘制信号图,直观展示嵌入格点后的信号变化。通过图像展示,可以更直观地理解加密和嵌入过程中的信号变化情况。
- 重点
ChaCha20 加密算法:利用ChaCha20流密码算法对噪声数据进行加密,增加信号的复杂性和安全性。
格基理论:使用随机格基矩阵将秘密向量转换为高维格点,并嵌入到电磁信号中。
信号处理:模拟真实的电磁信号环境,生成复杂的电磁信号数据,并在其中嵌入加密的格点信息。
通过这些步骤,题目不仅考察ChaCha20加密算法的理解,还结合了线性代数和信号处理的知识,增加了解题的难度。
4.4.2.解题思路
重复的就不说了,直接说重点
- 读取随机基矩阵:
使用np.load函数读取保存的随机基矩阵文件,并确定基矩阵的维度n。
- 提取信号段并恢复秘密向量:
使用信号段和随机基矩阵的逆矩阵,计算并恢复秘密向量。
- 恢复flag信息:
将恢复的向量转换为字符,拼接成flag信息。
- ChaCha20解密噪声:
使用预先设定的密钥和nonce初始化ChaCha20解密器,解密噪声信号。
import numpy as np
import matplotlib.pyplot as plt
from Crypto.Cipher import ChaCha20
# 读取信号数据
signal_with_lattice = np.load('chacha20_complex_test_lattice_signal.npy')
# 假设手动确定了异常信号段起始位置
start_index = 5000
# 读取随机基矩阵
random_basis = np.load('chacha20_random_basis.npy')
n = random_basis.shape[0]
# 提取信号段并恢复秘密向量
extracted_signal = signal_with_lattice[start_index:start_index + n]
print("Extracted Signal:", extracted_signal)
# 使用随机格基的逆矩阵来恢复秘密向量
recovered_vector = np.round(np.dot(extracted_signal, np.linalg.inv(random_basis)) / 10).astype(int) # 恢复时需要除以增强倍数
print("Recovered Vector:", recovered_vector)
# 恢复的flag信息
recovered_flag = ''.join([chr(coord) for coord in recovered_vector])
print("Recovered Flag:", recovered_flag)
# 校验结果
if "flag{" in recovered_flag and "}" in recovered_flag:
print("Flag successfully recovered!")
else:
print("Failed to recover the flag correctly.")
# ChaCha20解密噪声
key = b'Sixteen byte key'
nonce = b'Unique nonce'
cipher = ChaCha20.new(key=key, nonce=nonce)
# 提取加密噪声段
encrypted_noise_signal = signal_with_lattice[:start_index]
noise = cipher.decrypt(encrypted_noise_signal.astype(np.uint8).tobytes())
recovered_noise = np.frombuffer(noise, dtype=np.uint8).astype(np.float32)
recovered_noise -= 128
# 校验解密的噪声
plt.figure(figsize=(15, 5))
plt.plot(recovered_noise, label='Recovered Noise Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Recovered Noise Signal using ChaCha20 Decryption')
plt.legend()
plt.grid(True)
plt.show()
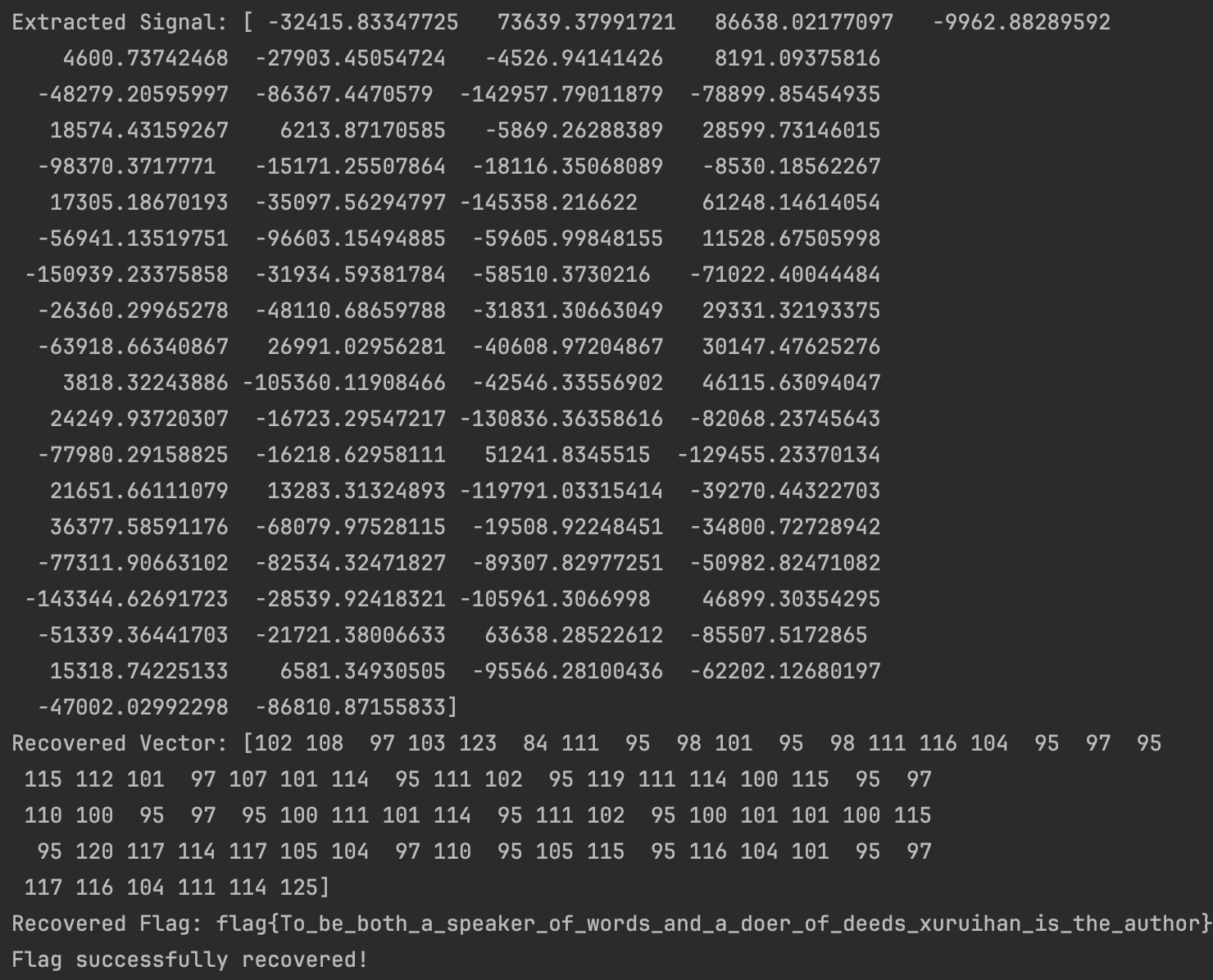
代码运行成功即可获取flagExtracted Signal: [ -32415.83347725 73639.37991721 86638.02177097 -9962.88289592
4600.73742468 -27903.45054724 -4526.94141426 8191.09375816
-48279.20595997 -86367.4470579 -142957.79011879 -78899.85454935
18574.43159267 6213.87170585 -5869.26288389 28599.73146015
-98370.3717771 -15171.25507864 -18116.35068089 -8530.18562267
17305.18670193 -35097.56294797 -145358.216622 61248.14614054
-56941.13519751 -96603.15494885 -59605.99848155 11528.67505998
-150939.23375858 -31934.59381784 -58510.3730216 -71022.40044484
-26360.29965278 -48110.68659788 -31831.30663049 29331.32193375
-63918.66340867 26991.02956281 -40608.97204867 30147.47625276
3818.32243886 -105360.11908466 -42546.33556902 46115.63094047
24249.93720307 -16723.29547217 -130836.36358616 -82068.23745643
-77980.29158825 -16218.62958111 51241.8345515 -129455.23370134
21651.66111079 13283.31324893 -119791.03315414 -39270.44322703
36377.58591176 -68079.97528115 -19508.92248451 -34800.72728942
-77311.90663102 -82534.32471827 -89307.82977251 -50982.82471082
-143344.62691723 -28539.92418321 -105961.3066998 46899.30354295
-51339.36441703 -21721.38006633 63638.28522612 -85507.5172865
15318.74225133 6581.34930505 -95566.28100436 -62202.12680197
-47002.02992298 -86810.87155833]
Recovered Vector: [102 108 97 103 123 84 111 95 98 101 95 98 111 116 104 95 97 95
115 112 101 97 107 101 114 95 111 102 95 119 111 114 100 115 95 97
110 100 95 97 95 100 111 101 114 95 111 102 95 100 101 101 100 115
95 120 117 114 117 105 104 97 110 95 105 115 95 116 104 101 95 97
117 116 104 111 114 125]
Recovered Flag: flag{To_be_both_a_speaker_of_words_and_a_doer_of_deeds_xuruihan_is_the_author}
Flag successfully recovered!
频谱图和4.4.3的解释一样,不再重复解释。
4.5lwe
这道题参考了2024Crypto的顶会论文,全称“Crypto Conference”,是密码学领域最重要的国际会议之一。Crypto Conference由国际密码学研究协会(IACR)组织,是每年举办的三大顶级密码学会议之一,另外两个分别是欧洲密码学会议(Eurocrypt)和亚洲密码学会议(Asiacrypt)Crypto Conference自1981年开始举办,至今已有40多年的历史。会议通常在每年的八月下旬至九月初于美国加州圣巴巴拉的加州大学圣巴巴拉分校(UCSB)举行。
@inproceedings{crypto-2024-34347,
title={Adaptively Sound Zero Knowledge SNARKs for UP},
publisher={Springer-Verlag},
author={Surya Mathialagan and Spencer Peters and Vinod Vaikuntanathan},
year=2024
}
因文章篇幅原因,在此仅对题目所涉及的内容进行简单介绍,论文详情我附在了引用里,感兴趣的可以下载论文进行学习。
这篇论文的主要内容是研究UP类问题的自适应安全零知识SNARK(succinct non-interactive arguments of knowledge)。UP(Unambiguous Polynomial time)是NP问题的一个子类,其中每个实例最多只有一个见证。
-
从次指数级的学习错误(subexponential Learning With Errors,LWE)和一种新的LWE变种(evasive LWE)构建出一种可重复使用且自适应安全的零知识指定验证者SNARG(dvSNARG),其证明长度为 ( 1 + o ( 1 ) ) ⋅ λ (1 + o(1)) · λ (1+o(1))⋅λ比特,声音错误率为 2 − λ 2^-λ 2−λ。
-
提出了一种通用的转换方法,可以将任何“Sahai-Waters-like”的zk-SNARG提升为在指定验证者设置下的自适应安全zk-SNARG。
-
提出了一种通用转换方法,将任何自适应安全的zk-SNARG for UP提升为自适应安全的zk-SNARK for UP,同时保持零知识属性。
学习错误(LWE)假设
LWE假设:给定参数 $n, m, q \in \mathbb{N}
和
和
和\sigma, \delta > 0$,次指数级LWE假设
L
W
E
δ
n
,
m
,
q
,
σ
LWE_\delta^{n,m,q,\sigma}
LWEδn,m,q,σ
(
A
,
s
A
+
e
)
≈
c
(
A
,
b
)
(A, sA + e) \approx_c (A, b)
(A,sA+e)≈c(A,b)
其中,
s
←
U
(
Z
q
n
)
,
A
←
U
m
a
t
h
b
b
Z
q
n
×
m
,
e
←
D
Z
,
σ
m
,
b
←
Z
q
m
s\leftarrow U(\mathbb{Z}_q^n), A \leftarrow Umathbb{Z}_q^{n \times m}, e \leftarrow D_\mathbb{Z,\sigma}^m, b \leftarrow \mathbb{Z}_q^m
s←U(Zqn),A←UmathbbZqn×m,e←DZ,σm,b←Zqm
Puncturable PRF(可戳伪随机函数)
- 定义:一个可戳伪随机函数族在密钥空间
K
=
{
K
λ
}
λ
K = \{K_\lambda\}_\lambda
K={Kλ}λ、域
X
=
{
X
λ
}
λ
X = \{X_\lambda\}_\lambda
X={Xλ}λ、输出空间
Y
=
{
Y
λ
}
λ
Y = \{Y_\lambda\}_λ
Y={Yλ}λ 和多项式
s
(
λ
)
s(\lambda)
s(λ)上是一个包含以下算法的PPT算法组:
- P P R F . G e n ( 1 λ ) PPRF.Gen(1^\lambda) PPRF.Gen(1λ):生成密钥 k ∈ K λ k \in K_\lambda k∈Kλ。
- P P R F . P u n c ( k , S ) PPRF.Punc(k, S) PPRF.Punc(k,S):输入密钥 k ∈ K λ k \in K_\lambda k∈Kλ 和集合 S ⊆ X λ S \subseteq X_\lambda S⊆Xλ,输出新的密钥 k { S } ∈ K λ k^{\{S\}} \in K_\lambda k{S}∈Kλ。
- P P R F . E v a l ( k , x ) PPRF.Eval(k, x) PPRF.Eval(k,x):输入密钥 k ∈ K λ k \in K_\lambda k∈Kλ 和 x ∈ K λ x \in K_\lambda x∈Kλ,输出值 y ∈ Y λ y \in Y_\lambda y∈Yλ。
混淆(Obfuscation)
- σ-matrix PRFs:一种使用矩阵分支程序计算的带有噪声的伪随机函数族,满足特定的平均情况下的混淆属性。具体的混淆方案基于evasive LWE构建,具有以下形式:
- 矩阵编码(GGH编码):使用随机矩阵 A ∈ Z q ( n + w ) × 4 ( n + w ) log q A \in \mathbb{Z}_q^{(n+w) \times 4(n+w) \log q} A∈Zq(n+w)×4(n+w)logq和噪声矩阵 E E E进行编码。
- 安全性证明依赖于LWE和evasive LWE假设,使用逐步混淆的方法来逐层移除矩阵,同时保持伪随机性。
证明构造
- SNARK证明:基于自适应安全的SNARG,通过引入全同态加密(FHE)和公钥加密(PKE)来构建SNARK。
- 生成过程包括生成全同态加密密钥对和公钥加密密钥对,并使用这些密钥对将关系转换为新的UP关系。
- 证明者使用全同态加密和公钥加密生成证明,而验证者使用原始SNARG系统验证。
这篇论文通过详细的理论推导和构造,展示了如何在次指数级可证伪假设下构建自适应安全的零知识SNARK,从而推进了SNARK在密码学中的应用。
4.5.2.出题思路
题目有3个文件,包含flag信息的数据文件,题目有3个文件,包含flag信息的数据文件,格基矩阵文件,显示嵌入flag信息的格基信息图。



这道题目通过处理和分析嵌入有特定标志信息的LWE样本信号数据,考察对信号处理、统计特征分析以及LWE理论的理解和应用。
- 加载和显示信号数据
提供包含嵌入flag信息的LWE信号数据文件和对应的格基矩阵文件。
要求使用数据可视化工具对信号数据和格基矩阵进行可视化展示,以便直观地观察和理解数据特征。
- 信号数据降噪
提供一个常见的信号处理技术(如Savitzky-Golay滤波器)。
要求对原始信号数据进行降噪处理,并展示处理后的信号数据,以观察降噪效果。
- 分析信号数据的统计特征
通过分析信号数据的统计特征,推导出LWE问题的相关参数(如安全参数 n n n、模数 q q q、噪声参数 σ σ σ)计算信号数据的长度、最大值、标准差等统计特征。
根据这些统计特征估计LWE问题中的相关参数,例如,利用信号数据的最大值估计模数 q q q,利用标准差估计噪声参数 σ σ σ。
- 解码嵌入的flag信息
通过LWE理论对信号数据进行解码,提取嵌入的信息(flag),主要对LWE解码过程的理解和实现能力。
4.5.3.解题思路
学习错误(LWE)假设
学习错误(LWE)假设是基于格的加密算法的基础,其基本形式可以表示为:
A
⋅
s
+
e
≡
b
(
m
o
d
q
)
A \cdot s + e \equiv b \pmod{q}
A⋅s+e≡b(modq)
其中:
- A A A 是一个随机生成的矩阵。
- s s s是秘密向量。
- e e e是误差向量,其元素通常从某个离散高斯分布中采样。
- q q q是一个模数。
信号数据处理和参数估计
- 模数 q q q的估计:
q = 2 ⌈ log 2 ( max_value ) ⌉ q = 2^{\lceil \log_2(\text{max\_value}) \rceil} q=2⌈log2(max_value)⌉
其中,max_value是信号数据的最大绝对值。
- 噪声参数 σ \sigma σ的估计:
σ = std(signals) 3 \sigma = \frac{\text{std(signals)}}{3} σ=3std(signals)
其中,std(signals) 是信号数据的标准差。
- 信号数据降噪
使用Savitzky-Golay滤波器对信号数据进行降噪处理,公式如下:
Savitzky-Golay滤波器:
d e n o i s e d s i g n a l s = s a v g o l f i l t e r ( b w i t h f l a g , 101 , 3 ) denoised_signals = savgol_filter(b_with_flag, 101, 3) denoisedsignals=savgolfilter(bwithflag,101,3)
其中,窗口大小为101,多项式阶数为3。
统计特征分析和参数估计
代码中分析信号数据的统计特征,并估计LWE参数:
- 模数 q q q的估计:
q = 2 ⌈ log 2 ( max_value ) ⌉ q = 2^{\lceil \log_2(\text{max\_value}) \rceil} q=2⌈log2(max_value)⌉
- 噪声参数 σ \sigma σ的估计:
σ = np.std(signals) 3 \sigma = \frac{\text{np.std(signals)}}{3} σ=3np.std(signals)
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import savgol_filter
def extract_flag_from_lwe_sample(signals, q, n):
binary_str = ''.join([str(val & 1) for val in signals])
patterns = ["01100110011011000110000101100111"]
for pattern in patterns:
flag_start_index = binary_str.find(pattern)
if flag_start_index != -1:
break
else:
return "Flag not found"
flag_length_bits = len(''.join(format(ord(char), '08b') for char in "flag{To_be_both_a_speaker_of_words_and_a_doer_of_deeds_xuruihan_is_the_author}"))
flag_binary_str = binary_str[flag_start_index:flag_start_index + flag_length_bits]
flag_chars = [chr(int(flag_binary_str[i:i+8], 2)) for i in range(0, flag_length_bits, 8)]
return ''.join(flag_chars)
b_with_flag = np.load('lwe_with_flag.npy')
A = np.load('lwe_with_flag_A.npy')
extracted_flag = extract_flag_from_lwe_sample(b_with_flag, q, n)
print(f"Extracted Flag: {extracted_flag}")
plt.figure(figsize=(10, 6))
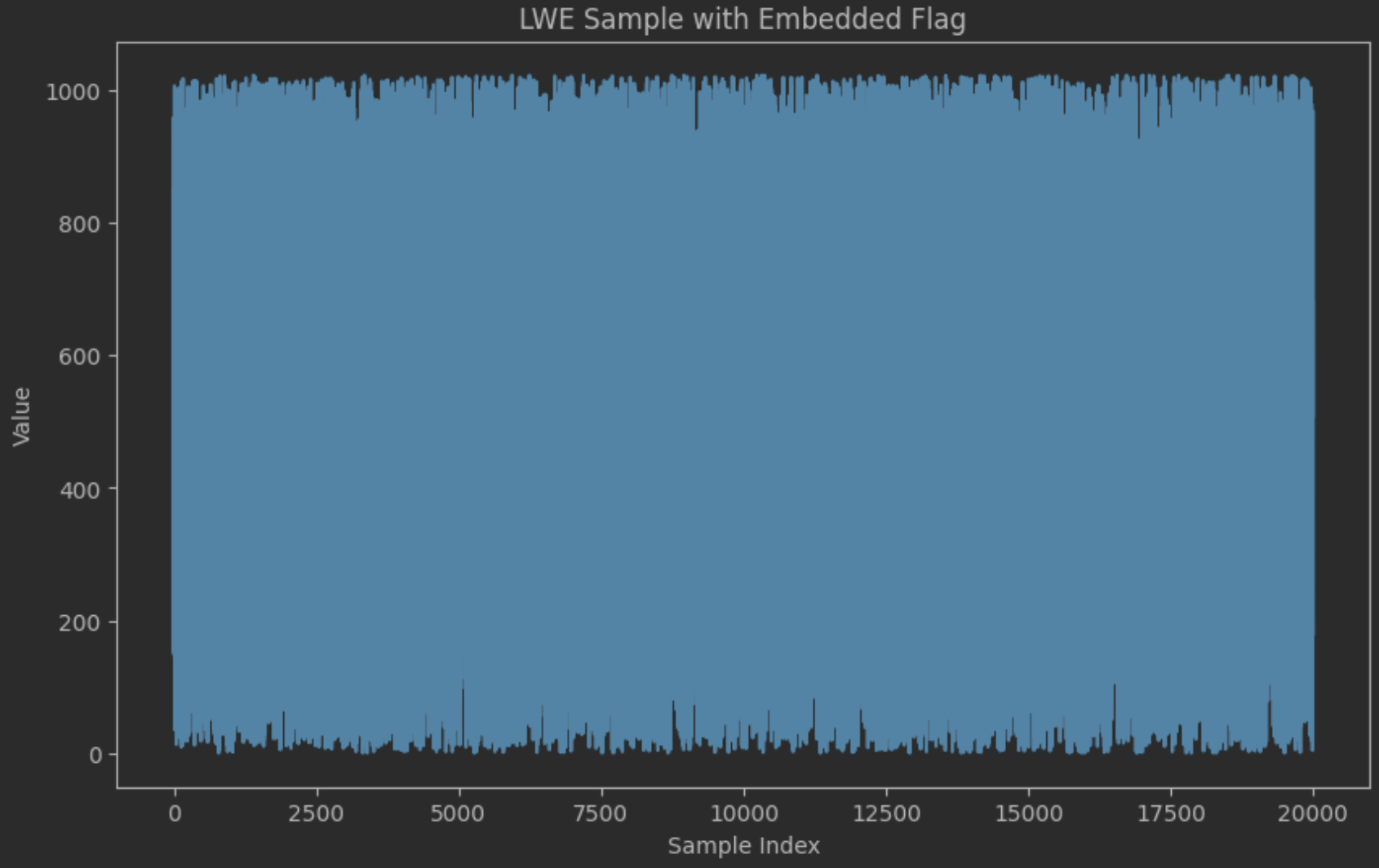
plt.plot(b_with_flag)
plt.title('LWE Sample with Embedded Flag')
plt.xlabel('Sample Index')
plt.ylabel('Value')
plt.show()
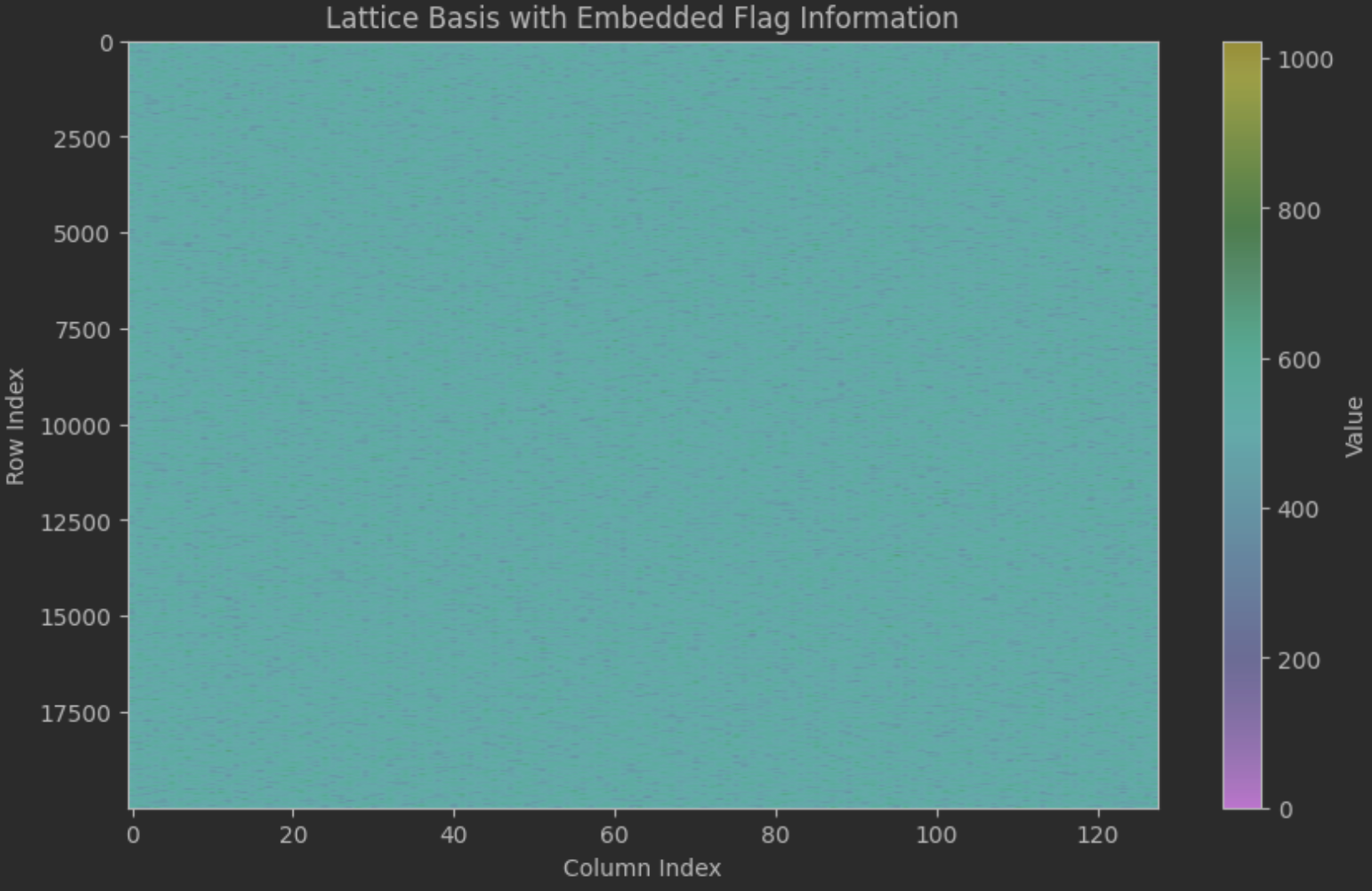
plt.figure(figsize=(10, 6))
plt.imshow(A, cmap='viridis', aspect='auto')
plt.title('Lattice Basis with Embedded Flag Information')
plt.xlabel('Column Index')
plt.ylabel('Row Index')
plt.colorbar(label='Value')
plt.show()
denoised_signals = savgol_filter(b_with_flag, 101, 3) # window size 101, polynomial order 3
plt.figure(figsize=(10, 6))
plt.plot(denoised_signals)
plt.title('Denoised LWE Sample with Embedded Flag')
plt.xlabel('Sample Index')
plt.ylabel('Value')
plt.show()
def estimate_lwe_parameters(signals, lattice_basis):
signal_length = len(signals)
n = 1 if signal_length < 1024 else 64
max_value = np.max(np.abs(signals))
q = int(2**np.ceil(np.log2(max_value)))
sigma = np.std(signals) / 3
return n, q, sigma
n, q, sigma = estimate_lwe_parameters(denoised_signals, A)
print(f"Estimated LWE Parameters: n={n}, q={q}, sigma={sigma}")

Estimated LWE Parameters: n=64, q=1024, sigma=98.47414168241636
Extracted Flag: flag{To_be_both_a_speaker_of_words_and_a_doer_of_deeds_xuruihan_is_the_author}

4.5.3.代码分析
篇幅限制,只对关键代码进行分析,加载数据文件和频谱图代码已在上述相关环节进行过解释,不再进行详细说明。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import savgol_filter
导入必要的库:numpy用于处理数组,matplotlib.pyplot用于绘图,scipy.signal.savgol_filter用于信号降噪。
def extract_flag_from_lwe_sample(signals, q, n):
binary_str = ''.join([str(val & 1) for val in signals])
patterns = ["01100110011011000110000101100111"]
for pattern in patterns:
flag_start_index = binary_str.find(pattern)
if flag_start_index != -1:
break
else:
return "Flag not found", -1
flag_length_bits = len(''.join(format(ord(char), '08b') for char in "flag{To_be_both_a_speaker_of_words_and_a_doer_of_deeds_xuruihan_is_the_author}"))
flag_binary_str = binary_str[flag_start_index:flag_start_index + flag_length_bits]
flag_chars = [chr(int(flag_binary_str[i:i+8], 2)) for i in range(0, flag_length_bits, 8)]
return ''.join(flag_chars), flag_start_index, flag_length_bits
定义了一个函数extract_flag_from_lwe_sample,用于从信号数据中提取嵌入的flag信息。首先,将信号数据转换为二进制字符串,然后查找特定的二进制模式('flag’的二进制表示)。找到模式后,提取对应长度的二进制字符串并转换为字符,返回提取的flag信息、起始索引和长度。
b_with_flag = np.load('lwe_with_flag.npy')
A = np.load('lwe_with_flag_A.npy')
加载LWE样本信号数据b_with_flag和对应的格基矩阵A。
def estimate_lwe_parameters(signals, lattice_basis):
signal_length = len(signals)
n = 1 if signal_length < 1024 else 64
max_value = np.max(np.abs(signals))
q = int(2**np.ceil(np.log2(max_value)))
sigma = np.std(signals) / 3
return n, q, sigma
定义了一个函数estimate_lwe_parameters,用于估计LWE参数。计算信号数据的长度、最大值、模数q和噪声参数sigma,并根据信号长度估计安全参数n。
n, q, sigma = estimate_lwe_parameters(b_with_flag, A)
print(f"Estimated LWE Parameters: n={n}, q={q}, sigma={sigma}")
调用estimate_lwe_parameters函数估计LWE参数,并打印估计的参数值。
extracted_flag, flag_start_index, flag_length_bits = extract_flag_from_lwe_sample(b_with_flag, q, n)
print(f"Extracted Flag: {extracted_flag}")
调用extract_flag_from_lwe_sample函数从信号数据中提取flag信息,并打印提取的flag。
denoised_signals = savgol_filter(b_with_flag, 101, 3)
使用Savitzky-Golay滤波器对信号进行降噪处理。
plt.figure(figsize=(10, 6))
plt.plot(denoised_signals)
if flag_start_index != -1:
plt.axvline(x=flag_start_index, color='r', linestyle='--')
plt.axvline(x=flag_start_index + flag_length_bits, color='r', linestyle='--')
plt.title('Denoised LWE Sample with Embedded Flag (Flag Region Highlighted)')
else:
plt.title('Denoised LWE Sample with Embedded Flag')
plt.xlabel('Sample Index')
plt.ylabel('Value')
plt.show()
显示降噪后的频谱图,并在图中用红色虚线标记包含flag信息的区域。如果未找到flag信息,则只显示降噪后的频谱图标题。
5.总结
感谢您能看到这里,路漫漫兮其修远兮,愿上下而求索。因鄙人没有硬件相关设备,无法捕捉到真实的电磁信号,示波器电路板相关设备成本高昂。在这个出题指南手册里,针对电磁侧信道攻击的数据都是模拟数据,若有读者拥有这方面的实验室设备,可以多多交流。再次感谢读者能看到最后,希望我的指南可以赢得您的点赞在看爱心一键三连~
1.Timing Attacks on Implementations of
Die-Hellman, RSA, DSS, and Other Systems
https://paulkocher.com/doc/TimingAttacks.pdf
2.The ChaCha family of stream ciphers
https://cr.yp.to/chacha.html


























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








