（重点）可导、连续、可微+（浅谈）可积 的关系以及例题深化理解

                                                     <本章均为网上资源的总结>                                                          

简单描述可导连续可微可积关系https://www.bilibili.com/video/BV1g5411s71v?from=search&seid=17073069093693841166&spm_id_from=333.337.0.0

* 先看可导、连续、可微、可积关系

    在a到b的区间中，将其中区域的f（x）去掉，函数依旧有可积性，毕竟求的是它面积嘛，但是连续就不是了

注意：这四个都能推出极限存在

可导必连续证明https://www.bilibili.com/video/BV13J411e7Dv?from=search&seid=17073069093693841166&spm_id_from=333.337.0.0

可微可导充要条件判断（好像在18:00左右）https://www.bilibili.com/video/BV1GQ4y1r77i?from=search&seid=15826877773207064833&spm_id_from=333.337.0.0

1.定义

一.可导

 

导数存在不能趋于正负无穷

二.连续

三.可微（一元）

可微的定义有些抽象，我更喜欢用几何的描述去理解 

 误差：线性增量减去实际增量

这里可微本质就是以直代曲的过程

2.关系条件

一.可导必连续，连续不一定可导

 存在尖点类似这个符号  ^   不可导

 当X趋于Xo时由以上证明过程得可导必连续

ps：逆否命题  不连续一定不可导（某点处）

二.可微与可导为充要

 可微可导连续过程离不开△x趋于0  

可微可导的式子都可以相互反推出来

四个例题理解概念https://www.bilibili.com/video/BV1hu411f7bE?spm_id_from=333.1007.top_right_bar_window_history.content.click

3.例题深化理解（本节重点）

①

 

 如何下手？

有可导用不上

可以先往极限的角度思考

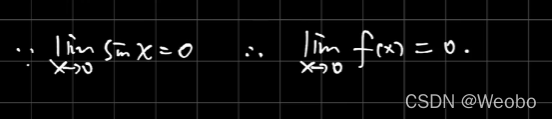在x趋于0时 分母趋于0，要想极限存在必定分子为0

 

 x=0可导那么必定能连续

直接可以得到f（0）=0，列出k的式子，因为x趋于0时，极限的等价无穷小替换，sinx~x，

就可列出导数的式子了，所以k=f’（0）=2

②

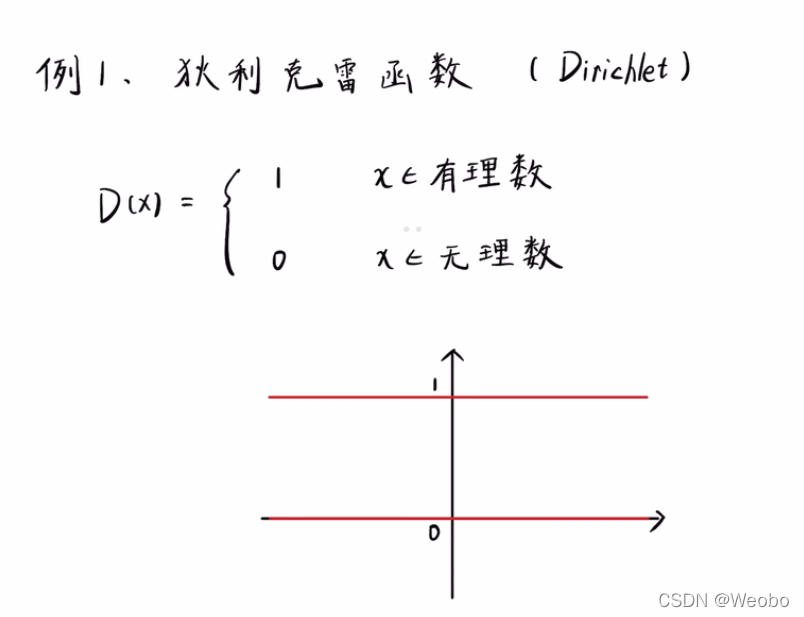
 表面看是连续的线，其实他们是由无数个点去点出来的，不连续，也不可导

③

 前面说过会有出现类似  ^  这个符号的尖点，到处都是这个尖点

它的效果图

 放大

 

 后期你再放大都会重复出现这个图像（在一个小区域都能出现无数个尖点）

④

 原因如下：

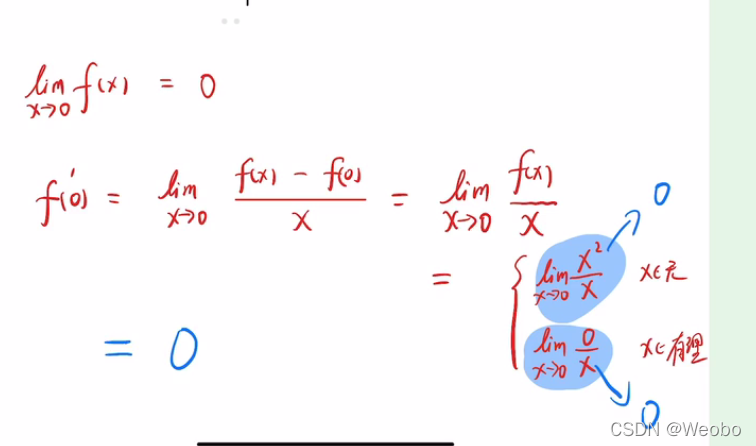
 乍看和②的例题很像，但是区别在0处是可导的，也只有这地方可导，其余皆否

⑤

解析如下：

 无穷小乘有界量，在x趋于0存在数值0，所以f（x）其他地方也是处处连续

 

如果直接列出导函数，你会发现f'(x)在X不等于0情况中X趋于0时有震荡点，则不连续 

但是为什么能列出所有导函数却在f’(x)却不连续呢？这不就不符合我们可导必连续的条件了吗？

 我们常常会直接把导数用求导法则直接求导，在X趋近Xo点时判定连续容易出错

原因是在单点求导时，f（x）可导与f’（x）连续并没有什么直接关系

 所以在判定某点连续时还需要用定义

这样就连续了，满足了可导必连续的条件