DSO初始化

1 点的提取及参数初始化

初始化开始先设置第一帧 CoarseInitializer::setFirst，主要步骤包括：
1）生成图像金字塔的内参 CoarseInitializer::makeK；
2）逐层提取一定数量的点（局部梯度大的点），在点的提取过程中通过划分网格来尽可能保证获得的点均匀分布在平面上，另外这里还考虑了点的梯度的均匀分布 PixelSelector::select；
3）初始化点的参数，其中逆深度初始化为1；
4）通过构建kdtree来找到每个点在像素平面上的相邻点 CoarseInitializer::makeNN。
接下来考虑如何根据后来帧的信息完成初始化 CoarseInitializer::trackFrame。

2 误差函数

设第一帧（参考帧）为$I_1$，第二帧（当前帧）为$I_2$，参考坐标系到当前坐标系的相对位姿为${\xi }_{21}\in \mathfrak{s}\mathfrak{e}(3)$， 假设参考帧中有一点${\mathbf{p}}_1$（像素坐标，这里及后续都是归一化坐标）被选中，当其深度（逆深度${\rho }_1$，初始化为1）和内参$\mathbf{K}$（通过事先标定获得）已知时，可以通过一次逆投影变换${\pi }^{-1}(\mathbf{x})$得到参考帧坐标系下的三维点坐标${\mathbf{P}}_1$:
$${\mathbf{P}}_1={\pi }^{-1}({\mathbf{p}}_1)={\mathbf{K}}^{-1}{\mathbf{p}}_1/{\rho }_1\text{\hspace{1em}(1)}$$
其对应于当前帧中的像素坐标${\mathbf{p}}_2$可以经过给定位姿变换后再通过一次投影变换获得：
$${\mathbf{p}}_2=\pi (\exp ({\xi }_{21}^{\wedge }){\mathbf{P}}_1)=\pi (\exp ({\xi }_{21}^{\wedge }){\pi }^{-1}({\mathbf{p}}_1))\text{\hspace{1em}(2)}$$
由于直接法严重依赖光照不变性假设，DSO在误差函数中加入了光度变换参数$[a,b{]}^T$来增强系统的可靠性，即理想情况下，所有追踪的点在前后两帧中满足：
$$I_2({\mathbf{p}}_2)=\exp (a)I_1({\mathbf{p}}_1)+b\text{\hspace{1em}(3)}$$
这里的$[a,b{]}^T$当然是相对值了，这里的$\exp (a)$等效于原文公式（4）中的$\frac{t_j\exp (a_j)}{t_i\exp (a_i)}$，因此当曝光时间$t_1,t_2$已知时，可以将其转化为对数形式，作为$a$的初值，即$a=\log (t_2/t_1)$，然后根据光照不变假设可以定义单个点的误差
$$r({\mathbf{p}}_1)=I_2({\mathbf{p}}_2)-\exp (a)I_1({\mathbf{p}}_1)-b\text{\hspace{1em}(4)}$$
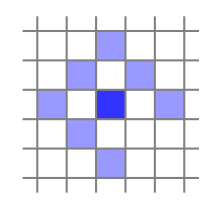
当然，单个点的区分度太小，因此DSO选取了一个包含8个点的小块，如图1所示

Fig. 1

对每个点的误差加权求和之后得到整体的残差能量函数(Huber范数形式)：
$$E_{\mathbf{p}}=\sum _{{\mathbf{p}}_1\in \mathcal{N}(\mathbf{p})}{w}_{\mathbf{p}}\Vert I_2({\mathbf{p}}_2)-\exp (a)I_1({\mathbf{p}}_1)-b{\Vert }_{\gamma }=\sum _{{\mathbf{p}}_1\in \mathcal{N}(\mathbf{p})}{w}_{\mathbf{p}}H(r({\mathbf{p}}_1))\text{\hspace{1em}(5)}$$
其中
$$w_{\mathbf{p}}=\frac{c^2}{c^2+\Vert \nabla I(\mathbf{p}){\Vert }_2^2}\text{\hspace{1em}(6)}$$
用来降低高梯度点的权重。
Huber范数可以写成如下形式：
$$H(r)=\{\begin{array}{ll}{r}^2/2& \text{,∣r∣<σ}\\ \sigma (|r|-\sigma /2)& \text{,∣r∣>=σ}\end{array}\text{\hspace{1em}(7)}$$
其中$\sigma$是一个常数，在DSO源码中被设为9。为了和代码一致，设
$$w_h=\{\begin{array}{ll}1& \text{,∣r∣<σ}\\ \sigma /|r|& \text{,∣r∣>=σ}\end{array}\text{\hspace{1em}(8)}$$
这样公式（7）就变成了
$$H(r)=w_h{r}^2(1-w_h/2)\text{\hspace{1em}(9)}$$
对参考帧中所有能投影到当前帧的点的误差进行累加，就得到了总的误差函数：
$$E=\sum E_{\mathbf{p}}\text{\hspace{1em}(10)}$$

3 高斯牛顿法

高斯牛顿法是求解非线性最小二乘问题的一种常见方法，在非线性误差函数无法通过直接求导得到极值时，通过将该非线性误差函数一阶泰勒展开，寻找最优的状态增量，使整个误差函数逐步下降直至收敛。由于使用了Huber核函数，根据公式（9），我们将误差函数定义为：
$$f(\mathbf{x})=\sqrt{w_h}r=\sqrt{w_h}(I_2({\mathbf{p}}_2)-\exp (a)I_1({\mathbf{p}}_1)-b)\text{\hspace{1em}(11)}$$
这里是为了凑出一个平方项的形式，因为高斯牛顿法只能求解最小二乘问题，而公式（9）后面部分我理解为小量忽略了，另外，这里似乎是把$\sqrt{w_h}$看做了常数，不然$f(\mathbf{x})$在分界点就无法求导了。明确一下初始化过程要求解的参数：两帧图像的之间的相对位姿${\xi }_{21}$和光度参数$a,b$共8个参数，加上$N$个点在参考帧中的逆深度${\rho }_1$，共$N+8$个参数。由于后续求导时采用了扰动模型，这里设状态变量$\mathbf{x}=[{\rho }_1^{(1)},...,{\rho }_1^{(N)},{ϵ}^T,a,b{]}_{(N+8)\times 1}^T=[{\mathbf{x}}_{\alpha },{\mathbf{x}}_{\beta }{]}^T$，其中$ϵ$是位姿增量。

3.1 雅克比矩阵

3.1.1 光度参数求导

$$\frac{\partial f(\mathbf{x})}{\partial a}=-\sqrt{w_h}\exp (a)I_1({\mathbf{p}}_1)\text{\hspace{1em}(12)}$$
$$\frac{\partial f(\mathbf{x})}{\partial b}=-\sqrt{w_h}\text{\hspace{1em}(13)}$$

3.1.2 相对位姿求导

采用左乘扰动模型，对位姿的增量$ϵ$求导,根据链式法则：
$$\frac{\partial f(\mathbf{x})}{\partial ϵ}=\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}\frac{\partial {\mathbf{p}}_2}{\partial ϵ}\text{\hspace{1em}(14)}$$
设$▽I_x,▽I_y$分别为${\mathbf{p}}_2$处的水平和垂直方向上的梯度，则第一部分
$$\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}=\sqrt{w_h}\frac{\partial I_2({\mathbf{p}}_2)}{\partial {\mathbf{p}}_2}=\sqrt{w_h}\left[\begin{array}{cc}▽I_x& ▽I_y\end{array}\right]\text{\hspace{1em}(15)}$$
第二部分同样根据链式法则有：
$$\frac{\partial {\mathbf{p}}_2}{\partial ϵ}=\frac{\partial {\mathbf{p}}_2}{\partial {\mathbf{P}}_2}\frac{\partial {\mathbf{P}}_2}{\partial ϵ}\text{\hspace{1em}(16)}$$
其中，先看第一部分，关于像素坐标和空间坐标的关系，通过相机模型可知（见公式（1））
$$\left[\begin{array}{c}{u}_2\\ v_2\\ 1\end{array}\right]={\rho }_2\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_2\\ Y_2\\ Z_2\end{array}\right]\text{\hspace{1em}(17)}$$
这里${\rho }_2=1/Z_2$，${\mathbf{P}}_2=[X_2,Y_2,Z_2{]}^T$，因此不考虑齐次项的话，
$$\frac{\partial {\mathbf{p}}_2}{\partial {\mathbf{P}}_2}=\left[\begin{array}{ccc}\frac{\partial u_2}{\partial X_2}& \frac{\partial u_2}{\partial Y_2}& \frac{\partial u_2}{\partial Z_2}\\ \frac{\partial v_2}{\partial X_2}& \frac{\partial v_2}{\partial Y_2}& \frac{\partial v_2}{\partial Z_2}\end{array}\right]=\left[\begin{array}{ccc}{\rho }_2{f}_x& 0& -{\rho }_2^2{f}_x{X}_2\\ 0& {\rho }_2{f}_y& -{\rho }_2^2{f}_y{Y}_2\end{array}\right]\text{\hspace{1em}(18)}$$
然后考虑第二部分，根据左乘扰动模型，给定一个微小扰动$\Delta \mathbf{T}=exp(\delta {\xi }^{\wedge })$，其中$\delta \xi =[\delta \eta ,\delta \varphi {]}^T$，则
$$\begin{array}{rl}\frac{\partial {\mathbf{P}}_2}{\partial ϵ}& =\underset{\delta \xi \to 0}{\lim }\frac{exp(\delta {\xi }^{\wedge }){\mathbf{P}}_2-{\mathbf{P}}_2}{\delta \xi }\\ & \approx \underset{\delta \xi \to 0}{\lim }\frac{(\mathbf{I}+\delta {\xi }^{\wedge }){\mathbf{P}}_2-{\mathbf{P}}_2}{\delta \xi }\\ & =\underset{\delta \xi \to 0}{\lim }\frac{\delta {\xi }^{\wedge }{\mathbf{P}}_2}{\delta \xi }\\ & =\underset{\delta \xi \to 0}{\lim }\frac{\left[\begin{array}{cc}\delta {\varphi }^{\wedge }& \delta \eta \\ 0^T& 0\end{array}\right]\left[\begin{array}{c}{\mathbf{P}}_2\\ 1\end{array}\right]}{\delta \xi }\\ & =\left[\begin{array}{cc}\mathbf{I}& -{\mathbf{P}}_2^{\wedge }\\ 0^T& 0^T\end{array}\right]\end{array}\text{\hspace{1em}(19)}$$
注意中间有一次齐次变换，如果是非齐次式的形式的话，
$$\frac{\partial {\mathbf{P}}_2}{\partial ϵ}=\left[\begin{array}{cc}\mathbf{I}& -{\mathbf{P}}_2^{\wedge }\end{array}\right]=\left[\begin{array}{cccccc}1& 0& 0& 0& Z_2& -Y_2\\ 0& 1& 0& -Z_2& 0& X_2\\ 0& 0& 1& Y_2& -X_2& 0\end{array}\right]\text{\hspace{1em}(20)}$$
结合公式（18）和（20），公式（16）变为了
$$\begin{array}{rl}\frac{\partial {\mathbf{p}}_2}{\partial ϵ}& =\left[\begin{array}{cccccc}{\rho }_2{f}_x& 0& -{\rho }_2^2{f}_x{X}_2& -{\rho }_2^2{f}_x{X}_2{Y}_2& f_x+{\rho }_2^2{f}_x{X}_2^2& -{\rho }_2{f}_x{Y}_2\\ 0& {\rho }_2{f}_y& -{\rho }_2^2{f}_y{Y}_2& -f_y-{\rho }_2^2{f}_y{Y}_2^2& {\rho }_2^2{f}_y{X}_2{Y}_2& {\rho }_2{f}_y{x}_2\end{array}\right]\\ & =\left[\begin{array}{cccccc}{\rho }_2{f}_x& 0& -{\rho }_2{f}_x{u}_2^{\prime }& -f_x{u}_2^{\prime }{v}_2^{\prime }& f_x+f_x{u^{\prime }}_2^2& -f_x{v}_2^{\prime }\\ 0& {\rho }_2{f}_y& -{\rho }_2{f}_y{v}_2^{\prime }& -f_y-f_y{v^{\prime }}_2^2& f_y{u}_2^{\prime }{v}_2^{\prime }& f_y{u}_2^{\prime }\end{array}\right]\end{array}\text{\hspace{1em}(21)}$$
其中 $u_2^{\prime }=X_2/Z_2$，$v_2^{\prime }=Y_2/Z_2$，为归一化坐标。
结合公式（15）和（21），公式（14）变为了
$$\frac{\partial f(\mathbf{x})}{\partial ϵ}=\sqrt{w_h}{\left[\begin{array}{c}▽I_x{\rho }_2{f}_x\\ ▽I_y{\rho }_2{f}_y\\ -{\rho }_2(▽I_x{f}_x{u}_2^{\prime }-▽I_y{f}_y{v}_2^{\prime })\\ -▽I_x{f}_x{u}_2^{\prime }{v}_2^{\prime }-▽I_y{f}_y(1+{v^{\prime }}_2^2)\\ ▽I_x{f}_x(1+{u^{\prime }}_2^2)+▽I_y{f}_y{u}_2^{\prime }{v}_2^{\prime }\\ -▽I_x{f}_x{v}_2^{\prime }+▽I_y{f}_y{u}_2^{\prime }\end{array}\right]}^T\text{\hspace{1em}(22)}$$

3.1.3 逆深度求导

根据链式法则
$$\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}=\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}\frac{\partial {\mathbf{p}}_2}{\partial {\rho }_1}\text{\hspace{1em}(23)}$$
第一部分已有公式（15）给出，第二部分继续分解：
$$\frac{\partial {\mathbf{p}}_2}{\partial {\rho }_1}=\frac{\partial {\mathbf{p}}_2}{\partial {\mathbf{P}}_2}\frac{\partial {\mathbf{P}}_2}{\partial {\rho }_1}\text{\hspace{1em}(24)}$$
其中第一部分已经在式（18）中得到，现考虑第二部分，已知
$${\mathbf{P}}_2=\mathbf{R}{\mathbf{K}}^{-1}{\mathbf{P}}_1/{\rho }_1+\mathbf{t}\text{\hspace{1em}(25)}$$
则
$$\frac{\partial {\mathbf{P}}_2}{\partial {\rho }_1}=-\frac{\mathbf{R}{\mathbf{K}}^{-1}{\mathbf{P}}_1}{{\rho }_1^2}=-{\rho }_1^{-1}({\mathbf{P}}_2-\mathbf{t})=-{\rho }_1^{-1}{\left[\begin{array}{ccc}{X}_2-t_x& Y_2-t_y& Z_2-t_z\end{array}\right]}^T\text{\hspace{1em}(26)}$$
结合公式（18）和（26），公式（24）变为了
$$\frac{\partial {\mathbf{p}}_2}{\partial {\rho }_1}=-{\rho }_1^{-1}{\rho }_2\left[\begin{array}{c}{f}_x(u_2^{\prime }{t}_z-t_x)\\ f_y(v_2^{\prime }{t}_z-t_y)\end{array}\right]\text{\hspace{1em}(27)}$$
带入公式（23）得
$$\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}=\sqrt{w_h}{\rho }_1^{-1}{\rho }_2(▽I_x{f}_x(t_x-u_2^{\prime }{t}_z)+▽I_y{f}_y(t_y-v_2^{\prime }{t}_z))\text{\hspace{1em}(28)}$$
另外，并不是所有点都对逆深度求导的，代码中不断地对每一个点进行分类，判断当前点是否是一个足够好的点。基本逻辑如下：
（1） 所有点初始化时被标记为good；
（2） 在计算每个点的雅克比时，如果点落在平面外，bad；点落在平面内，但得到的残差和大于阈值，bad；
（3） 只有good的点的雅克比才会被归入到总的雅克比中参与增量方程的求解；
（4）在coarse到fine的过程中，每次开始时，如果bad的点在上一层中存在good的点，则继承该点（parent）的逆深度，并设为good；
（5） 在得到增量后，对good的点进行逆深度更新。


综上，我们已经得到了误差函数关于变量${\mathbf{x}}_{\alpha }$的雅克比矩阵${\mathbf{J}}_{\alpha }=[\frac{\partial f(\mathbf{x})}{\partial {\rho }_1^{(1)}},...,\frac{\partial f(\mathbf{x})}{\partial {\rho }_1^{(N)}}{]}_{1\times N}$，关于变量${\mathbf{x}}_{\beta }$的雅克比矩阵${\mathbf{J}}_{\beta }=[\frac{\partial f(\mathbf{x})}{\partial ϵ},\frac{\partial f(\mathbf{x})}{\partial a},\frac{\partial f(\mathbf{x})}{\partial b}{]}_{1\times 8}$，因此总的雅克比矩阵为$\mathbf{J}=[{\mathbf{J}}_{\alpha },{\mathbf{J}}_{\beta }{]}_{1\times (N+8)}$。

3.2 增量方程

将误差函数在当前状态一阶展开
$$f(\mathbf{x}+\Delta \mathbf{x})\approx f(\mathbf{x})+\mathbf{J}\Delta \mathbf{x}\text{\hspace{1em}(29)}$$
带入能量函数中，并对增量求微分
$$\frac{\partial \frac{1}{2}{f}^2(\mathbf{x}+\Delta \mathbf{x})}{\partial \Delta \mathbf{x}}=f(\mathbf{x}+\Delta \mathbf{x})\frac{\partial f(\mathbf{x}+\Delta \mathbf{x})}{\partial \Delta \mathbf{x}}\approx (f(\mathbf{x})+\mathbf{J}\Delta \mathbf{x})\mathbf{J}\text{\hspace{1em}(30)}$$
令该式等于0即得到增量方程
$${\mathbf{J}}^T\mathbf{J}\Delta \mathbf{x}=-{\mathbf{J}}^{T}f(\mathbf{x})\text{\hspace{1em}(31)}$$
令$\mathbf{H}=\sum {\mathbf{J}}^T\mathbf{J},\mathbf{g}=-\sum {\mathbf{J}}^{T}f(\mathbf{x})$，则增量方程变为
$$\mathbf{H}\Delta \mathbf{x}=\mathbf{g}\text{\hspace{1em}(32)}$$
求解增量方程就可以得到最优的增量$\Delta {\mathbf{x}}^{\ast }$，然后对状态进行更新，比如对相对位姿进行更新：
$$exp({\xi }_{21}^{\wedge })\leftarrow exp(\Delta {{{\mathbf{x}}_{\beta }}_{1:6}^{\ast }}^{\wedge })exp({\xi }_{21}^{\wedge })\text{\hspace{1em}(33)}$$
需要注意的是，DSO在初始化过程中似乎是固定了光度参数，没有对$a,b$进行更新。雅克比和误差计算的这一部分的代码主要在 CoarseInitializer::calcResAndGS 函数中。

3.3 增量方程的求解

增量方程可以表示为
$$\left[\begin{array}{cc}{\mathbf{H}}_{\alpha \alpha }& {\mathbf{H}}_{\alpha \beta }\\ {\mathbf{H}}_{\beta \alpha }& {\mathbf{H}}_{\beta \beta }\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{\alpha }\\ {\mathbf{x}}_{\beta }\end{array}\right]=\left[\begin{array}{c}{\mathbf{g}}_{\alpha }\\ {\mathbf{g}}_{\beta }\end{array}\right]\text{\hspace{1em}(34)}$$
其中，${\mathbf{H}}_{\alpha \alpha }=\sum {\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\alpha }$，${\mathbf{H}}_{\alpha \beta }=\sum {\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\beta }$，${\mathbf{H}}_{\beta \alpha }=\sum {\mathbf{J}}_{\beta }^T{\mathbf{J}}_{\alpha }$，${\mathbf{H}}_{\beta \beta }=\sum {\mathbf{J}}_{\beta }^T{\mathbf{J}}_{\beta }$，${\mathbf{g}}_{\alpha }=-\sum {\mathbf{J}}_{\alpha }^{T}f(\mathbf{x})$，${\mathbf{g}}_{\beta }=-\sum {\mathbf{J}}_{\beta }^{T}f(\mathbf{x})$。
通过Schur Complement进行消元：
$$\left[\begin{array}{cc}\mathbf{I}& 0\\ -{\mathbf{H}}_{\beta \alpha }{\mathbf{H}}_{\alpha \alpha }^{-1}& \mathbf{I}\end{array}\right]\left[\begin{array}{cc}{\mathbf{H}}_{\alpha \alpha }& {\mathbf{H}}_{\alpha \beta }\\ {\mathbf{H}}_{\beta \alpha }& {\mathbf{H}}_{\beta \beta }\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{\alpha }\\ {\mathbf{x}}_{\beta }\end{array}\right]=\left[\begin{array}{cc}\mathbf{I}& 0\\ -{\mathbf{H}}_{\beta \alpha }{\mathbf{H}}_{\alpha \alpha }^{-1}& \mathbf{I}\end{array}\right]\left[\begin{array}{c}{\mathbf{g}}_{\alpha }\\ {\mathbf{g}}_{\beta }\end{array}\right]\text{\hspace{1em}(35)}$$
$$\left[\begin{array}{cc}{\mathbf{H}}_{\alpha \alpha }& {\mathbf{H}}_{\alpha \beta }\\ 0& -{\mathbf{H}}_{\beta \alpha }{\mathbf{H}}_{\alpha \alpha }^{-1}{\mathbf{H}}_{\alpha \beta }+{\mathbf{H}}_{\beta \beta }\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{\alpha }\\ {\mathbf{x}}_{\beta }\end{array}\right]=\left[\begin{array}{c}{\mathbf{g}}_{\alpha }\\ -{\mathbf{H}}_{\beta \alpha }{\mathbf{H}}_{\alpha \alpha }^{-1}{\mathbf{g}}_{\alpha }+{\mathbf{g}}_{\beta }\end{array}\right]\text{\hspace{1em}(36)}$$
令${\mathbf{H}}_{\varphi }={\mathbf{H}}_{\beta \alpha }{\mathbf{H}}_{\alpha \alpha }^{-1}{\mathbf{H}}_{\alpha \beta }$，${\mathbf{g}}_{\varphi }={\mathbf{H}}_{\beta \alpha }{\mathbf{H}}_{\alpha \alpha }^{-1}{\mathbf{g}}_{\alpha }$，则
$${\mathbf{x}}_{\beta }={({\mathbf{H}}_{\beta \beta }-{\mathbf{H}}_{\varphi })}^{-1}({\mathbf{g}}_{\beta }-{\mathbf{g}}_{\varphi })\text{\hspace{1em}(37)}$$
$${\mathbf{x}}_{\alpha }={\mathbf{H}}_{\alpha \alpha }^{-1}({\mathbf{g}}_{\varphi }-{\mathbf{H}}_{\alpha \beta }{\mathbf{x}}_{\beta })\text{\hspace{1em}(38)}$$
因为${\mathbf{H}}_{\alpha \alpha }$是对角矩阵，它的逆就很好求了，也是对角矩阵，对角线上原先不为0倒一下。因此${\mathbf{H}}_{\varphi },{\mathbf{g}}_{\varphi }$也很好求了，可以直接通过累加的方式：
$${\mathbf{H}}_{\varphi }=\sum \frac{1}{{\mathbf{J}}_{\alpha }{\mathbf{J}}_{\alpha }^T}({\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\beta }{)}^T{\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\beta }\text{\hspace{1em}(39)}$$
$${\mathbf{g}}_{\varphi }=-\sum \frac{1}{{\mathbf{J}}_{\alpha }{\mathbf{J}}_{\alpha }^T}({\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\beta }{)}^T{\mathbf{J}}_{\alpha }^{T}f(\mathbf{x})\text{\hspace{1em}(40)}$$
这里的${\mathbf{H}}_{\varphi },{\mathbf{g}}_{\varphi }$就是代码中的Hsc,bsc，${\mathbf{H}}_{\beta \beta },{\mathbf{g}}_{\beta }$就是代码中的H,b，此外，DSO在迭代的过程中设置了一个参数lambda来调整下一次的迭代，类似于列文伯格方法中的$\lambda$：
$$(\mathbf{H}+\lambda {\mathbf{D}}^T\mathbf{D})\Delta \mathbf{x}=\mathbf{g}\text{\hspace{1em}(41)}$$
最后将得到的增量更新到状态变量上就完成了一次迭代过程。注意点的逆深度以及位姿中的平移分量最后要进行归一化操作。

4 初始化主要流程

参考文献
[1] Engel J, Koltun V, Cremers D. Direct sparse odometry[J]. IEEE transactions on pattern analysis and machine intelligence, 2018, 40(3): 611-625.
[2] 高翔. 视觉 SLAM 十四讲: 从理论到实践[M]. 电子工业出版社, 2017.
[3] JingeTU. 直接法光度误差导数推导[OL]. 博客园, 2018/01/05 [2019/05/24] http://www.cnblogs.com/JingeTU/p/8203606.html.
[4] JingeTU. DSO 优化代码中的 Schur Complement[OL]. 博客园, 2018/01/16 [2019/05/24] https://www.cnblogs.com/JingeTU/p/8297076.html.