DSO追踪与优化

与ORB-SLAM等不同，DSO在完成了初始化后，将追踪与优化都放在了主线程中，并通过采用滑动窗口法的方式来达到实时性，从这个角度来说，DSO可以看做是单线程的（当然内部有用到一些多线程操作）。
整个过程可以分为这几个步骤：

1 追踪

这部分主要代码在函数FullSystem::trackNewCoarse中。首先，DSO设置了一系列的候选位姿lastF_2_fh_tries，作为前一关键帧到当前帧的相对位姿的初值。这里主要参考前两帧和前一关键帧的位姿，就静止、恒定速度等猜想设了一些初值，另外主要针对旋转设置了许多微小的初始值。然后开始不断地尝试，从图像金字塔顶层开始就这些初值进行追踪CoarseTracker::trackNewestCoarse，如果找到一个合适的初值，就跳出循环。先来看一下追踪部分是如何实现的。函数CoarseTracker::trackNewestCoarse，传入参数有当前帧newFrameHessian，预测的相对位姿lastToNew_out，预测的相对光度aff_g2l_out（初始化为0），金字塔层数coarsestLvl，用来判断是否合适的误差minResForAbort，返回一个表明是否成功的bool值。该函数从输入的金字塔层级开始，由粗到精地计算最佳位姿。

1.1 误差计算

先是计算当前误差的大小CoarseTracker::calcRes。这一步里还没有改变位姿的大小，仅仅将前一关键帧的点按照预测值投影过来，然后将误差累计起来返回，并保存了后续计算雅克比矩阵需要的变量。这里和初始化时不同的是，追踪时已经有了一定的点，因此只考虑位姿加光度共８个参数。设误差函数
$$f(\mathbf{x})=I_2({\mathbf{p}}_2)-\exp (a)(I_1({\mathbf{p}}_1)-b_0)-b\text{\hspace{1em}(1)}$$
这里的$b_0$是参考帧（也就是这里的$I_1$）的$b$参数，由于求的是相对光度，本身对其他量的导数没有影响，放在这里我觉得是为了减小$a$的导数的大小，使系统更稳定？
对相对光度参数求导：
$$\frac{\partial f(\mathbf{x})}{\partial a}=\exp (a)(b_0-I_1({\mathbf{p}}_1))\text{\hspace{1em}(2)}$$
$$\frac{\partial f(\mathbf{x})}{\partial b}=-1\text{\hspace{1em}(3)}$$
同样的，对位姿增量求导（变量的含义见我上一篇博客《DSO初始化》）
$$\frac{\partial f(\mathbf{x})}{\partial ϵ}={\left[\begin{array}{c}▽I_x{\rho }_2{f}_x\\ ▽I_y{\rho }_2{f}_y\\ -{\rho }_2(▽I_x{f}_x{u}_2^{\prime }-▽I_y{f}_y{v}_2^{\prime })\\ -▽I_x{f}_x{u}_2^{\prime }{v}_2^{\prime }-▽I_y{f}_y(1+{v^{\prime }}_2^2)\\ ▽I_x{f}_x(1+{u^{\prime }}_2^2)+▽I_y{f}_y{u}_2^{\prime }{v}_2^{\prime }\\ -▽I_x{f}_x{v}_2^{\prime }+▽I_y{f}_y{u}_2^{\prime }\end{array}\right]}^T\text{\hspace{1em}(4)}$$
后续需要用到的变量保存在

buf_warped_idepth[numTermsInWarped] = new_idepth;　		//逆深度
buf_warped_u[numTermsInWarped] = u;	    		   		//归一化坐标u
buf_warped_v[numTermsInWarped] = v;	    		   		//归一化坐标v
buf_warped_dx[numTermsInWarped] = hitColor[1];  　　		//x方向梯度
buf_warped_dy[numTermsInWarped] = hitColor[2];  　　		//y方向梯度
buf_warped_residual[numTermsInWarped] = residual;  		//误差
buf_warped_weight[numTermsInWarped] = hw;　　　　　　		//Huber权重
buf_warped_refColor[numTermsInWarped] = lpc_color[i];	//参考帧中的灰度值

1.2 计算增量方程

接下来在函数CoarseTracker::calcGSSSE中计算增量方程中的$\mathbf{H}$和$\mathbf{g}$。上一节已经求得了对应变量的导数，它们在代码中的表示为

__m128 dx = _mm_mul_ps(_mm_load_ps(buf_warped_dx+i), fxl);
__m128 dy = _mm_mul_ps(_mm_load_ps(buf_warped_dy+i), fyl);
acc.updateSSE_eighted(
		_mm_mul_ps(id,dx),
		_mm_mul_ps(id,dy),
		_mm_sub_ps(zero, _mm_mul_ps(id,_mm_add_ps(_mm_mul_ps(u,dx), _mm_mul_ps(v,dy)))),
		_mm_sub_ps(zero, _mm_add_ps(
					_mm_mul_ps(_mm_mul_ps(u,v),dx),
					_mm_mul_ps(dy,_mm_add_ps(one, _mm_mul_ps(v,v))))),
		_mm_add_ps(
					_mm_mul_ps(_mm_mul_ps(u,v),dy),
					_mm_mul_ps(dx,_mm_add_ps(one, _mm_mul_ps(u,u)))),
		_mm_sub_ps(_mm_mul_ps(u,dy), _mm_mul_ps(v,dx)),
		_mm_mul_ps(a,_mm_sub_ps(b0, _mm_load_ps(buf_warped_refColor+i))),
		minusOne,
		_mm_load_ps(buf_warped_residual+i),
		_mm_load_ps(buf_warped_weight+i));

其中前８行对应雅克比矩阵$\mathbf{J}$，前面６个对应公式（４），第７、８行对应公式（２）、（３），第９行对应误差，第10行是Huber权重。然后就可以得到
$$\mathbf{H}={\mathbf{J}}^T\mathbf{W}\mathbf{J}\text{\hspace{1em}(5)}$$
$$\mathbf{g}=-{\mathbf{J}}^T\mathbf{W}f(\mathbf{x})\text{\hspace{1em}(6)}$$

1.3 迭代求解

首先，每一层的最大迭代次数是固定的，且各不相同，高层的次数多，低层的次数少

int maxIterations[] = {10,20,50,50,50};

初始的lambda设为0.01（即列文伯格方法中的拉格让日乘子$\lambda$），然后求解增量方程
$$(\mathbf{H}+\lambda \mathbf{I})\Delta \mathbf{x}=\mathbf{g}\text{\hspace{1em}(7)}$$
得到增量后对原来的状态变量进行更新
$$\mathbf{x}\leftarrow \mathbf{x}+\Delta \mathbf{x}\text{\hspace{1em}(8)}$$
注意位姿的更新不是李代数相加，而是指数映射到李群后相乘（因为前面求导时用的是扰动模型），代码如下所示：

SE3 refToNew_new = SE3::exp((Vec6)(incScaled.head<6>())) * refToNew_current;
AffLight aff_g2l_new = aff_g2l_current;
aff_g2l_new.a += incScaled[6];
aff_g2l_new.b += incScaled[7];

用新的状态变量重新计算误差，然后将新的误差和旧的误差做比较，考虑是否接受这次优化

bool accept = (resNew[0] / resNew[1]) < (resOld[0] / resOld[1]);

这里的resNew[0]是总的误差，resNew[1]是对应点的数量，当平均误差减小时，认为这次优化可以接受。如果可以接受，那么就缩小lambda（每次缩小为原来的二分之一），如果优化失败，那么就说明高斯牛顿法的二次函数近似效果在这里不太好，通过增大lambda（放大为原来的4倍）来改善。当某一次得到的增量小于一定值时，认为收敛了，迭代过程终止。
DSO通过比较前后两次误差的大小关系来判断，它要求每一次得到的结果至少要比上一次尝试（上一个候选位姿下的）好，否则就直接跳过；如果比上一次好，那么再看它是否小于设定的阈值，如果小的话就结束尝试。

2 关键帧决策

关键帧的选择主要考虑当前帧和前一关键帧在点的光流变化，不考虑旋转情况下的光流变化，曝光参数的变化，三者加权相加大于１时新建关键帧。

needToMakeKF = allFrameHistory.size()== 1 ||
					setting_kfGlobalWeight*setting_maxShiftWeightT *  sqrtf((double)tres[1]) / (wG[0]+hG[0]) +
					setting_kfGlobalWeight*setting_maxShiftWeightR *  sqrtf((double)tres[2]) / (wG[0]+hG[0]) +
					setting_kfGlobalWeight*setting_maxShiftWeightRT * sqrtf((double)tres[3]) / (wG[0]+hG[0]) +
					setting_kfGlobalWeight*setting_maxAffineWeight * fabs(logf((float)refToFh[0])) > 1 ||
					2*coarseTracker->firstCoarseRMSE < tres[0];

3 非关键帧

如果当前帧被认为是非关键帧，那么该帧就用来对活动窗口中所有的关键帧中还未成熟的点进行逆深度更新。基本原理是沿着极线进行搜索ImmaturePoint::traceOn。

3.1 极线搜索

首先，将未成熟的点根据相对位姿和之前的逆深度投影到当前帧上

Vec3f pr = hostToFrame_KRKi * Vec3f(u,v, 1);
Vec3f ptpMin = pr + hostToFrame_Kt*idepth_min;
float uMin = ptpMin[0] / ptpMin[2];
float vMin = ptpMin[1] / ptpMin[2];

这里的(uMin，vMin)就是设逆深度最小时投影得到的像素坐标。接下来确定极线，随便设一个逆深度0.01，得到另一个投影点的坐标(uMax，vMax)，

// project to arbitrary depth to get direction.
ptpMax = pr + hostToFrame_Kt*0.01;
uMax = ptpMax[0] / ptpMax[2];
vMax = ptpMax[1] / ptpMax[2];

这样就得到了极线的方向

// direction.
float dx = uMax-uMin;
float dy = vMax-vMin;
float d = 1.0f / sqrtf(dx*dx+dy*dy);

这样，极线可以表示为
(9) L : = { l 0 + λ [ l x , l y ] T } \mathbf L:=\{\mathbf l_0+\lambda[l_x, l_y]^T\} \tag{9} L:={l0​+λ[lx​,ly​]T}(9)
其中${\mathbf{l}}_0$就是[uMin，vMin]${}^T$，$\lambda$是离散的步长（视差），$[l_x,l_y{]}^T$表示极线的方向（单位向量）。
根据前面设的最大搜索范围，得到像素的最大范围

dist = maxPixSearch;
uMax = uMin + dist*dx*d;
vMax = vMin + dist*dy*d;

然后在最大范围内按一定步长进行离散搜索，找到最小的和第二小的误差，比较两者的比值。
最后在最小误差的位置上进行高斯牛顿优化（只有一个变量），每次迭代过程中如果误差大于前面得到的最小误差，就缩小优化步长重新来过，当增量小于一定值时停止。

3.2 逆深度范围更新

设
$${\mathbf{P}}_r=\mathbf{K}\mathbf{R}{\mathbf{K}}^{-1}{\left[\begin{array}{ccc}{u}_{\mathrm{１}}& v_1& 1\end{array}\right]}^T={\left[\begin{array}{ccc}{m}_1& m_2& m_3\end{array}\right]}^T\text{\hspace{1em}(9)}$$
$$\mathbf{K}\mathbf{t}={\left[\begin{array}{ccc}{n}_1& n_2& n_3\end{array}\right]}^T\text{\hspace{1em}(10)}$$
则投影后的像素坐标
$$u_2=\frac{m_1+n_1{\rho }_1}{m_3+n_3{\rho }_1}\text{\hspace{1em}(11)}$$
$$v_2=\frac{m_2+n_2{\rho }_1}{m_3+n_3{\rho }_1}\text{\hspace{1em}(12)}$$
把逆深度放在左边，
$${\rho }_1=\frac{m_3{u}_2-m_1}{n_1-n_3{u}_2}\text{\hspace{1em}(13)}$$
$${\rho }_1=\frac{m_3{v}_2-m_2}{n_2-n_3{v}_2}\text{\hspace{1em}(14)}$$
设$[u_2^{\ast },v_2^{\ast }{]}^T$为前面得到的最佳位置，并设当前像素位置的误差范围为$\alpha$，离散搜索的单位步长在ｘ,y方向上的投影分别为$\Delta u,\Delta v$，当ｘ方向梯度较大时，我们根据公式（13）来确定逆深度范围：
$${\rho }_{1min}=\frac{m_3(u_2^{\ast }-\alpha \Delta u)-m_1}{n_1-n_3(u_2^{\ast }-\alpha \Delta u)}\text{\hspace{1em}(15)}$$
$${\rho }_{1max}=\frac{m_3(u_2^{\ast }+\alpha \Delta u)-m_1}{n_1-n_3(u_2^{\ast }+\alpha \Delta u)}\text{\hspace{1em}(16)}$$
当y方向梯度较大时，根据公式（14）来确定逆深度范围：
$${\rho }_{1min}=\frac{m_3(v_2^{\ast }-\alpha \Delta v)-m_2}{n_2-n_3(v_2^{\ast }-\alpha \Delta v)}\text{\hspace{1em}(17)}$$
$${\rho }_{1max}=\frac{m_3(v_2^{\ast }+\alpha \Delta v)-m_2}{n_2-n_3(v_2^{\ast }+\alpha \Delta v)}\text{\hspace{1em}(18)}$$
相关代码

if(dx*dx>dy*dy)
{
	idepth_min = (pr[2]*(bestU-errorInPixel*dx) - pr[0]) / (hostToFrame_Kt[0] - hostToFrame_Kt[2]*(bestU-errorInPixel*dx));
	idepth_max = (pr[2]*(bestU+errorInPixel*dx) - pr[0]) / (hostToFrame_Kt[0] - hostToFrame_Kt[2]*(bestU+errorInPixel*dx));
}
else
{
	idepth_min = (pr[2]*(bestV-errorInPixel*dy) - pr[1]) / (hostToFrame_Kt[1] - hostToFrame_Kt[2]*(bestV-errorInPixel*dy));
	idepth_max = (pr[2]*(bestV+errorInPixel*dy) - pr[1]) / (hostToFrame_Kt[1] - hostToFrame_Kt[2]*(bestV+errorInPixel*dy));
}

接下来考虑$\alpha$。为什么这里要有个$\alpha$呢？前面通过离散搜索加上高斯牛顿优化的方式得到了最佳的匹配点，如果假设没有其他任何误差存在的话，我们完全可以令$\alpha ＝1$，这样逆深度的最大最小值就可以通过简单地扰动一个单位步长来得到。但考虑误差的话，我们会发现极线和梯度的夹角对结果有着非常大的影响。如果极线的方向和梯度的方向接近垂直的，那么稍微有一点位姿误差（必然存在）使得投影点和真实点产生了一定的误差，沿着极线搜索得到的结果就会产生巨大的偏差，如图１所示，具体分析可以参见参考文献[1, 3]。因此，非常有必要考虑这个$\alpha$，事实上，在代码中，$\alpha$的计算是在极线搜索之前做的，如果得到的$\alpha$太大（这意味这极线和梯度的夹角接近90度），就没有做极线搜索的必要。

图１　几何误差与极线和梯度的关系（来自文献[1]）

不过和文献[1]不同的是，DSO似乎没有直接根据公式计算视差的不确定度，$\alpha$更像是一个根据人工经验设计的置信系数（我目前是这么理解的，因为实在推不出这个公式），代码如下所示：

float dx = setting_trace_stepsize*(uMax-uMin);
float dy = setting_trace_stepsize*(vMax-vMin);

float a = (Vec2f(dx,dy).transpose() * gradH * Vec2f(dx,dy));
float b = (Vec2f(dy,-dx).transpose() * gradH * Vec2f(dy,-dx));
float errorInPixel = 0.2f + 0.2f * (a+b) / a;

令点在主导帧中的梯度雅克比为${\mathbf{J}}_{▽}=[▽x,▽y{]}^T$，gradH就是$\sum {\mathbf{J}}_{▽}{\mathbf{J}}_{▽}^T$，这里的求和符号表示对一个小块中的８个点求和，因此a则可以理解为极线与梯度的点乘的平方，b则可以理解为极线旋转90度后与梯度的点乘的平方，errorInPixel就是这里的$\alpha$。可以看到，errorInPixel基本来自于变量b/a，当b/a接近于0时（此时极线和梯度方向基本平行），$\alpha \approx 0.4$，逆深度只更新大约0.4个单位步长；而当b/a大于一定阈值时，则后续步骤直接跳过，该点被标记为IPS_BADCONDITION。

4 关键帧

如果当前帧被认为是关键帧，则进入函数FullSystem::makeKeyFrame：

1. 和非关键帧一样，利用当前帧对前面关键帧中的未成熟点进行逆深度更新FullSystem::traceNewCoarse；
2. 标记后面需要边缘化（从活动窗口踢出）的帧FullSystem::flagFramesForMarginalization；
3. 将当前帧加入到滑动窗口中frameHessians.push_back(fh)，并计算一下该窗口中其他帧与当前帧之间的一些参数比如相对光度、距离等FullSystem::setPrecalcValues；
4. 将当前帧加入到总的能量函数中EnergyFunctional（ef）；
5. 遍历窗口中之前所有帧的成熟点pointHessians，构建它们和新的关键帧的点帧误差PointFrameResidual，加入到ef中；
6. 激活窗口中之前所有帧中符合条件的未成熟点，将其加入到ef中FullSystem::activatePointsMT；
7. 利用高斯牛顿法对活动窗口中的所有变量进行优化FullSystem::optimize；
8. 去除外点FullSystem::removeOutliers；
9. 边缘化不需要的点EnergyFunctional::marginalizePointsF；
10. 在当前帧中提取未成熟点FullSystem::makeNewTraces；
11. 边缘化不需要的帧FullSystem::marginalizeFrame。

4.1 边缘化决策

主要两点（FullSystem::flagFramesForMarginalization）：

1. 当活跃的帧的数量大于最低要求（５个）时，边缘化一帧中活跃的点少于５%或者和最新的帧相比光度参数变化剧烈（$|a_1-a_2|>0.7$）的帧（从最早的帧开始遍历）；
2. 如果过程１没有找到需要边缘化的帧，则从全部帧中找到除最近的两帧外离当前帧最远的一帧。

4.2 点的激活

DSO代码中PointHessian表示可用于追踪和参与局部优化的点，除了初始化的第一帧外，它来源于每次生成关键帧时对未成熟点的提取FullSystem::makeNewTraces，并在后续关键帧生成时进行激活FullSystem::activatePointsMT，成功激活的点就由ImmaturePoint变为PointHessian，激活的基本步骤如下：

1. 根据当前窗口中已有的成熟点的数量ef->nPoints，设置激活阈值currentMinActDist；
2. 将所有的成熟点投影到当前帧，生成距离地图CoarseDistanceMap::makeDistanceMap（比如位置$\mathbf{p}$有一个投影点了，那么位置$\mathbf{p}$的值设为0，周围一圈像素设为１，再外面一圈设为２，以此类推，迭代进行）；
3. 遍历所有的未成熟点，如果满足一些条件比如上一次的投影轨迹长度（极线）小于8，quality（次最小误差比最小误差）大于3等，就将逆深度设为其最大值和最小值的平均，将其投影到当前帧，然后考虑其在距离地图上的值，如果该值足够大（用到了第一步中的激活阈值），可以认为该点附近没有成熟点，所以将其加入待优化序列里，反之，则删除该点；
4. 对待优化序列里的未成熟点进行优化FullSystem::activatePointsMT_Reductor，然后激活；

现在看一下这里对未成熟点是如何优化的。逆深度求导的过程和前一篇博客《DSO初始化》中的类似，不过这里还加入了一个和点的梯度有关的系数$w_p$，即《DSO初始化》中的公式（６）得到的结果。因为只有一个变量，雅克比矩阵就是所求得的导数：
$$J_{{\rho }_1}=\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}=w_p\sqrt{w_h}{\rho }_1^{-1}{\rho }_2(▽I_x{f}_x(t_x-u_2^{\prime }{t}_z)+▽I_y{f}_y(t_y-v_2^{\prime }{t}_z))\text{\hspace{1em}(19)}$$
后续的过程和第1.3章的一样，通过构建增量方程，求解得到最佳增量，最后更新逆深度。

4.3 滑动窗口法

DSO采用了滑动窗口法进行局部优化。滑动窗口法优化一个固定大小的关键帧序列（5到7帧），从而保证算法的优化时间不会随着时间的增长、关键帧的增多而变化，其误差函数的构成如图2所示。

图２　DSO误差构成的因子图表示（来自文献[２]）

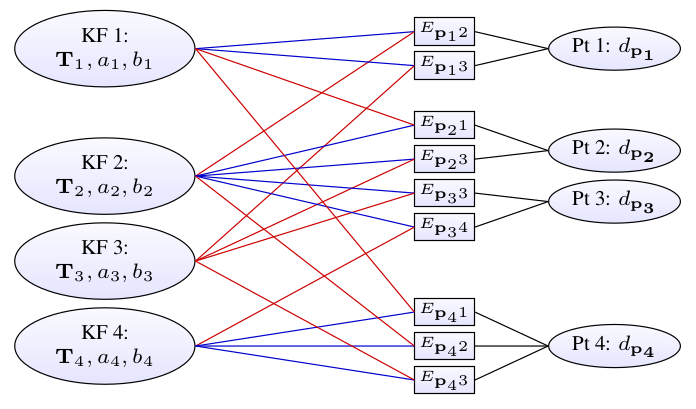
对每一组误差项所连接的主导帧 $i$ 和目标帧$j$，待优化的变量有主导帧和目标帧位姿、逆深度、相机参数$\mathbf{C}$（$f_x,f_y,c_x,c_y$）以及光度参数。关于位姿、逆深度和光度参数的求导前面都已给出，这里把相机参数的求导推一下。

4.4 相机参数求导

根据链式法则
$$\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}=\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}\frac{\partial {\mathbf{p}}_2}{\partial \mathbf{C}}\text{\hspace{1em}(20)}$$
其中第一项之前求过了，看第二项。由于$u_2=f_x{u}_2^{\prime }+c_x$，$v_2=f_y{v}_2^{\prime }+c_y$，
$$\begin{array}{rl}\frac{\partial {\mathbf{p}}_2}{\partial \mathbf{C}}& =\left[\begin{array}{cccc}\frac{\partial u_2}{\partial f_x}& \frac{\partial u_2}{\partial f_y}& \frac{\partial u_2}{\partial c_x}& \frac{\partial u_2}{\partial c_y}\\ \frac{\partial v_2}{\partial f_x}& \frac{\partial v_2}{\partial f_y}& \frac{\partial v_2}{\partial c_x}& \frac{\partial v_2}{\partial c_y}\end{array}\right]\\ & =\left[\begin{array}{cccc}{u}_2^{\prime }+f_x\frac{\partial u_2^{\prime }}{\partial f_x}& f_x\frac{\partial u_2^{\prime }}{\partial f_y}& f_x\frac{\partial u_2^{\prime }}{\partial c_x}+1& f_x\frac{\partial u_2^{\prime }}{\partial c_y}\\ f_y^{\prime }\frac{\partial v_2^{\prime }}{\partial f_x}& v_2^{\prime }+f_y\frac{\partial v_2^{\prime }}{\partial f_y}& f_y\frac{\partial v_2^{\prime }}{\partial c_x}& f_y\frac{\partial v_2^{\prime }}{\partial c_y}+1\end{array}\right]\end{array}\text{\hspace{1em}(21)}$$
其中
$$\begin{array}{rl}{\left[\begin{array}{ccc}{u}_2^{\prime }& v_2^{\prime }& 1\end{array}\right]}^T& ={\rho }_2(\mathbf{R}{\mathbf{P}}_1+\mathbf{t})\\ & ={\rho }_2({\rho }_1^{-1}\mathbf{R}{\mathbf{K}}^{-1}{\mathbf{p}}_1+\mathbf{t})\\ & ={\rho }_2{\rho }_1^{-1}\mathbf{R}{\mathbf{K}}^{-1}{\mathbf{p}}_1+{\rho }_2\mathbf{t}\\ & ={\rho }_2{\rho }_1^{-1}\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]\left[\begin{array}{ccc}{f}_x^{-1}& 0& -f_x^{-1}{c}_x\\ 0& f_y^{-1}& -f_y^{-1}{c}_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{u}_1\\ v_1\\ 1\end{array}\right]+{\rho }_2\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]\\ & ={\rho }_2{\rho }_1^{-1}\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]\left[\begin{array}{c}{f}_x^{-1}(u_1-c_x)\\ f_y^{-1}(v_1-c_y)\\ 1\end{array}\right]+{\rho }_2\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]\\ & ={\rho }_2{\rho }_1^{-1}\left[\begin{array}{c}{r}_{11}{f}_x^{-1}(u_1-c_x)+r_{12}{f}_y^{-1}(v_1-c_y)+r_{13}\\ r_{21}{f}_x^{-1}(u_1-c_x)+r_{22}{f}_y^{-1}(v_1-c_y)+r_{23}\\ r_{31}{f}_x^{-1}(u_1-c_x)+r_{32}{f}_y^{-1}(v_1-c_y)+r_{33}\end{array}\right]+{\rho }_2\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]\\ & ={\rho }_2{\rho }_1^{-1}\left[\begin{array}{c}{r}_{11}{f}_x^{-1}(u_1-c_x)+r_{12}{f}_y^{-1}(v_1-c_y)+r_{13}+{\rho }_1{t}_x\\ r_{21}{f}_x^{-1}(u_1-c_x)+r_{22}{f}_y^{-1}(v_1-c_y)+r_{23}+{\rho }_1{t}_y\\ r_{31}{f}_x^{-1}(u_1-c_x)+r_{32}{f}_y^{-1}(v_1-c_y)+r_{33}+{\rho }_1{t}_z\end{array}\right]\end{array}\text{\hspace{1em}(22)}$$
所以
$$u_2^{\prime }=\frac{r_{11}{f}_x^{-1}(u_1-c_x)+r_{12}{f}_y^{-1}(v_1-c_y)+r_{13}+{\rho }_1{t}_x}{r_{31}{f}_x^{-1}(u_1-c_x)+r_{32}{f}_y^{-1}(v_1-c_y)+r_{33}+{\rho }_1{t}_z}\text{\hspace{1em}(23)}$$
$$v_2^{\prime }=\frac{r_{21}{f}_x^{-1}(u_1-c_x)+r_{22}{f}_y^{-1}(v_1-c_y)+r_{23}+{\rho }_1{t}_y}{r_{31}{f}_x^{-1}(u_1-c_x)+r_{32}{f}_y^{-1}(v_1-c_y)+r_{33}+{\rho }_1{t}_z}\text{\hspace{1em}(24)}$$
分别进行求导可以得到（可参考文献[6]）
$$\frac{\partial u_2^{\prime }}{\partial f_x}={\rho }_2{\rho }_1^{-1}(r_{31}{u}_2^{\prime }-r_{11})f_x^{-2}(u_1-c_x)\text{\hspace{1em}(25)}$$
$$\frac{\partial u_2^{\prime }}{\partial f_y}={\rho }_2{\rho }_1^{-1}(r_{32}{u}_2^{\prime }-r_{12})f_y^{-2}(v_1-c_y)\text{\hspace{1em}(26)}$$
$$\frac{\partial u_2^{\prime }}{\partial c_x}={\rho }_2{\rho }_1^{-1}(r_{31}{u}_2^{\prime }-r_{11})f_x^{-1}\text{\hspace{1em}(27)}$$
$$\frac{\partial u_2^{\prime }}{\partial c_y}={\rho }_2{\rho }_1^{-1}(r_{32}{u}_2^{\prime }-r_{12})f_y^{-1}\text{\hspace{1em}(28)}$$
$$\frac{\partial v_2^{\prime }}{\partial f_x}={\rho }_2{\rho }_1^{-1}(r_{31}{v}_2^{\prime }-r_{21})f_x^{-2}(u_1-c_x)\text{\hspace{1em}(29)}$$
$$\frac{\partial v_2^{\prime }}{\partial f_y}={\rho }_2{\rho }_1^{-1}(r_{32}{v}_2^{\prime }-r_{22})f_y^{-2}(v_1-c_y)\text{\hspace{1em}(30)}$$
$$\frac{\partial v_2^{\prime }}{\partial c_x}={\rho }_2{\rho }_1^{-1}(r_{31}{v}_2^{\prime }-r_{21})f_x^{-1}\text{\hspace{1em}(31)}$$
$$\frac{\partial v_2^{\prime }}{\partial c_y}={\rho }_2{\rho }_1^{-1}(r_{32}{v}_2^{\prime }-r_{22})f_y^{-1}\text{\hspace{1em}(32)}$$
带入公式（21）可得（实现在PointFrameResidual::linearize中）
$$\frac{\partial {\mathbf{p}}_2}{\partial \mathbf{C}}=\left[\begin{array}{cccc}{u}_2^{\prime }+{\rho }_2{\rho }_1^{-1}{f}_x^{-1}(r_{31}{u}_2^{\prime }-r_{11})(u_1-c_x)& {\rho }_2{\rho }_1^{-1}{f}_x{f}_y^{-2}(r_{32}{u}_2^{\prime }-r_{12})(v_1-c_y)& {\rho }_2{\rho }_1^{-1}(r_{31}{u}_2^{\prime }-r_{11})+1& {\rho }_2{\rho }_1^{-1}{f}_x{f}_y^{-1}(r_{32}{u}_2^{\prime }-r_{12})\\ {\rho }_2{\rho }_1^{-1}{f}_x^{-2}{f}_y^{\prime }(r_{31}{v}_2^{\prime }-r_{21})(u_1-c_x)& v_2^{\prime }+{\rho }_2{\rho }_1^{-1}{f}_y^{-1}(r_{32}{v}_2^{\prime }-r_{22})(v_1-c_y)& {\rho }_2{\rho }_1^{-1}{f}_x^{-1}{f}_y(r_{31}{v}_2^{\prime }-r_{21})& {\rho }_2{\rho }_1^{-1}(r_{32}{v}_2^{\prime }-r_{22})+1\end{array}\right]\text{\hspace{1em}(33)}$$

4.5 相对位姿增量关于绝对位姿增量的导数

在前面初始化以及位姿追踪时，我们只需要求得相对位姿就可以了，然后根据前一关键帧的绝对位姿和求得的相对位姿得到当前帧的绝对位姿。但在局部优化的时候，最终优化的变量是活动窗口中每一关键帧的绝对位姿，而前面误差函数中我们只能看到相对位姿，因此需要对计算相对位姿增量关于绝对位姿增量的导数，以便于后面求解整个优化问题。
设某关联两帧（从host到target）的从世界坐标到相机坐标的变换矩阵分别为${\mathbf{T}}_{hw}$，${\mathbf{T}}_{tw}$，且${\mathbf{T}}_{th}={\mathbf{T}}_{tw}{\mathbf{T}}_{hw}^{-1}$，它们所对应的李代数增量分别为${ϵ}_{hw}$，${ϵ}_{tw}$，${ϵ}_{th}$。从前面的误差函数中，我们已经得到了$\frac{\partial \mathbf{f}(\mathbf{x})}{\partial {ϵ}_{th}}$，因此，要得到$\frac{\partial \mathbf{f}(\mathbf{x})}{\partial {ϵ}_{hw}}$和$\frac{\partial \mathbf{f}(\mathbf{x})}{\partial {ϵ}_{tw}}$，只需计算$\frac{\partial {ϵ}_{th}}{\partial {ϵ}_{hw}}$和$\frac{\partial {ϵ}_{th}}{\partial {ϵ}_{tw}}$。代码中这一步计算放在每次插入关键帧时的EnergyFunctional::setAdjointsF中，通过遍历两两之间的关系，提前计算好adHostF和adTargetF。

4.5.1 Adjoint

先介绍一下伴随（Adjoint），后面推导时要用到。一个$6\times 6$的变换矩阵$\mathcal{T}$，可以直接由一个$4\times 4$的变换矩阵$\mathbf{T}$构造给出：
$$\mathcal{T}=Ad(\mathbf{T})=Ad(\left[\begin{array}{cc}\mathbf{R}& \mathbf{t}\\ 0^T& 1\end{array}\right])=\left[\begin{array}{cc}\mathbf{R}& {\mathbf{t}}^{\wedge }\mathbf{R}\\ 0& \mathbf{R}\end{array}\right]\text{\hspace{1em}(34)}$$
$\mathcal{T}$被称为$SE(3)$元素$\mathbf{T}$的Adjoint，也是一个矩阵李群（详见参考文献[7]中7.1.4节）。有如下恒等式成立：
$$(\mathbf{T}\mathbf{p}{)}^{\odot }\equiv \mathbf{T}{\mathbf{p}}^{\odot }{\mathcal{T}}^{-1}\text{\hspace{1em}(35)}$$
$${\xi }^{\wedge }\mathbf{p}\equiv {\mathbf{p}}^{\odot }\xi \text{\hspace{1em}(36)}$$
其中，$\mathbf{p}=[X,Y,Z,1{]}^T=[\epsilon ,1{]}^T$是一个齐次坐标，操作符$\odot$表示:
$${\mathbf{p}}^{\odot }={\left[\begin{array}{cc}\mathbf{I}& -{\epsilon }^{\wedge }\\ 0^T& 0^T\end{array}\right]}_{4\times 6}\text{\hspace{1em}(37)}$$
公式（35）和（36）都容易证明，把各项展开即可。

4.5.2 $\frac{\partial {ϵ}_{th}}{\partial {ϵ}_{tw}}$

假设给${\mathbf{T}}_{tw}$一个扰动${ϵ}_{tw}$，对应的${\mathbf{T}}_{th}$产生了一个变动${ϵ}_{th}$，
$$exp({ϵ}_{th}^{\wedge }){\mathbf{T}}_{th}=exp({ϵ}_{tw}^{\wedge }){\mathbf{T}}_{tw}{\mathbf{T}}_{hw}^{-1}\text{\hspace{1em}(38)}$$
$$(\mathbf{I}+{ϵ}_{th}^{\wedge }){\mathbf{T}}_{th}=(\mathbf{I}+{ϵ}_{tw}^{\wedge }){\mathbf{T}}_{tw}{\mathbf{T}}_{hw}^{-1}=(\mathbf{I}+{ϵ}_{tw}^{\wedge }){\mathbf{T}}_{th}\text{\hspace{1em}(39)}$$
$${ϵ}_{th}={ϵ}_{tw}\text{\hspace{1em}(40)}$$
$$\frac{\partial {ϵ}_{th}}{\partial {ϵ}_{tw}}=\mathbf{I}\text{\hspace{1em}(41)}$$

4.5.3 $\frac{\partial {ϵ}_{th}}{\partial {ϵ}_{hw}}$

假设给${\mathbf{T}}_{hw}$一个扰动${ϵ}_{hw}$，对应的${\mathbf{T}}_{th}$产生了一个变动${ϵ}_{th}$，
$$exp({ϵ}_{th}^{\wedge }){\mathbf{T}}_{th}={\mathbf{T}}_{tw}(exp({ϵ}_{hw}^{\wedge }){\mathbf{T}}_{hw}{)}^{-1}={\mathbf{T}}_{tw}{\mathbf{T}}_{hw}^{-1}exp((-{ϵ}_{hw}{)}^{\wedge })\text{\hspace{1em}(42)}$$
$$(\mathbf{I}+{ϵ}_{th}^{\wedge }){\mathbf{T}}_{th}={\mathbf{T}}_{th}(\mathbf{I}-{ϵ}_{hw}^{\wedge })\text{\hspace{1em}(43)}$$
$${ϵ}_{th}^{\wedge }=-{\mathbf{T}}_{th}{ϵ}_{hw}^{\wedge }{\mathbf{T}}_{th}^{-1}\text{\hspace{1em}(44)}$$
两边同乘一个点的齐次坐标
$${ϵ}_{th}^{\wedge }\mathbf{p}=-{\mathbf{T}}_{th}{ϵ}_{hw}^{\wedge }{\mathbf{T}}_{th}^{-1}\mathbf{p}\text{\hspace{1em}(45)}$$
根据公式（36）
$${\mathbf{p}}^{\odot }{ϵ}_{th}=-{\mathbf{T}}_{th}({\mathbf{T}}_{th}^{-1}\mathbf{p}{)}^{\odot }{ϵ}_{hw}\text{\hspace{1em}(46)}$$
根据公式（35）
$${\mathbf{p}}^{\odot }{ϵ}_{th}=-{\mathbf{T}}_{th}{\mathbf{T}}_{th}^{-1}{\mathbf{p}}^{\odot }{\mathcal{T}}^{-1}{ϵ}_{hw}=-{\mathbf{p}}^{\odot }{\mathcal{T}}^{-1}{ϵ}_{hw}\text{\hspace{1em}(47)}$$
因此
$${ϵ}_{th}=-{\mathcal{T}}^{-1}{ϵ}_{hw}\text{\hspace{1em}(48)}$$
$$\frac{\partial {ϵ}_{th}}{\partial {ϵ}_{hw}}=-{\mathcal{T}}^{-1}\text{\hspace{1em}(49)}$$

4.6 增量方程

考虑一下变量的数量。设有$N$个关键帧参与优化，其中包含$M$个点和$K$个误差项（显然$M\le K$），这样待优化的参数有$M+8\times N+4$，其中8表示了6个位姿变量和2个光度参数，4表示了4个相机内参。当系统稳定运行时，最多有8个关键帧同时存在于滑动窗口内，此时有$M+68$个变量。设前者（点）的近似Hessian矩阵为${\mathbf{H}}_{\alpha \alpha }$，后者为${\mathbf{H}}_{\beta \beta }$，增量方程变为
$$\left[\begin{array}{cc}{\mathbf{H}}_{\alpha \alpha }& {\mathbf{H}}_{\alpha \beta }\\ {\mathbf{H}}_{\beta \alpha }& {\mathbf{H}}_{\beta \beta }\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{\alpha }\\ {\mathbf{x}}_{\beta }\end{array}\right]=\left[\begin{array}{c}{\mathbf{g}}_{\alpha }\\ {\mathbf{g}}_{\beta }\end{array}\right]\text{\hspace{1em}(50)}$$
利用Schur Complement进行消元可以得到
$${\mathbf{x}}_{\beta }={({\mathbf{H}}_{\beta \beta }-{\mathbf{H}}_{\varphi })}^{-1}({\mathbf{g}}_{\beta }-{\mathbf{g}}_{\varphi })\text{\hspace{1em}(51)}$$
$${\mathbf{x}}_{\alpha }={\mathbf{H}}_{\alpha \alpha }^{-1}({\mathbf{g}}_{\varphi }-{\mathbf{H}}_{\alpha \beta }{\mathbf{x}}_{\beta })\text{\hspace{1em}(52)}$$
其中
$${\mathbf{H}}_{\varphi }=\frac{1}{{\mathbf{J}}_{\alpha }{\mathbf{J}}_{\alpha }^T}({\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\beta }{)}^T{\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\beta }\text{\hspace{1em}(53)}$$
$${\mathbf{g}}_{\varphi }=-\frac{1}{{\mathbf{J}}_{\alpha }{\mathbf{J}}_{\alpha }^T}({\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\beta }{)}^T{\mathbf{J}}_{\alpha }^{T}f(\mathbf{x})\text{\hspace{1em}(54)}$$

4.7 对应代码

来看一下实际代码中是怎么构建增量方程以及求解优化的。从FullSystem::optimize进入后，首先通过FullSystem::linearizeAll计算相关的导数。

4.7.1 逆深度$\frac{\partial {\mathbf{p}}_2}{\partial {\rho }_1}$

d_d_x = drescale * (PRE_tTll_0[0]-PRE_tTll_0[2]*u)*SCALE_IDEPTH*HCalib->fxl();
d_d_y = drescale * (PRE_tTll_0[1]-PRE_tTll_0[2]*v)*SCALE_IDEPTH*HCalib->fyl();

J->Jpdd[0] = d_d_x;
J->Jpdd[1] = d_d_y;

$$\frac{\partial {\mathbf{p}}_2}{\partial {\rho }_1}=-{\rho }_1^{-1}{\rho }_2\left[\begin{array}{c}{f}_x(u_2^{\prime }{t}_z-t_x)\\ f_y(v_2^{\prime }{t}_z-t_y)\end{array}\right]\text{\hspace{1em}(55)}$$

4.7.2 相机内参$\frac{\partial {\mathbf{p}}_2}{\partial \mathbf{C}}$

d_C_x[2] = drescale*(PRE_RTll_0(2,0)*u-PRE_RTll_0(0,0));
d_C_x[3] = HCalib->fxl() * drescale*(PRE_RTll_0(2,1)*u-PRE_RTll_0(0,1)) * HCalib->fyli();
d_C_x[0] = KliP[0]*d_C_x[2];
d_C_x[1] = KliP[1]*d_C_x[3];

d_C_y[2] = HCalib->fyl() * drescale*(PRE_RTll_0(2,0)*v-PRE_RTll_0(1,0)) * HCalib->fxli();
d_C_y[3] = drescale*(PRE_RTll_0(2,1)*v-PRE_RTll_0(1,1));
d_C_y[0] = KliP[0]*d_C_y[2];
d_C_y[1] = KliP[1]*d_C_y[3];

d_C_x[0] = (d_C_x[0]+u)*SCALE_F;
d_C_x[1] *= SCALE_F;
d_C_x[2] = (d_C_x[2]+1)*SCALE_C;
d_C_x[3] *= SCALE_C;

d_C_y[0] *= SCALE_F;
d_C_y[1] = (d_C_y[1]+v)*SCALE_F;
d_C_y[2] *= SCALE_C;
d_C_y[3] = (d_C_y[3]+1)*SCALE_C;

J->Jpdc[0] = d_C_x;
J->Jpdc[1] = d_C_y;

对应公式（33）。

4.7.3 位姿增量$\frac{\partial {\mathbf{p}}_2}{\partial ϵ}$

d_xi_x[0] = new_idepth*HCalib->fxl();
d_xi_x[1] = 0;
d_xi_x[2] = -new_idepth*u*HCalib->fxl();
d_xi_x[3] = -u*v*HCalib->fxl();
d_xi_x[4] = (1+u*u)*HCalib->fxl();
d_xi_x[5] = -v*HCalib->fxl();

d_xi_y[0] = 0;
d_xi_y[1] = new_idepth*HCalib->fyl();
d_xi_y[2] = -new_idepth*v*HCalib->fyl();
d_xi_y[3] = -(1+v*v)*HCalib->fyl();
d_xi_y[4] = u*v*HCalib->fyl();
d_xi_y[5] = u*HCalib->fyl();

J->Jpdxi[0] = d_xi_x;
J->Jpdxi[1] = d_xi_y;

$$\frac{\partial {\mathbf{p}}_2}{\partial ϵ}=\left[\begin{array}{cccccc}{\rho }_2{f}_x& 0& -{\rho }_2{f}_x{u}_2^{\prime }& -f_x{u}_2^{\prime }{v}_2^{\prime }& f_x+f_x{u^{\prime }}_2^2& -f_x{v}_2^{\prime }\\ 0& {\rho }_2{f}_y& -{\rho }_2{f}_y{v}_2^{\prime }& -f_y-f_y{v^{\prime }}_2^2& f_y{u}_2^{\prime }{v}_2^{\prime }& f_y{u}_2^{\prime }\end{array}\right]\text{\hspace{1em}(56)}$$

4.7.4 图像梯度$\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}$

if(hw < 1) hw = sqrtf(hw);

hitColor[1]*=hw;
hitColor[2]*=hw;
			
J->JIdx[0][idx] = hitColor[1];
J->JIdx[1][idx] = hitColor[2];

$$\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}=\sqrt{w_h}\left[\begin{array}{cc}▽I_x& ▽I_y\end{array}\right]\text{\hspace{1em}(57)}$$

4.7.5 光度参数 $\mathbf{A}=[a,b{]}^T$

float b0 = precalc->PRE_b0_mode;

float drdA = (color[idx]-b0);

J->JabF[0][idx] = drdA*hw;
J->JabF[1][idx] = hw;

这里和公式（2）、（3）中有点不同。追踪的时候只需要考虑如何得到最佳的相对光度的增量，因为当前帧的光度参数是未知的，而局部优化时每一帧都已经有光度参数了，而且都需要进行优化，因此类似于第4.5节的内容，可以事先算好相对量对绝对量的导数，然后这里计算相对光度的导数，最后构造Hessian矩阵时再加起来，只要最终的导数是正确的就行了。根据代码来看，误差函数和相对光度的关系（这里先忽略一下权重系数）
$$f(\mathbf{x})=I_t+a(I_h-b_0)+b\text{\hspace{1em}(58)}$$
而根据论文中的公式（4），误差函数应该是
$$f(\mathbf{x})=I_t-b_t-\exp (a_t-a_h)(I_h-b_h)\text{\hspace{1em}(59)}$$
根据对应关系可以得到

$$[\frac{\partial a}{\partial a_h},\frac{\partial b}{\partial b_h}]=[\exp (a_t-a_h),\exp (a_t-a_h)]\text{\hspace{1em}(60)}$$
$$[\frac{\partial a}{\partial a_t},\frac{\partial b}{\partial b_t}]=[-\exp (a_t-a_h),-1]\text{\hspace{1em}(61)}$$
和前面函数EnergyFunctional::setAdjointsF中设置的

Vec2f affLL = AffLight::fromToVecExposure(host->ab_exposure, target->ab_exposure, host->aff_g2l_0(), target->aff_g2l_0()).cast<float>();
AT(6,6) = -affLL[0];
AH(6,6) = affLL[0];
AT(7,7) = -1;
AH(7,7) = affLL[0];

一致。这里的affLL[0]就是$\exp (a_t-a_h)$。

4.7.6 一些中间量

退出FullSystem::linearizeAll后，进入函数FullSystem::applyRes_Reductor中，在EFResidual::takeDataF中设置了一些后续要用到的中间变量：

Vec2f JI_JI_Jd = J->JIdx2 * J->Jpdd;

for(int i=0;i<6;i++)
	JpJdF[i] = J->Jpdxi[0][i]*JI_JI_Jd[0] + J->Jpdxi[1][i] * JI_JI_Jd[1];

JpJdF.segment<2>(6) = J->JabJIdx*J->Jpdd;

其中Jpdxi表示$\frac{\partial {\mathbf{p}}_2}{\partial ϵ}$，Jpdd表示$\frac{\partial {\mathbf{p}}_2}{\partial {\rho }_1}$，JabJIdx表示$(\frac{\partial f(\mathbf{x})}{\partial \mathbf{A}}{)}^T\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}$，JIdx2表示$(\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}{)}^T\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}$，因此JI_JI_Jd为$(\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}{)}^T\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}$，JpJdF前6项表示$(\frac{\partial f(\mathbf{x})}{\partial ϵ}{)}^T\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}$，后2项表示$(\frac{\partial f(\mathbf{x})}{\partial \mathbf{A}}{)}^T\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}$。

4.7.7 Hessian矩阵的构成

在完成相关导数计算后，算法进入优化循环。首先，通过FullSystem::backupState保存当前的状态，这是为了在优化结果不好的情况下可以回退。然后求解优化增量FullSystem::solveSystem，这主要在EnergyFunctional::solveSystemF中实现。在求解之前，先看一下Hessian矩阵是怎么构成的。

4.7.7.1 ${\mathbf{H}}_{\beta \beta }$

MatXX HL_top, HA_top, H_sc;
VecX  bL_top, bA_top, bM_top, b_sc;

accumulateAF_MT(HA_top, bA_top,multiThreading);
accumulateLF_MT(HL_top, bL_top,multiThreading);
accumulateSCF_MT(H_sc, b_sc,multiThreading);

bM_top = (bM+ HM * getStitchedDeltaF());

先来看一下EnergyFunctional::accumulateAF_MT做了些什么，看名字像是累积active点的Hessian矩阵信息，MT是多线程的意思。在函数AccumulatedTopHessianSSE::addPoint中，

if(mode==0)
	resApprox = rJ->resF;
for(int i=0;i<patternNum;i++)
{
	JI_r[0] += resApprox[i] *rJ->JIdx[0][i];
	JI_r[1] += resApprox[i] *rJ->JIdx[1][i];
	Jab_r[0] += resApprox[i] *rJ->JabF[0][i];
	Jab_r[1] += resApprox[i] *rJ->JabF[1][i];
	rr += resApprox[i]*resApprox[i];
}

resApprox是$8\times 1$的误差向量（这里暂且只考虑mode为0的情况），因此这里的JI_r为$\sum (\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}{)}^{T}f(\mathbf{x})$，Jab_r为$\sum (\frac{\partial f(\mathbf{x})}{\partial \mathbf{A}}{)}^{T}f(\mathbf{x})$，rr是误差和的平方。

acc[tid][htIDX].update(
		rJ->Jpdc[0].data(), rJ->Jpdxi[0].data(),
		rJ->Jpdc[1].data(), rJ->Jpdxi[1].data(),
		rJ->JIdx2(0,0),rJ->JIdx2(0,1),rJ->JIdx2(1,1));

acc[tid][htIDX].updateBotRight(
		rJ->Jab2(0,0), rJ->Jab2(0,1), Jab_r[0],
		rJ->Jab2(1,1), Jab_r[1],rr);

acc[tid][htIDX].updateTopRight(
		rJ->Jpdc[0].data(), rJ->Jpdxi[0].data(),
		rJ->Jpdc[1].data(), rJ->Jpdxi[1].data(),
		rJ->JabJIdx(0,0), rJ->JabJIdx(0,1),
		rJ->JabJIdx(1,0), rJ->JabJIdx(1,1),
		JI_r[0], JI_r[1]);

这里暂且忽略多线程实现方面的细节。打开acc所在的类AccumulatorApprox，找到类内变量Mat1313f H;，可以看出一个$13\times 13$的矩阵。H是在其类内函数AccumulatorApprox::finish中构成的，可以从中发现其可以分成3个部分Data1m，BotRight_Data1m，TopRight_Data1m，正好对应上面三个update的函数。
$${\mathbf{H}}_{top}^A=\left[\begin{array}{cc}{{\mathbf{H}}_a}_{10\times 10}& {{\mathbf{H}}_b}_{10\times 3}\\ {{\mathbf{H}}_b}_{3\times 10}^T& {{\mathbf{H}}_c}_{3\times 3}\end{array}\right]\text{\hspace{1em}(62)}$$
根据输入的变量，可以知道
$${{\mathbf{H}}_a}_{10\times 10}=\left[\begin{array}{cc}{(\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}{)}^T\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}}_{4\times 4}& {(\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}{)}^T\frac{\partial f(\mathbf{x})}{\partial ϵ}}_{4\times 6}\\ {(\frac{\partial f(\mathbf{x})}{\partial ϵ}{)}^T\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}}_{6\times 4}& {(\frac{\partial f(\mathbf{x})}{\partial ϵ}{)}^T\frac{\partial f(\mathbf{x})}{\partial ϵ}}_{6\times 6}\end{array}\right]\text{\hspace{1em}(63)}$$
$${{\mathbf{H}}_b}_{10\times 3}=\left[\begin{array}{cc}{(\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}{)}^T\frac{\partial f(\mathbf{x})}{\partial \mathbf{A}}}_{4\times 2}& {(\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}{)}^{T}f(\mathbf{x})}_{4\times 1}\\ {(\frac{\partial f(\mathbf{x})}{\partial ϵ}{)}^T\frac{\partial f(\mathbf{x})}{\partial \mathbf{A}}}_{6\times 2}& {(\frac{\partial f(\mathbf{x})}{\partial ϵ}{)}^{T}f(\mathbf{x})}_{6\times 1}\end{array}\right]\text{\hspace{1em}(64)}$$
$${{\mathbf{H}}_c}_{3\times 3}=\left[\begin{array}{cc}{(\frac{\partial f(\mathbf{x})}{\partial \mathbf{A}}{)}^T\frac{\partial f(\mathbf{x})}{\partial \mathbf{A}}}_{2\times 2}& {(\frac{\partial f(\mathbf{x})}{\partial \mathbf{A}}{)}^{T}f(\mathbf{x})}_{2\times 1}\\ {f(\mathbf{x}{)}^T\frac{\partial f(\mathbf{x})}{\partial \mathbf{A}}}_{1\times 2}& {f(\mathbf{x}{)}^{T}f(\mathbf{x})}_{1\times 1}\end{array}\right]\text{\hspace{1em}(65)}$$
所对应的的雅克比矩阵为
$${\mathbf{J}}_{\beta }={\left[\begin{array}{ccc}\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}& \frac{\partial f(\mathbf{x})}{\partial ϵ}& \frac{\partial f(\mathbf{x})}{\partial \mathbf{A}}\end{array}\right]}_{8\times 12}\text{\hspace{1em}(66)}$$
把位姿和光度放在一起表示为一个8维的向量$\psi$，则雅克比变为
$${\mathbf{J}}_{\beta }={\left[\begin{array}{cc}\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}& \frac{\partial f(\mathbf{x})}{\partial \psi }\end{array}\right]}_{8\times 12}\text{\hspace{1em}(67)}$$

Vec2f Ji2_Jpdd = rJ->JIdx2 * rJ->Jpdd;
bd_acc +=  JI_r[0]*rJ->Jpdd[0] + JI_r[1]*rJ->Jpdd[1];
Hdd_acc += Ji2_Jpdd.dot(rJ->Jpdd);
Hcd_acc += rJ->Jpdc[0]*Ji2_Jpdd[0] + rJ->Jpdc[1]*Ji2_Jpdd[1];

这里Ji2_Jpdd表示$(\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_2}{)}^T\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}$，bd_acc表示$\sum f(\mathbf{x})\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}$，Hdd_acc表示$\sum (\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}{)}^T\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}$，Hcd_acc表示$\sum (\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}{)}^T\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}$，这些是EFPoint的成员变量，用来在后面优化点的逆深度。
接着进入函数AccumulatedTopHessianSSE::stitchDoubleMT，在AccumulatedTopHessianSSE::stitchDoubleInternal中，遍历多个线程，调用了acc的finish函数得到Hessian矩阵。注意这个Hessian矩阵只关联两帧的相对信息，并不是最终的结果。

H[tid].block<8,8>(hIdx, hIdx).noalias() += EF->adHost[aidx] * accH.block<8,8>(CPARS,CPARS) * EF->adHost[aidx].transpose();
H[tid].block<8,8>(tIdx, tIdx).noalias() += EF->adTarget[aidx] * accH.block<8,8>(CPARS,CPARS) * EF->adTarget[aidx].transpose();

这里的H是一个$68\times 68$的矩阵（假设系统已稳定，当前滑动窗口中有8个关键帧），其中左上角$4\times 4$的小块是关于相机内参的。这里通过遍历将每条边所属的Hessian信息加入到总的Hessian矩阵中，这里的EF->adHost和EF->adTarget分别表示第4.5节所计算得到的$\frac{\partial {ϵ}_{th}}{\partial {ϵ}_{hw}}$，$\frac{\partial {ϵ}_{th}}{\partial {ϵ}_{tw}}$（以及第4.7.5提到的光度信息），这样就把前面acc里得到的相对位姿的信息转变为绝对位姿的信息。accumulateLF_MT暂且不提，后面分析边缘化时再看。

4.7.7.2 ${\mathbf{H}}_{\varphi }$

accumulateSCF_MT是计算Schur Complement部分的矩阵，也就是公式（53）（54）的内容。

float H = p->Hdd_accAF+p->Hdd_accLF+p->priorF;
VecCf Hcd = p->Hcd_accAF + p->Hcd_accLF;

Hdd_accAF是$\sum (\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}{)}^T\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}$，Hcd_accAF是$\sum (\frac{\partial f(\mathbf{x})}{\partial \mathbf{C}}{)}^T\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}$（见第4.7.7.1节）

accHcc[tid].update(Hcd,Hcd,p->HdiF);
accbc[tid].update(Hcd, p->bdSumF * p->HdiF);

accHcc是一个$4\times 4$矩阵，相当于累计了${\mathbf{H}}_{\varphi }$的内参部分的信息$\frac{1}{{\mathbf{J}}_{\alpha }{\mathbf{J}}_{\alpha }^T}({\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\mathbf{C}}{)}^T{\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\mathbf{C}}$，accbc是一个$4\times 1$的矩阵，累计了${\mathbf{g}}_{\varphi }$的内参部分的信息$\frac{1}{{\mathbf{J}}_{\alpha }{\mathbf{J}}_{\alpha }^T}({\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\mathbf{C}}{)}^T{\mathbf{J}}_{\alpha }^{T}f(\mathbf{x})$。

accD[tid][r1ht+r2->targetIDX*nFrames2].update(r1->JpJdF, r2->JpJdF, p->HdiF);

JpJdF表示$(\frac{\partial f(\mathbf{x})}{\partial \psi }{)}^T\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}$，accD是一个$8\times 8$矩阵，相当于累计了${\mathbf{H}}_{\varphi }$的位姿和光度部分的信息$\frac{1}{{\mathbf{J}}_{\alpha }{\mathbf{J}}_{\alpha }^T}({\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\psi }{)}^T{\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\psi }$。

accE[tid][r1ht].update(r1->JpJdF, Hcd, p->HdiF);

accE是一个$8\times 4$矩阵，$\frac{1}{{\mathbf{J}}_{\alpha }{\mathbf{J}}_{\alpha }^T}({\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\psi }{)}^T{\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\mathbf{C}}$。

accEB[tid][r1ht].update(r1->JpJdF,p->HdiF*p->bdSumF);

accEB是一个$8\times 1$矩阵，$\frac{1}{{\mathbf{J}}_{\alpha }{\mathbf{J}}_{\alpha }^T}({\mathbf{J}}_{\alpha }^T{\mathbf{J}}_{\psi }{)}^T{\mathbf{J}}_{\alpha }^{T}f(\mathbf{x})$。

accE[tid2][ijIdx].finish();
accEB[tid2][ijIdx].finish();
Hpc += accE[tid2][ijIdx].A1m.cast<double>();
bp += accEB[tid2][ijIdx].A1m.cast<double>();

然后进入AccumulatedSCHessianSSE::stitchDoubleInternal将这些信息综合起来，

H[tid].block<8,CPARS>(iIdx,0) += EF->adHost[ijIdx] * Hpc;
H[tid].block<8,CPARS>(jIdx,0) += EF->adTarget[ijIdx] * Hpc;
b[tid].segment<8>(iIdx) += EF->adHost[ijIdx] * bp;
b[tid].segment<8>(jIdx) += EF->adTarget[ijIdx] * bp;

H[tid].block<8,8>(iIdx, iIdx) += EF->adHost[ijIdx] * accDM * EF->adHost[ikIdx].transpose();
H[tid].block<8,8>(jIdx, kIdx) += EF->adTarget[ijIdx] * accDM * EF->adTarget[ikIdx].transpose();
H[tid].block<8,8>(jIdx, iIdx) += EF->adTarget[ijIdx] * accDM * EF->adHost[ikIdx].transpose();
H[tid].block<8,8>(iIdx, kIdx) += EF->adHost[ijIdx] * accDM * EF->adTarget[ikIdx].transpose();

注意同上一节一样，需要将相对信息转变为绝对信息。这样就得到了${\mathbf{H}}_{\varphi }$和${\mathbf{g}}_{\varphi }$。

4.8 迭代更新

求解完增量方程后，和前面追踪时的套路相似，对变量进行更新，然后重新计算一次能量函数，如果确实是下降的，说明这次优化有效，保存后缩小lambda的值，继续迭代直到收敛，否则进行回滚。
每一次优化时增量的更新在EnergyFunctional::resubstituteF_MT中完成，其中点的逆深度增量的更新在EnergyFunctional::resubstituteFPt中（公式（52）就是在这里实现的）。增量方程求解完后，在FullSystem::doStepFromBackup中对变量进行更新，并通过评估本次增量的大小来判断是否结束迭代。

4.9 边缘化 Marginalization

在前面AccumulatedTopHessianSSE::addPoint中，其实函数就点的三种不同状态累计Hessian矩阵的信息，分别是active（也就是前面介绍的部分），linearized，和marginalized三种状态。后面两种状态都和Marginalization有关，因此放到这里来讨论。关于Marginalization，可以参见博客[8]，这里简单阐述一下，重点放在DSO代码实现部分。滑动窗口法维护了一个固定大小的关键帧序列以及相应的点，对应的误差信息放在一个Hessian矩阵中，局部优化的过程其实就是维护这个Hessian矩阵。因此，当有关键帧和点需要被丢掉时，这里就有一个信息的取舍问题。这些即将离开滑动窗口的变量，他们和现在仍在滑动窗口中的其他量之间存在一定的联系（误差），如果简单地忽略掉，显然会丢失信息。因此Marginalization的作用就是保留这些信息（约束），并将其作为后续优化过程中的先验信息。但也不是所有信息都保留，DSO中提到"To preserve the sparsity structure of the Hessian, all observations of still existing points in the frame are dropped from the system."也就是说，出于效率考虑（防止Hessian矩阵变得过于稠密），有些观测值是直接被舍弃的。

4.9.1 点的边缘化决策

关于关键帧的边缘化决策在第4.1节已经介绍了，现在先来看一下点的边缘化决策。在优化完成并去除外点FullSystem::removeOutliers后，程序先进入FullSystem::flagPointsForRemoval。

if(ph->isOOB(fhsToKeepPoints, fhsToMargPoints) || host->flaggedForMarginalization)

这里有两点，一个是该点构成的误差项较少（OOB是Out of Boundary，也就是点投影下来没有落在视场内，因此没有构成误差项），一个是该点的Host帧被标记为边缘化。
如果满足要求，对该点的所有误差项进行遍历，重新计算误差和雅克比，误差小于一定阈值的设为active。对于active的误差，进入EFResidual::fixLinearizationF，计算了该点处的误差rtz（这是一个$8\times 1$向量，表示一个小块中8个点的误差，和前面的resF一样），并将isLinearized设置为true（这样在下一次的优化阶段就能参与到accumulateLF_MT中得到HL_top），但紧接着，如果该点的idepth_hessian大于阈值，添加边缘化标签，否则直接丢弃。而被添加了边缘化标签的点之后进入EnergyFunctional::marginalizePointsF被处理，变为了对应的先验信息。
这里的先验信息其实就是重新构建了Hessian矩阵，并且这部分矩阵一旦构建，在下次优化时线性化点并不会随着迭代的进行发生变化，这就是FEJ。

4.9.2 关键帧边缘化

边缘化点后，先提取当前帧的不成熟点FullSystem::makeNewTraces，紧接着就是边缘化关键帧FullSystem::marginalizeFrame。看一下EnergyFunctional::marginalizeFrame中是如何变更Hessian矩阵的信息的。

int ndim = nFrames*8+CPARS-8;// new dimension
int odim = nFrames*8+CPARS;// old dimension

这是变更前后Hessian矩阵的维数。

int io = fh->idx*8+CPARS;	// index of frame to move to end
int ntail = 8*(nFrames-fh->idx-1);

这是要被边缘化的帧的index以及下一帧到矩阵尾部的长度。

Vec8 bTmp = bM.segment<8>(io);
VecX tailTMP = bM.tail(ntail);
bM.segment(io,ntail) = tailTMP;
bM.tail<8>() = bTmp;

MatXX HtmpCol = HM.block(0,io,odim,8);
MatXX rightColsTmp = HM.rightCols(ntail);
HM.block(0,io,odim,ntail) = rightColsTmp;
HM.rightCols(8) = HtmpCol;

MatXX HtmpRow = HM.block(io,0,8,odim);
MatXX botRowsTmp = HM.bottomRows(ntail);
HM.block(io,0,ntail,odim) = botRowsTmp;
HM.bottomRows(8) = HtmpRow;

这里交换了Hessian矩阵以及误差矩阵中的位置，把要边缘化的块移到末尾。参考公式（50）的形式，只不过现在右下角有一个$8\times 8$的Hessian块是需要边缘化的，而左上角的大块则是需要保留的。

Mat88 hpi = HMScaled.bottomRightCorner<8,8>();
hpi = 0.5f*(hpi+hpi);
hpi = hpi.inverse();
hpi = 0.5f*(hpi+hpi);

这相当于求公式（53）前面的系数。

// schur-complement!
MatXX bli = HMScaled.bottomLeftCorner(8,ndim).transpose() * hpi;
HMScaled.topLeftCorner(ndim,ndim).noalias() -= bli * HMScaled.bottomLeftCorner(8,ndim);
bMScaled.head(ndim).noalias() -= bli*bMScaled.tail<8>();

这是减掉Schur Complement（公式（53）、（54））后的结果。这样就完成了Hessian矩阵的更新。最后舍弃所有和边缘化掉的这帧产生观测值的误差项。

参考文献
[1] Engel, J., Sturm, J., & Cremers, D. (2013). Semi-dense visual odometry for a monocular camera. In Proceedings of the IEEE international conference on computer vision (pp. 1449-1456).
[2] Engel, J., Koltun, V., & Cremers, D. (2017). Direct sparse odometry. IEEE transactions on pattern analysis and machine intelligence, 40(3), 611-625.
[3] fishmarch. LSD-SLAM解读——深度滤波器[OL]. 知乎, 2018-12-12 [2019-05-31] https://zhuanlan.zhihu.com/p/47742232.
[4] JingeTU. DSO 代码框架[OL]. 博客园, 2018-01-22 [2019-05-31] https://www.cnblogs.com/JingeTU/p/8329780.html.
[5] 高翔. DSO详解[OL]. 知乎, 2017-09-17 [2019-05-31] https://zhuanlan.zhihu.com/p/29177540.
[6] JingeTU. DSO windowed optimization 代码 (1)[OL]. 博客园, 2018-01-31 [2019-06-03] https://www.cnblogs.com/JingeTU/p/8395046.html.
[7] (加) Timothy D. Barfoot著. 机器人学中的状态估计[M]. 高翔等译. 西安: 西安交通大学出版社, 2018.
[8] 白巧克力亦唯心. SLAM中的marginalization 和 Schur complement[OL]. CSDN博客, 2016-10-15 [2019-06-10] https://blog.csdn.net/heyijia0327/article/details/52822104.
[9] JingeTU. DSO windowed optimization 代码 (2)[OL]. 博客园, 2018-03-16 [2019-06-10] https://www.cnblogs.com/JingeTU/p/8586163.html.