手搓传染病模型（SEIAR-SEA-SEA-W模型（多种群多途径动态模型，MMDM））

Code_Verse

于 2025-05-16 01:30:00 发布

阅读量1k

点赞数 32

分类专栏：传染病模型，看这一个就够了！文章标签： matlab 数学建模传染病微分方程

本文链接：https://blog.csdn.net/xyhxx99499/article/details/147975887

版权

传染病模型，看这一个就够了！专栏收录该内容

23 篇文章

订阅专栏

在传染病传播的研究中，多媒介多宿主（MMDM）模型能够更细致地刻画复杂的传播机制，为防控策略提供科学依据。本文将深入探讨如图所示的 MMDM 模型，并通过 MATLAB 代码实现其动态模拟，分析不同群体在传染病传播中的行为。

一、MMDM 模型解析

图中的 MMDM 模型由一组微分方程构成，详细描述了不同群体及环境媒介的动态变化：

\(\begin{cases} \frac{dS_1}{dt} = br \cdot N - dr \cdot S_1 - \beta_1 \cdot S_1 \cdot (I_1 + \kappa \cdot A_1) - \beta_{2 - 1} \cdot S_1 \cdot A_2 - \beta_w \cdot S_1 \cdot W_{env} - \beta_{3 - 1} \cdot S_1 \cdot A_3 \\ \frac{dE_1}{dt} = \beta_1 \cdot S_1 \cdot (I_1 + \kappa \cdot A_1) + \beta_w \cdot S_1 \cdot W_{env} + \beta_{2 - 1} \cdot S_1 \cdot A_2 + \beta_{3 - 1} \cdot S_1 \cdot A_3 - dr \cdot E_1 - p \cdot \omega_1 \cdot E_1 - (1 - p) \cdot \omega_1 \cdot E_1 \\ \frac{dA_1}{dt} = p \cdot \omega_1 \cdot E_1 - dr \cdot A_1 - \gamma' \cdot A_1 \\ \frac{dI_1}{dt} = (1 - p) \cdot \omega_1 \cdot E_1 - \gamma \cdot I_1 - (dr + f) \cdot I_1 \\ \frac{dR_1}{dt} = \gamma' \cdot A_1 + \gamma \cdot I_1 - dr \cdot R_1 \\ \frac{dW_{env}}{dt} = j \cdot A_3 \\ \frac{dS_2}{dt} = - \beta_2 \cdot S_2 \cdot A_2 - \beta_{3 - 2} \cdot S_2 \cdot A_3 \\ \frac{dE_2}{dt} = \beta_2 \cdot S_2 \cdot A_2 + \beta_{3 - 2} \cdot S_2 \cdot A_3 - \omega_2 \cdot E_2 \\ \frac{dA_2}{dt} = \omega_2 \cdot E_2 \\ \frac{dS_3}{dt} = - \beta_w \cdot S_3 \cdot W_{env} - \beta_3 \cdot S_3 \cdot A_3 - \beta_{2 - 3} \cdot S_3 \cdot A_2 \\ \frac{dE_3}{dt} = \beta_3 \cdot S_3 \cdot A_3 + \beta_{2 - 3} \cdot S_3 \cdot A_2 + \beta_w \cdot S_3 \cdot W_{env} - \omega_3 \cdot E_3 \\ \frac{dA_3}{dt} = \omega_3 \cdot E_3 \end{cases}\)

易感者 \(S_1\)：\(\frac{dS_1}{dt}\) 表示其变化率，包含出生率 \(br \cdot N\)，因接触感染者 \(I_1\)、无症状感染者 \(A_1\)、媒介 \(A_2\)、环境病原体 \(W_{env}\)、另一媒介 \(A_3\) 而减少。
暴露者 \(E_1\)：\(\frac{dE_1}{dt}\) 包含感染输入（来自 \(S_1\) 的感染），以及向不同状态的转化和自然死亡。
无症状感染者 \(A_1\)：\(\frac{dA_1}{dt}\) 由暴露者转化（\(p \cdot \omega_1 \cdot E_1\)），并考虑自然死亡和康复（\(\gamma' \cdot A_1\)）。
感染者 \(I_1\)：\(\frac{dI_1}{dt}\) 由暴露者转化（\((1 - p) \cdot \omega_1 \cdot E_1\)），并考虑康复（\(\gamma \cdot I_1\)）和死亡（\((dr + f) \cdot I_1\)）。
康复者 \(R_1\)：\(\frac{dR_1}{dt}\) 汇总无症状感染者和感染者的康复，以及自然死亡。
环境病原体 \(W_{env}\)：\(\frac{dW_{env}}{dt}\) 由媒介 \(A_3\) 释放（\(j \cdot A_3\)）。
其他群体（\(S_2, E_2, A_2, S_3, E_3, A_3\)）：各自的微分方程描述了它们在不同传播途径下的动态变化。

二、MATLAB 代码实现

1. 参数设置

br = 0.00009173;  % 出生率  
dr = 0.00007523;  % 自然死亡率  
kappa = 1;         % 无症状感染相对传染系数  
p = 0.043;         % 潜伏感染的比例  
f = 0.16;          % 致死率  

% 潜伏期和感染期（单位：天）  
omega1 = 1/11;  
gamma = 1/14;  
gamma_prime = 1/14;  

% 媒介相关参数  
beta2 = 0;         % 媒介之间的传播系数  
omega2 = 1/7;  

% 宿主相关参数  
omega3 = 1/12;  
j = 10;            % 宿主向环境传播的速率  

% 环境相关  
W = 0.048;         % 环境中的媒介密度  

% 初始值设置  
S1_0 = 10000;  E1_0 = 0;  A1_0 = 0;  I1_0 = 10;  
R1_0 = 0;  W_env_0 = 0;  S2_0 = 1000;  E2_0 = 0;  
A2_0 = 1;  S3_0 = 1000;  E3_0 = 0;  A3_0 = 1;  X_0 = 0;  

Y0 = [S1_0; E1_0; A1_0; I1_0; R1_0; W_env_0; S2_0; E2_0; A2_0; S3_0; E3_0; A3_0; X_0];  

% 时间范围（单位：天）  
tspan = linspace(0, 365, 365);  

% 其他参数  
beta0 = 0.0005;  alpha = 0;  T = 365;

代码详细设置了出生率、死亡率、传播系数、潜伏期和感染期等参数，并初始化各群体数量和环境媒介密度。

2. 求解微分方程与可视化

[t, Y] = ode45(@(t,Y) MMDM_model(t, Y, beta0, alpha, T, br, dr, kappa, p, f,...  
    omega1, gamma, gamma_prime, beta2, omega2, omega3, j, W), tspan, Y0);  

% 可视化结果  
figure;  
plot(t, Y(:,1), 'DisplayName', 'S1 (Susceptible)', 'LineWidth', 2); hold on;  
plot(t, Y(:,2), 'DisplayName', 'E1 (Exposed)', 'LineWidth', 2);  
plot(t, Y(:,3), 'DisplayName', 'A1 (Asymptomatic)', 'LineWidth', 2);  
plot(t, Y(:,4), 'DisplayName', 'I1 (Infected)', 'LineWidth', 2);  
plot(t, Y(:,5), 'DisplayName', 'R1 (Removed)', 'LineWidth', 2);  
xlabel('Time (days)'); ylabel('Population');  
title('MMDM Simulation'); legend; hold off;

使用 ode45 求解微分方程组，模拟一年（365 天）内各群体的动态变化，并通过绘图直观展示结果。

三、结果分析与应用

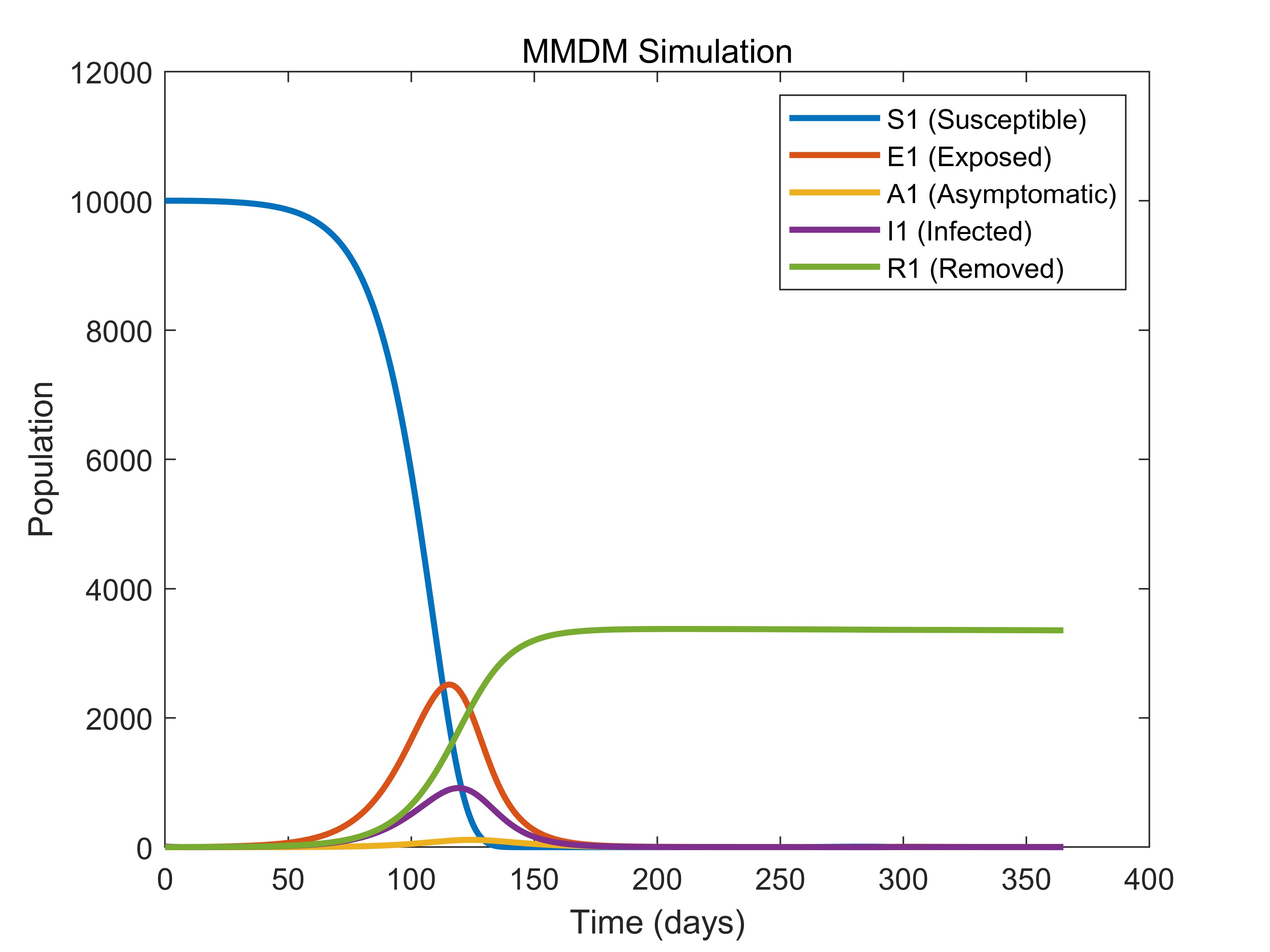
从可视化结果可以观察到：

易感者 \(S_1\)：随时间下降，因不断被感染。
暴露者 \(E_1\)：先升后降，反映感染积累与转化为其他状态的过程。
无症状感染者 \(A_1\) 和 感染者 \(I_1\)：呈现动态变化，受潜伏期和感染期参数影响。
康复者 \(R_1\)：持续增加，由感染者和无症状感染者康复而来。

MMDM 模型的应用价值在于：

防控策略评估：通过调整传播系数（如 \(\beta_1, \beta_w\)）和干预措施（如隔离、消毒），模拟不同策略对疫情的影响。
公共卫生规划：为医疗资源分配（如床位、药品）提供依据，基于模型预测不同阶段的感染人数。
研究传播机制：分析多媒介、多宿主环境下传染病的传播路径，为阻断传播提供理论支持。

四、总结

本文通过 MMDM 模型和 MATLAB 代码，实现了传染病传播的动态模拟。模型细致刻画了多群体、多媒介的复杂传播过程，代码通过参数设置、方程求解和可视化，直观展示了各群体的变化趋势。未来可进一步优化模型，纳入更多实际因素（如疫苗接种、气候影响），提升模型的实用性和准确性，为传染病防控提供更强大的支持。

通过这样的分析，我们能更好地理解传染病在多媒介多宿主环境下的传播机制，为制定精准的防控策略奠定基础，保障公众健康与安全。