用 Python 从零开始创建神经网络（十五）：Dropout

引言

另一种用于神经网络正则化的选项是添加一个dropout层。这种类型的层会禁用一些神经元，而让其他神经元保持不变。其理念与正则化类似，是为了防止神经网络对任何一个神经元的依赖过高，或在某个特定实例中完全依赖某个神经元（这在模型过拟合训练数据时很常见）。dropout还能帮助解决另一个问题，即共适应现象（co-adoption）。共适应是指神经元依赖其他神经元的输出值，而不能独立学习底层函数。通过让更多的神经元共同工作，dropout还能应对训练数据中的噪声和其他扰动，这使得模型能够学习更复杂的函数。

Dropout函数通过在每次前向传播中随机禁用一定比例的神经元来工作，这迫使网络必须学会在仅剩一部分随机选中的神经元的情况下依然进行准确的预测。Dropout强迫模型使用更多的神经元来完成相同的任务，从而提高学习描述数据底层函数的能力。例如，如果在当前步骤禁用一半的神经元，在下一步骤禁用另一半神经元，我们就强迫更多的神经元学习数据，因为只有部分神经元能够“看到”数据并在某次传播中得到更新。这种交替使用一半神经元的方式仅仅是一个例子，实际上我们会使用一个超参数来通知dropout层随机禁用的神经元数量。

此外，由于活跃的神经元是动态变化的，dropout有助于防止过拟合，因为模型不能依赖特定神经元来记住某些样本。同样需要提到的是，dropout层实际上并没有真正禁用神经元，而是将它们的输出置为零。换句话说，dropout既不会减少使用的神经元数量，也不会让训练过程在禁用一半神经元时快一倍。

1. Forward Pass

在代码中，我们将使用一个过滤器“关闭”神经元，这个过滤器是一个与层输出形状相同的数组，其中填充了从伯努利分布中抽取的数字。伯努利分布是一种二元（或离散）概率分布，其中我们可以以概率$p$获得值1，以概率$q$获得值0。让我们从这个分布中取一个随机值$r_i$，则有：

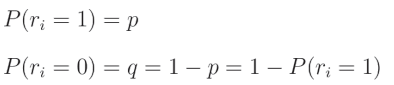
这意味着该值为1的概率是$p$，而其为0的概率是$q=1-p$，因此：

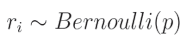
这意味着给定的$r_i$是来自伯努利分布的值，其取值为1的概率是$p$。如果$r_i$是该分布中的一个单独值，则可以从该分布中抽取一个值，并将其重新整形以匹配层输出的形状，用作这些输出的掩码。

我们得到一个数组，其中以概率$p$填充值为1，其余为0的值。然后我们将该过滤器应用于希望添加Dropout的层的输出。

代码引用：https://nnfs.io/def

在代码中，Dropout层有一个超参数。这是一个值，用于指定在该层中需要禁用的神经元的百分比。例如，如果选择了0.10作为Dropout参数，则每次前向传播中将随机禁用10%的神经元。在使用NumPy之前，我们将通过一个纯Python的示例来演示这一点（例子中演示了50%的禁用率）：

import random

dropout_rate = 0.5
# Example output containing 10 values
example_output = [0.27, -1.03, 0.67, 0.99, 0.05, -0.37, -2.01, 1.13, -0.07, 0.73]

# Repeat as long as necessary
while True:
    
    # Randomly choose index and set value to 0
    index = random.randint(0, len(example_output) - 1)
    example_output[index] = 0
    
    # We might set an index that already is zeroed
    # There are different ways of overcoming this problem,
    # for simplicity we count values that are exactly 0
    # while it's extremely rare in real model that weights
    # are exactly 0, this is not the best method for sure
    dropped_out = 0
    for value in example_output:
        if value == 0:
            dropped_out += 1
            
    # If required number of outputs is zeroed - leave the loop
    if dropped_out / len(example_output) >= dropout_rate:
        break
print(example_output)

>>>
[0, -1.03, 0.67, 0.99, 0, -0.37, 0, 0, 0, 0.73]

代码相对基础，但其思想是随机将神经元的输出置为0，直到禁用达到目标百分比的神经元。如果我们将伯努利分布视为二项分布的一个特殊情况（$n=1$），并查看NumPy中可用的方法列表，会发现使用numpy.random.binomial可以更简洁地实现这一目标。二项分布与伯努利分布的唯一区别是增加了一个参数$n$，即并发实验的次数（而不仅仅是一次实验），并返回这些$n$次实验中的成功次数。

np.random.binomial()通过接受前面讨论过的参数$n$（实验次数）和$p$（实验结果为1的概率）以及一个额外的参数size来工作：np.random.binomial(n, p, size)。

这个函数本质上可以被视为一次掷硬币实验，其中结果将是0或1。参数$n$表示你想要掷硬币的次数，$p$是掷硬币结果为1的概率。总体结果是所有掷硬币结果的总和。参数size表示要运行多少次这样的“实验”，返回的是一个总体结果的列表。例如：

import random
import numpy as np

binomial_results = np.random.binomial(2, 0.5, size=10)
print(binomial_results)

这将生成一个大小为10的数组，其中每个元素是两次掷硬币结果的总和，掷硬币结果为1的概率为0.5或50%。生成的数组如下：

>>>
[0 2 1 1 2 1 0 1 1 1]

我们可以使用上述方法创建一个Dropout层。这里的目标是创建一个滤波器，其中表示目标Dropout百分比的部分为0，其余部分为1。例如，假设我们有一个包含5个神经元的层，在其后添加一个Dropout层，并希望实现20%的Dropout率。那么，理想状态下一个Dropout层的示例如下：

[1, 0, 1, 1, 1]

如你所见，这个列表的五分之一是0。这就是我们将应用于全连接层输出的滤波器的一个示例。如果将神经网络层的输出与这个滤波器相乘，就会有效地禁用与0对应的索引处的神经元。

我们可以通过以下方式使用np.random.binomial()来模拟这一过程：

dropout_rate = 0.20
np.random.binomial(1, 1-dropout_rate, size=5)

import random
import numpy as np

dropout_rate = 0.20
binomial_results = np.random.binomial(1, 1-dropout_rate, size=5)
print(binomial_results)

>>>
[1 0 1 1 1]

这是基于概率的，因此有时生成的数组可能不会像上面的示例那样。有可能没有神经元被置零，或者所有神经元都被置零。但总体上，这些随机抽样会趋向于我们期望的概率值。此外，上述示例使用了一个非常小的层（5个神经元）。在实际规模的层中，您会发现概率更一致地匹配您设定的目标值。

假设一个神经网络层的输出是：

example_output = np.array([0.27, -1.03, 0.67, 0.99, 0.05, -0.37, -2.01, 1.13, -0.07, 0.73])

接下来，假设我们的目标Dropout率为 0.3，即 30%。我们应用Dropout层：

import random
import numpy as np

dropout_rate = 0.3
example_output = np.array([0.27, -1.03, 0.67, 0.99, 0.05, -0.37, -2.01, 1.13, -0.07, 0.73])
example_output *= np.random.binomial(1, 1-dropout_rate, example_output.shape)

print(example_output)

>>>
[ 0.27 -1.03  0.67  0.99  0.05 -0.37 -2.01  1.13 -0.    0.73]

请注意，我们的dropout率是我们计划禁用的神经元比例（$q$）。有时，dropout的实现会包含一个rate参数，它表示我们计划保留的神经元比例（$p$）。在本文写作时，深度学习框架TensorFlow和Keras中的dropout参数表示您计划禁用的神经元比例。而在PyTorch框架以及dropout的原始论文（http://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf）中，dropout参数表示您计划保留的神经元比例。

具体的实现方式并不重要，重要的是您需要清楚自己正在使用哪种方法！

尽管dropout有助于神经网络的泛化并对训练非常有益，但在进行预测时，我们并不希望使用它。这并不是仅仅省略dropout这么简单，因为下一层神经元的输入幅度可能会显著不同。例如，如果您的dropout率为50%，这意味着假设是全连接网络，下一层神经元的输入总和平均会小50%。也就是说，在训练中使用dropout时，随机的50%神经元会在每个步骤中输出0。下一层的神经元将输入乘以权重并求和，对于一半的输入接收值为0。如果我们在预测时不使用dropout，所有神经元将输出它们的值，这种状态将不匹配训练期间的状态，因为总和统计上会大约增加一倍。

为了解决这一问题，在预测期间，我们可能会将所有输出乘以dropout比例，但这会为前向传播添加额外步骤，有一种更好的方法可以实现这一点。相反，我们希望在训练阶段的dropout后，将数据重新放大，以模拟所有神经元输出其值时总和的均值。

例如，输出将变为：

import random
import numpy as np

dropout_rate = 0.3
example_output = np.array([0.27, -1.03, 0.67, 0.99, 0.05, -0.37, -2.01, 1.13, -0.07, 0.73])
example_output *= np.random.binomial(1, 1-dropout_rate, example_output.shape) / (1-dropout_rate)

print(example_output)

>>>
[ 0.38571429 -1.47142857  0.          1.41428571  0.07142857 -0.
 -0.          1.61428571 -0.          1.04285714]

请注意，我们在dropout结果中加入了除以dropout比例的操作。由于该比例是一个小数，这会使得结果值更大，从而弥补了一部分神经元输出被置零所导致的值的损失。这样，我们在预测时就不必担心这个问题，可以简单地在预测过程中省略dropout。

在任何具体示例中，您会发现缩放后的值总和与之前并不完全相等，因为我们是随机丢弃神经元。不过，经过足够多的样本后，这种缩放的效果会整体平均化。为证明这一点：

import numpy as np

dropout_rate = 0.2
example_output = np.array([0.27, -1.03, 0.67, 0.99, 0.05, -0.37, -2.01, 1.13, -0.07, 0.73])
print(f'sum initial {
     
     sum(example_output)}')

sums = []
for i in range(10000):
    example_output2 = example_output * np