机器学习实战-Logistic回归

最近在看《机器学习实战》这本书。机器学习的算法总免不了一堆数学公式的推导，看起来还是比较晦涩难懂。看看网友的文章再自己翻翻高数的书本，尝试自己推导下，总算有点明白了，写下来再加深下理解。

Logistic回归属于优化类的算法。Logistic回归的主要思想：根据现有的数据对分类边界线建立回归公式，达到分类的目的。假设我们有一堆数据，需要划一条线(最佳直线)对其分类，这就是Logistic回归的目的了。

1.Sigmoid函数

在了解Logistic回归之前，需要知道下这个神奇的函数。
具体计算公式如下：

$$\sigma(z)=\frac{1}{1+e^{-z}}$$

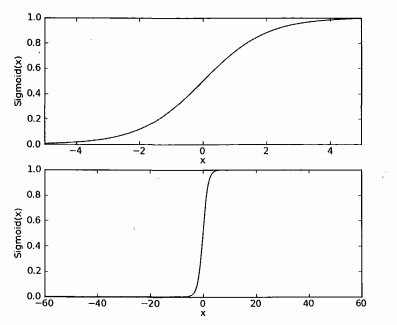
附上书上的曲线图：

从图中可以看出该函数的效果可以把x轴上无限大的数值映射到(0,1)之间。这和概率事件中，事件发生的概率值区域很相似。
为了实现回归分类器模型，可以在每个特征上都乘以一个回归系数，然后进行累加，再输入到sigmoid函数，得到(0,1)之间的一个值，以0.5为分界线，结果大于0.5的可以归为1类，否则归为0类。

这里的回归系数就是我们要求解的值。

2.最佳回归系数的确定

对于Sigmoid函数输入$z=w_0x_0+w_0x_0+...+w_nx_n$
x写成向量的形式，我们记为：$z=w^Tx$。
这里的x表示多个特征，w表示相应的权重(个人理解)。

举个栗子：甩给你100个手机，其中有30个是你喜欢的，70个是不喜欢的。为了预测你对第101个手机的喜好。首先，对手机取特征，比如，价格，外观，用户体验；简单处理，只考虑3个方面(即3个特征)。也就是公式中的n个x。那么w就是相应权重，权重越高也就表示你最看重哪方面。
如果我们知道这个权重值，然后只要把第101只手机的参数(假设3个方面都有一个客观的评分值0-10)代入公式就能得到z的值 如果z的值越高，说明你喜欢的可能性越高。

这一切的前提是我们能得到权重(即w)。
以上栗子可能不是十分恰当，不过大概就是这么个意思。。。。-.-

2.1开始公式推导

这里我们令$h_z(x)=g(w^Tx)=\frac{1}{1+e^{-w^Tx}}$

对于x的属于1类或者是0类的条件概率我们可以写成：

$p(y=1|x,w)=h_z(x)$
$p(y=0|x,w)=1-h_z(x)$

把这个表达式进行合并，得到：

$p(y|x,w)=h_z(x)^y(1-h_z(x))^{1-y}$

到了这里，我们还是不知道这个w该如何得到。
这里还要引入一个最大似然估计的概念。
最大似然估计的含义：我们现在有m个样本，那么可以估计存在某个参数使得这组样本出现的可能性最大。
现在这个样本出现的概率：

$L(w)=\Pi_{i=1}^np(y^i|x,w)=\Pi_{i=1}^nh_z(x^i)^{y^i}(1-h_z(x^i))^{1-y}$

其中m=样本总数，$x^i$表示第i个样本，$y^i$表示其类别
为了让上式最大似然估计函数得到最大值。
那么我们可以对其求导。但是这个函数很复杂，直接求导比较麻烦。这里先转化为对数函数。(转化为对数，不影响原来函数的变化趋势，即原来是递增转化之后依然是递增)。
$l(w)=y^ilogh_z(x^i)+(1-y)log(1-h_z(x^i))$

2.2梯度上升算法

上面的函数依然比较复杂。如果只是简单的2次方程：
$f(x)=-x^2+2x+1$
对其求导就是$f'(x)=-2x+2$
假设如图：

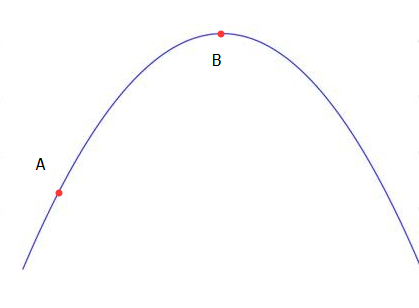
那么我们就能知道x=1时有最大值。但上面这个函数很复杂，没这么简单可以求得。
以上图为例，如果不能直接以求导得到极值，那么可以选择爬坡来实现。
随机选择A点，要得到B点的极值。那么可以慢慢往上爬。
这里是往上爬还是往下爬呢？我们可以这样来确定。

$$x_{i+1}=x_i+\alpha\frac{\partial(x_i)}{x_i}$$
这里的 $\alpha$表示步长，每次爬多远，通常是很小的值比如0.01，后面的则是该点对x求偏导，也就是爬的方向，以A点为例，其偏导>0，即不断往上爬，当接近B点的时候x的值会趋于稳定，就可以结束爬坡了。这个过程需要迭代很多次，通常计算机会干这个活。
那么我们刚才这个函数比较复杂也可以通过爬坡来实现，只要我们得到这个偏导。
求偏导：

$\frac{\partial l(w)}{\partial w_j}=\frac{\partial l(w)}{\partial g(w^Tx)}*\frac{\partial g(w^Tx)}{\partial w^Tx}*\frac{\partial w^Tx}{\partial w_j}$

其中：

1.$\frac{\partial l(w)}{\partial g(w^Tx)}=y*\frac{1}{g(wTx)}+(1-y)\frac{1}{1-g(w^Tx)}(-1)$
2.$\frac{\partial g(w^Tx)}{\partial w^Tx}=(-1)(1+e^{w^Tx})^{-2}e^{-w^Tx}(-1)=g(w^Tx)\frac{e^{-w^Tx}}{1+e^{w^Tx}}=g(w^Tx)(1-g(w^Tx))$
3.$\frac{\partial w^Tx}{\partial w_j}=\frac{\partial (w_0x0+w_1x_1+...+w_mx_m)}{\partial w_j}=x_j$

由1.2.3.可得

$\frac{\partial l(w)}{\partial w_j}=y*\frac{1}{g(wTx)}+(1-y)\frac{1}{1-g(w^Tx)}(-1)g(w^Tx)(1-g(w^Tx))x_j=(y(1-g(w^Tx))-(1-y)g(w^Tx))x_j=(y-g(w^Tx))x_j$

因此梯度迭代公式：
$w_j=w_j+\alpha(y-h_w(x^i))x_j^i$
这里的$w_j$表示$x_j$对应的权重系数。

3.code

再回头看看书上的代码：

def calcgrand(dataMatin,labelMatin,cyc_num=500):
    dataMat=mat(dataMatin)
    labelMat=mat(labelMatin).transpose()
    n=shape(dataMat)[1]
    weight=ones((n,1))
    alpha=0.001
    for i in range(cyc_num):
        h=sigmod(dataMat*weight)
        weight=weight+alpha*dataMat.transpose()*(labelMat-h)
    return weight

这里的labelMat-h相当于$y-h_w(x)$这里是整个向量代入计算，书中后面的优化部分则是labelMat[i]-h相当于$y-h_w(x^i)$.
推导结束，算是知道了代码中的计算公式哪里来的。
附上最后的随机梯度算法代码&效果图：

def stocalcgrand1(dataMatin,labelMatin,numiter=150):
    m,n=shape(dataMatin)
    alpha=0.01
    weight=ones(n)
    for i in range(numiter):
        dataIndex=range(m)
        for j in range(m):
            alpha=4/(1.0+j+i)+0.01
            randIndex=int(random.uniform(0,len(dataIndex)))
            h=sigmod(sum(dataMatin[dataIndex[randIndex]]*weight))
            error=labelMatin[dataIndex[randIndex]]-h
            weight=weight+alpha*error*dataMatin[dataIndex[randIndex]]
            del(dataIndex[randIndex])
    return weight

代码和书上的略有不同。
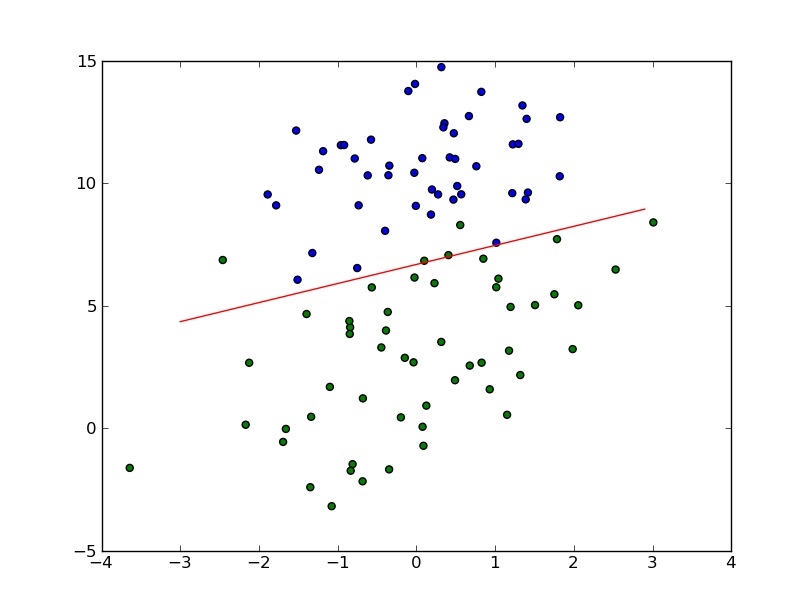
效果图:

4.end

---

参考：

[1]:http://sbp810050504.blog.51cto.com/2799422/1608064
[2]:http://cs229.stanford.edu/notes/cs229-notes1.pdf