6 逻辑回归(Logistic Regression)
6.1 分类(Classification)
在分类问题中,预测的结果是离散值(结果是否属于某一类),逻辑回归算法(Logistic Regression)被用于解决这类分类问题。
- 垃圾邮件判断
- 金融欺诈判断
- 肿瘤诊断
讨论肿瘤诊断问题:
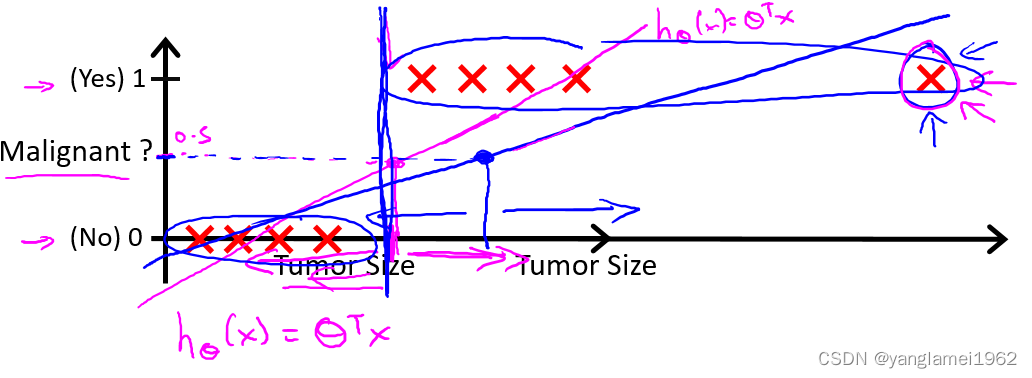
肿瘤诊断问题的目的是告诉病人是否为恶性肿瘤,是一个二元分类问题(binary class problems),则定义 $ y \in\lbrace 0, 1\rbrace$,其中 0 表示负向类(negative class),代表恶性肿瘤(“-”),1 为正向类(positive class),代表良性肿瘤(“+”)。如图,定义最右边的样本为偏差项。
在未加入偏差项时,线性回归算法给出了品红色的拟合直线,若规定
h θ ( x ) ⩾ 0.5 h_\theta(x) \geqslant 0.5 hθ(x)⩾0.5 ,预测为 y = 1 y = 1 y=1,即正向类;
h θ ( x ) < 0.5 h_\theta(x) \lt 0.5 hθ(x)<0.5 ,预测为 y = 0 y = 0 y=0,即负向类。
即以 0.5 为阈值(threshold),则我们就可以根据线性回归结果,得到相对正确的分类结果 y y y。
接下来加入偏差项,线性回归算法给出了靛青色的拟合直线,如果阈值仍然为 0.5,可以看到算法在某些情况下会给出完全错误的结果,对于癌症、肿瘤诊断这类要求预测极其精确的问题,这种情况是无法容忍的。
不仅如此,线性回归算法的值域为全体实数集( h θ ( x ) ∈ R h_\theta(x) \in R hθ(x)∈R),则当线性回归函数给出诸如 h θ ( x ) = 10000 , h θ ( x ) = − 10000 h_\theta(x) = 10000, h_\theta(x) = -10000 hθ(x)=10000,hθ(x)=−10000 等很大/很小(负数)的数值时,结果 y ∈ { 0 , 1 } y \in \lbrace 0, 1\rbrace y∈{0,1},这显得非常怪异。
区别于线性回归算法,逻辑回归算法是一个分类算法,其输出值永远在 0 到 1 之间,即 h θ ( x ) ∈ ( 0 , 1 ) h_\theta(x) \in (0,1) hθ(x)∈(0,1)。
6.2 假设函数表示(Hypothesis Representation
为了使
h
θ
(
x
)
∈
(
0
,
1
)
h_\theta(x) \in \left(0, 1\right)
hθ(x)∈(0,1),引入逻辑回归模型,定义假设函数
h
θ
(
x
)
=
g
(
z
)
=
g
(
θ
T
x
)
h_\theta \left( x \right)=g(z)=g\left(\theta^{T}x \right)
hθ(x)=g(z)=g(θTx)
对比线性回归函数
h
θ
(
x
)
=
θ
T
x
h_\theta \left( x \right)=\theta^{T}x
hθ(x)=θTx,
g
g
g 表示逻辑函数(logistic function),复合起来,则称为逻辑回归函数。
逻辑函数是 S 形函数,会将所有实数映射到 ( 0 , 1 ) (0, 1) (0,1) 范围。
sigmoid 函数(如下图)是逻辑函数的特殊情况,其公式为 g ( z ) = 1 1 + e − z g\left( z \right)=\frac{1}{1+{{e}^{-z}}} g(z)=1+e−z1。

应用 sigmoid 函数,则逻辑回归模型: h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x h_{\theta}(x)=g(\theta^Tx) =\frac{1}{1+e^{-\theta^Tx}} hθ(x)=g(θTx)=1+e−θTx1
逻辑回归模型中, h θ ( x ) h_\theta \left( x \right) hθ(x) 的作用是,根据输入 x x x 以及参数 θ \theta θ,计算得出”输出 y = 1 y=1 y=1“的可能性(estimated probability),概率学中表示为:
h
θ
(
x
)
=
P
(
y
=
1
∣
x
;
θ
)
=
1
−
P
(
y
=
0
∣
x
;
θ
)
P
(
y
=
0
∣
x
;
θ
)
+
P
(
y
=
1
∣
x
;
θ
)
=
1
\begin{align*} & h_\theta(x) = P(y=1 | x ; \theta) = 1 - P(y=0 | x ; \theta) \\ & P(y = 0 | x;\theta) + P(y = 1 | x ; \theta) = 1 \end{align*}
hθ(x)=P(y=1∣x;θ)=1−P(y=0∣x;θ)P(y=0∣x;θ)+P(y=1∣x;θ)=1
以肿瘤诊断为例,
h
θ
(
x
)
=
0.7
h_\theta \left( x \right)=0.7
hθ(x)=0.7 表示病人有
70
%
70\%
70% 的概率得了恶性肿瘤。
6.3 决策边界(Decision Boundary)
决策边界的概念,可帮助我们更好地理解逻辑回归模型的拟合原理。
在逻辑回归中,有假设函数 h θ ( x ) = g ( z ) = g ( θ T x ) h_\theta \left( x \right)=g(z)=g\left(\theta^{T}x \right) hθ(x)=g(z)=g(θTx)。
为了得出分类的结果,这里和前面一样,规定以 0.5 0.5 0.5 为阈值:
h
θ
(
x
)
≥
0.5
→
y
=
1
h
θ
(
x
)
<
0.5
→
y
=
0
\begin{align*} & h_\theta(x) \geq 0.5 \rightarrow y = 1 \\ & h_\theta(x) < 0.5 \rightarrow y = 0 \\ \end{align*}
hθ(x)≥0.5→y=1hθ(x)<0.5→y=0
回忆一下 sigmoid 函数的图像:

观察可得当 g ( z ) ≥ 0.5 g(z) \geq 0.5 g(z)≥0.5 时,有 z ≥ 0 z \geq 0 z≥0,即 θ T x ≥ 0 \theta^Tx \geq 0 θTx≥0。
同线性回归模型的不同点在于:
z
→
+
∞
,
e
−
∞
→
0
⇒
g
(
z
)
=
1
z
→
−
∞
,
e
∞
→
∞
⇒
g
(
z
)
=
0
\begin{align*} z \to +\infty, e^{-\infty} \to 0 \Rightarrow g(z)=1 \\ z \to -\infty, e^{\infty}\to \infty \Rightarrow g(z)=0 \end{align*}
z→+∞,e−∞→0⇒g(z)=1z→−∞,e∞→∞⇒g(z)=0
直观一点来个例子,
h
θ
(
x
)
=
g
(
θ
0
+
θ
1
x
1
+
θ
2
x
2
)
{h_\theta}\left( x \right)=g\left( {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}\right)
hθ(x)=g(θ0+θ1x1+θ2x2) 是下图模型的假设函数:
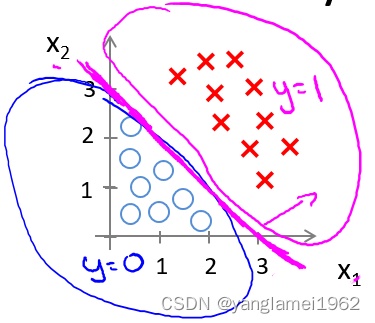
根据上面的讨论,要进行分类,那么只要 $ {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}\geq0$ 时,就预测 y = 1 y = 1 y=1,即预测为正向类。
如果取 θ = [ − 3 1 1 ] \theta = \begin{bmatrix} -3\\1\\1\end{bmatrix} θ= −311 ,则有 z = − 3 + x 1 + x 2 z = -3+{x_1}+{x_2} z=−3+x1+x2,当 z ≥ 0 z \geq 0 z≥0 即 x 1 + x 2 ≥ 3 {x_1}+{x_2} \geq 3 x1+x2≥3 时,易绘制图中的品红色直线即决策边界,为正向类(以红叉标注的数据)给出 y = 1 y=1 y=1 的分类预测结果。
上面讨论了逻辑回归模型中线性拟合的例子,下面则是一个多项式拟合的例子,和线性回归中的情况也是类似的。
为了拟合下图数据,建模多项式假设函数:
h
θ
(
x
)
=
g
(
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
1
2
+
θ
4
x
2
2
)
{h_\theta}\left( x \right)=g\left( {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}+{\theta_{3}}x_{1}^{2}+{\theta_{4}}x_{2}^{2} \right)
hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22)
这里取
θ
=
[
−
1
0
0
1
1
]
\theta = \begin{bmatrix} -1\\0\\0\\1\\1\end{bmatrix}
θ=
−10011
,决策边界对应了一个在原点处的单位圆(
x
1
2
+
x
2
2
=
1
{x_1}^2+{x_2}^2 = 1
x12+x22=1),如此便可给出分类结果,如图中品红色曲线:
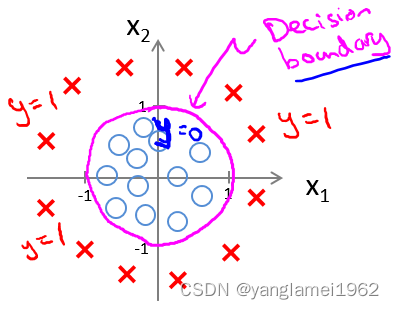
当然,通过一些更为复杂的多项式,还能拟合那些图像显得非常怪异的数据,使得决策边界形似碗状、爱心状等等。
简单来说,决策边界就是分类的分界线,分类现在实际就由 z z z (中的 θ \theta θ)决定啦。
6.4 代价函数(Cost Function)
那我们怎么知道决策边界是啥样? θ \theta θ 多少时能很好的拟合数据?当然,见招拆招,总要来个 J ( θ ) J(\theta) J(θ)。
如果直接套用线性回归的代价函数: J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( {\theta} \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( h_{\theta} \left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
其中 h θ ( x ) = g ( θ T x ) h_\theta(x) = g\left(\theta^{T}x \right) hθ(x)=g(θTx),可绘制关于 J ( θ ) J(\theta) J(θ) 的图像,如下图
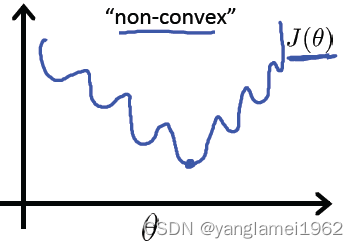
回忆线性回归中的平方损失函数,其是一个二次凸函数(碗状),二次凸函数的重要性质是只有一个局部最小点即全局最小点。上图中有许多局部最小点,这样将使得梯度下降算法无法确定收敛点是全局最优。
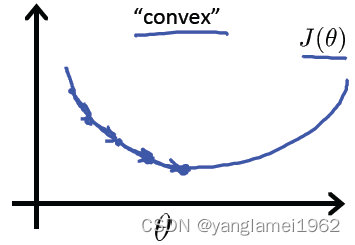
如果此处的损失函数也是一个凸函数,是否也有同样的性质,从而最优化?这类讨论凸函数最优值的问题,被称为凸优化问题(Convex optimization)。
当然,损失函数不止平方损失函数一种。
对于逻辑回归,更换平方损失函数为对数损失函数,可由统计学中的最大似然估计方法推出代价函数 J ( θ ) J(\theta) J(θ):
J
(
θ
)
=
1
m
∑
i
=
1
m
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
(
i
)
)
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
log
(
h
θ
(
x
)
)
if y = 1
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
log
(
1
−
h
θ
(
x
)
)
if y = 0
\begin{align*} & J(\theta) = \dfrac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)}) \\ & \mathrm{Cost}(h_\theta(x),y) = -\log(h_\theta(x)) \; & \text{if y = 1} \\ & \mathrm{Cost}(h_\theta(x),y) = -\log(1-h_\theta(x)) \; & \text{if y = 0} \end{align*}
J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))Cost(hθ(x),y)=−log(hθ(x))Cost(hθ(x),y)=−log(1−hθ(x))if y = 1if y = 0
则有关于
J
(
θ
)
J(\theta)
J(θ) 的图像如下:
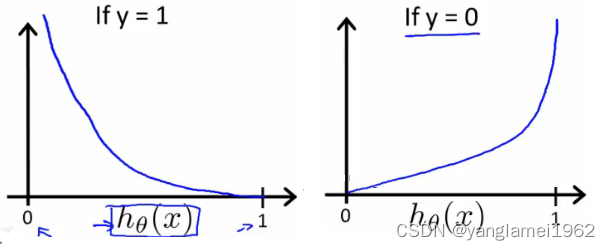
如左图,当训练集的结果为 y = 1 y=1 y=1(正样本)时,随着假设函数趋向于 1 1 1,代价函数的值会趋于 0 0 0,即意味着拟合程度很好。如果假设函数此时趋于 0 0 0,则会给出一个很高的代价,拟合程度差,算法会根据其迅速纠正 θ \theta θ 值,右图 y = 0 y=0 y=0 同理。
区别于平方损失函数,对数损失函数也是一个凸函数,但没有局部最优值。
6.5 简化的成本函数和梯度下降(Simplified Cost Function and Gradient Descent)
由于懒得分类讨论,对于二元分类问题,我们可把代价函数简化为一个函数:
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
×
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
×
l
o
g
(
1
−
h
θ
(
x
)
)
Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right)
Cost(hθ(x),y)=−y×log(hθ(x))−(1−y)×log(1−hθ(x))
当 y = 0 y = 0 y=0,左边式子整体为 0 0 0,当 y = 1 y = 1 y=1,则 1 − y = 0 1-y=0 1−y=0,右边式子整体为0,也就和上面的分段函数一样了,而一个式子计算起来更方便。
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
向量化实现:
h = g ( X θ ) h = g(X\theta) h=g(Xθ), J ( θ ) = 1 m ⋅ ( − y T log ( h ) − ( 1 − y ) T log ( 1 − h ) ) J(\theta) = \frac{1}{m} \cdot \left(-y^{T}\log(h)-(1-y)^{T}\log(1-h)\right) J(θ)=m1⋅(−yTlog(h)−(1−y)Tlog(1−h))
为了最优化 θ \theta θ,仍使用梯度下降法,算法同线性回归中一致:
Repeat until convergence: { θ j : = θ j − α ∂ ∂ θ j J ( θ ) } \begin{align*} & \text{Repeat until convergence:} \; \lbrace \\ &{{\theta }_{j}}:={{\theta }_{j}}-\alpha \frac{\partial }{\partial {{\theta }_{j}}}J\left( {\theta} \right) \\ \rbrace \end{align*} }Repeat until convergence:{θj:=θj−α∂θj∂J(θ)
解出偏导得:
Repeat until convergence: { θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) for j := 0,1...n } \begin{align*} & \text{Repeat until convergence:} \; \lbrace \\ & \theta_j := \theta_j - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \; & \text{for j := 0,1...n}\\ \rbrace \end{align*} }Repeat until convergence:{θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))⋅xj(i)for j := 0,1...n
注意,虽然形式上梯度下降算法同线性回归一样,但其中的假设函不同,即 h θ ( x ) = g ( θ T x ) h_\theta(x) = g\left(\theta^{T}x \right) hθ(x)=g(θTx),不过求导后的结果也相同。
向量化实现: θ : = θ − α m X T ( g ( X θ ) − y ) \theta := \theta - \frac{\alpha}{m} X^{T} (g(X \theta ) - y) θ:=θ−mαXT(g(Xθ)−y)
逻辑回归中代价函数求导的推导过程:
J
(
θ
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
log
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
h
θ
(
x
(
i
)
)
)
]
J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))]
J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
令
f
(
θ
)
=
y
(
i
)
log
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
h
θ
(
x
(
i
)
)
)
f(\theta) = {{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)
f(θ)=y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))
忆及 h θ ( x ) = g ( z ) h_\theta(x) = g(z) hθ(x)=g(z), g ( z ) = 1 1 + e ( − z ) g(z) = \frac{1}{1+e^{(-z)}} g(z)=1+e(−z)1,则
f ( θ ) = y ( i ) log ( 1 1 + e − z ) + ( 1 − y ( i ) ) log ( 1 − 1 1 + e − z ) = − y ( i ) log ( 1 + e − z ) − ( 1 − y ( i ) ) log ( 1 + e z ) \begin{align*} f(\theta) &= {{y}^{(i)}}\log \left( \frac{1}{1+{{e}^{-z}}} \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-\frac{1}{1+{{e}^{-z}}} \right) \\ &= -{{y}^{(i)}}\log \left( 1+{{e}^{-z}} \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1+{{e}^{z}} \right) \end{align*} f(θ)=y(i)log(1+e−z1)+(1−y(i))log(1−1+e−z1)=−y(i)log(1+e−z)−(1−y(i))log(1+ez)
忆及 z = θ T x ( i ) z=\theta^Tx^{(i)} z=θTx(i),对 θ j \theta_j θj 求偏导,则没有 θ j \theta_j θj 的项求偏导即为 0 0 0,都消去,则得:
∂
z
∂
θ
j
=
∂
∂
θ
j
(
θ
T
x
(
i
)
)
=
x
j
(
i
)
\frac{\partial z}{\partial {\theta_{j}}}=\frac{\partial }{\partial {\theta_{j}}}\left( \theta^Tx^{(i)} \right)=x^{(i)}_j
∂θj∂z=∂θj∂(θTx(i))=xj(i)
所以有:
∂ ∂ θ j f ( θ ) = ∂ ∂ θ j [ − y ( i ) log ( 1 + e − z ) − ( 1 − y ( i ) ) log ( 1 + e z ) ] = − y ( i ) ∂ ∂ θ j ( − z ) e − z 1 + e − z − ( 1 − y ( i ) ) ∂ ∂ θ j ( z ) e z 1 + e z = − y ( i ) − x j ( i ) e − z 1 + e − z − ( 1 − y ( i ) ) x j ( i ) 1 + e − z = ( y ( i ) e − z 1 + e − z − ( 1 − y ( i ) ) 1 1 + e − z ) x j ( i ) = ( y ( i ) e − z 1 + e − z − ( 1 − y ( i ) ) 1 1 + e − z ) x j ( i ) = ( y ( i ) ( e − z + 1 ) − 1 1 + e − z ) x j ( i ) = ( y ( i ) − 1 1 + e − z ) x j ( i ) = ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) = − ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \begin{align*} \frac{\partial }{\partial {\theta_{j}}}f\left( \theta \right)&=\frac{\partial }{\partial {\theta_{j}}}[-{{y}^{(i)}}\log \left( 1+{{e}^{-z}} \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1+{{e}^{z}} \right)] \\ &=-{{y}^{(i)}}\frac{\frac{\partial }{\partial {\theta_{j}}}\left(-z \right) e^{-z}}{1+e^{-z}}-\left( 1-{{y}^{(i)}} \right)\frac{\frac{\partial }{\partial {\theta_{j}}}\left(z \right){e^{z}}}{1+e^{z}} \\ &=-{{y}^{(i)}}\frac{-x^{(i)}_je^{-z}}{1+e^{-z}}-\left( 1-{{y}^{(i)}} \right)\frac{x^{(i)}_j}{1+e^{-z}} \\ &=\left({{y}^{(i)}}\frac{e^{-z}}{1+e^{-z}}-\left( 1-{{y}^{(i)}} \right)\frac{1}{1+e^{-z}}\right)x^{(i)}_j \\ &=\left({{y}^{(i)}}\frac{e^{-z}}{1+e^{-z}}-\left( 1-{{y}^{(i)}} \right)\frac{1}{1+e^{-z}}\right)x^{(i)}_j \\ &=\left(\frac{{{y}^{(i)}}(e^{-z}+1)-1}{1+e^{-z}}\right)x^{(i)}_j \\ &={({{y}^{(i)}}-\frac{1}{1+{{e}^{-z}}})x_j^{(i)}} \\ &={\left({{y}^{(i)}}-{h_\theta}\left( {{x}^{(i)}} \right)\right)x_j^{(i)}} \\ &=-{\left({h_\theta}\left( {{x}^{(i)}} \right)-{{y}^{(i)}}\right)x_j^{(i)}} \end{align*} ∂θj∂f(θ)=∂θj∂[−y(i)log(1+e−z)−(1−y(i))log(1+ez)]=−y(i)1+e−z∂θj∂(−z)e−z−(1−y(i))1+ez∂θj∂(z)ez=−y(i)1+e−z−xj(i)e−z−(1−y(i))1+e−zxj(i)=(y(i)1+e−ze−z−(1−y(i))1+e−z1)xj(i)=(y(i)1+e−ze−z−(1−y(i))1+e−z1)xj(i)=(1+e−zy(i)(e−z+1)−1)xj(i)=(y(i)−1+e−z1)xj(i)=(y(i)−hθ(x(i)))xj(i)=−(hθ(x(i))−y(i))xj(i)
则可得代价函数的导数:
∂ ∂ θ j J ( θ ) = − 1 m ∑ i = 1 m ∂ ∂ θ j f ( θ ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) \frac{\partial }{\partial {\theta_{j}}}J(\theta) = -\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{\partial }{\partial {\theta_{j}}}f(\theta)}=\frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} ∂θj∂J(θ)=−m1i=1∑m∂θj∂f(θ)=m1i=1∑m(hθ(x(i))−y(i))⋅xj(i)
6.6 进阶优化(Advanced Optimization)
运行梯度下降算法,其能最小化代价函数 J ( θ ) J(\theta) J(θ) 并得出 θ \theta θ 的最优值,在使用梯度下降算法时,如果不需要观察代价函数的收敛情况,则直接计算 J ( θ ) J(\theta) J(θ) 的导数项即可,而不需要计算 J ( θ ) J(\theta) J(θ) 值。
我们编写代码给出代价函数及其偏导数然后传入梯度下降算法中,接下来算法则会为我们最小化代价函数给出参数的最优解。这类算法被称为最优化算法(Optimization Algorithms),梯度下降算法不是唯一的最小化算法[^1]。
一些最优化算法:
- 梯度下降法(Gradient Descent)
- 共轭梯度算法(Conjugate gradient)
- 牛顿法和拟牛顿法(Newton’s method & Quasi-Newton Methods)
- DFP算法
- 局部优化法(BFGS)
- 有限内存局部优化法(L-BFGS)
- 拉格朗日乘数法(Lagrange multiplier)
比较梯度下降算法:一些最优化算法虽然会更为复杂,难以调试,自行实现又困难重重,开源库又效率也不一,哎,做个调包侠还得碰运气。不过这些算法通常效率更高,并无需选择学习速率 α \alpha α(少一个参数少一份痛苦啊!)。
Octave/Matlab 中对这类高级算法做了封装,易于调用。
假设有 J ( θ ) = ( θ 1 − 5 ) 2 + ( θ 2 − 5 ) 2 J(\theta) = (\theta_1-5)^2 + (\theta_2-5)^2 J(θ)=(θ1−5)2+(θ2−5)2,要求参数 θ = [ θ 1 θ 2 ] \theta=\begin{bmatrix} \theta_1\\\theta_2\end{bmatrix} θ=[θ1θ2]的最优值。
下面为 Octave/Matlab 求解最优化问题的代码实例:
- 创建一个函数以返回代价函数及其偏导数:
function [jVal, gradient] = costFunction(theta)
% code to compute J(theta)
jVal=(theta(1)-5)^2+(theta(2)-5)^2;
% code to compute derivative of J(theta)
gradient=zeros(2,1);
gradient(1)=2*(theta(1)-5);
gradient(2)=2*(theta(2)-5);
end
- 将
costFunction函数及所需参数传入最优化函数fminunc,以求解最优化问题:
options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);
'GradObj', 'on': 启用梯度目标参数(则需要将梯度传入算法)
'MaxIter', 100: 最大迭代次数为 100 次
@xxx: Octave/Matlab 中的函数指针
optTheta: 最优化得到的参数向量
functionVal: 引用函数最后一次的返回值
exitFlag: 标记代价函数是否收敛
注:Octave/Matlab 中可以使用 help fminunc 命令随时查看函数的帮助文档。
- 返回结果
optTheta =
5
5
functionVal = 0
exitFlag = 1
6.7 多类别分类: 一对多(Multiclass Classification: One-vs-all)
一直在讨论二元分类问题,这里谈谈多类别分类问题(比如天气预报)。
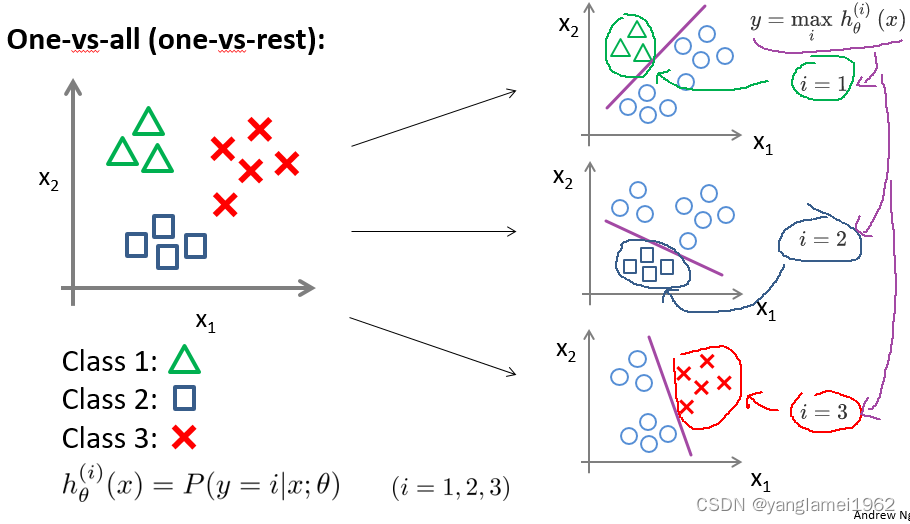
原理是,转化多类别分类问题为多个二元分类问题,这种方法被称为 One-vs-all。
正式定义: h θ ( i ) ( x ) = p ( y = i ∣ x ; θ ) , i = ( 1 , 2 , 3.... k ) h_\theta^{\left( i \right)}\left( x \right)=p\left( y=i|x;\theta \right), i=\left( 1,2,3....k \right) hθ(i)(x)=p(y=i∣x;θ),i=(1,2,3....k)
h θ ( i ) ( x ) h_\theta^{\left( i \right)}\left( x \right) hθ(i)(x): 输出 y = i y=i y=i(属于第 i i i 个分类)的可能性
k k k: 类别总数,如上图 k = 3 k=3 k=3。
注意多类别分类问题中 h θ ( x ) h_\theta(x) hθ(x) 的结果不再只是一个实数而是一个向量,如果类别总数为 k k k,现在 h θ ( x ) h_\theta(x) hθ(x) 就是一个 k k k 维向量。
对于某个样本实例,需计算所有的 k k k 种分类情况得到 h θ ( x ) h_\theta(x) hθ(x),然后看分为哪个类别时预测输出的值最大,就说它输出属于哪个类别,即 y = max i h θ ( i ) ( x ) y = \mathop{\max}\limits_i\,h_\theta^{\left( i \right)}\left( x \right) y=imaxhθ(i)(x)。






















 478
478











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










