数学期望相关（有新发现会补充）

广义定义：一次随机抽样中所期望的某随机变量的取值。

数学定义：

1.离散型

设离散型随机变量X的分布为 若级数 则记。E(X)为随机变量的数学期望。

小于正无穷时为了保证与求和次序无关，若等于正无穷，则期望不存在。

2.连续型

设X为连续的随机变量，其分布函数为F(x)，若，记，称E(X)为随机变量X的数学期望。

分布函数（英文Cumulative Distribution Function, 简称CDF），是概率统计中重要的函数，正是通过它，可用数学分析的方法来研究随机变量。 分布函数是随机变量最重要的概率特征，分布函数可以完整地描述随机变量的统计规律，并且决定随机变量的一切其他概率特征。概率分布函数和概率密度函数，我认为的分布函数就是离散的概率函数，对于每个x都有相对应的概率值。而概率密度函数就是连续的概率值函数。  

期望值像是随机试验在同样的机会下重复多次，所有那些可能状态平均的结果，便基本上等同“期望值”所期望的数。需要注意的是，期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。（换句话说，期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。）

例如，掷一枚公平的六面骰子，其每次“点数”的期望值是3.5，计算如下：

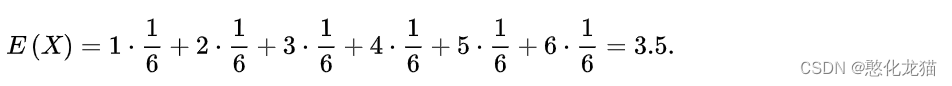
不过如上所说明的，3.5虽是“点数”的期望值，但却不属于可能结果中的任一个，没有可能掷出此点数。

期望值并不等同于均值，但将多个均值多次求均值就会无限接近期望。