算法导论 — 4.5 用主方法求解递归式

笔记

利用主定理可以对形如$T(n)=aT(n/b)+f(n)$的递归式直接求解。下面先给出主定理的描述。
　　令$a\ge 1$和$b>1$是常数，$f(n)$是一个函数，$T(n)$是定义在非负整数上的递归式：
　　　　　　$T(n)=aT(n/b)+f(n)$
　　其中我们将$n/b$解释为$\lfloor n/b\rfloor$或$\lceil n/b\rceil$。那么$T(n)$有如下渐近界：
　　•　若对某个常数$\epsilon >0$有$f(n)=O(n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a-\epsilon })$，则$T(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a})$。
　　•　若$f(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a})$，则$T(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}\mathrm{l}\mathrm{g}n)$。
　　•　若对某个常数$\epsilon >0$有$f(n)=\Omega (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a+\epsilon })$，且对某个常数$c<1$和所有足够大的$n$有$af(n/b)\le cf(n)$，则$T(n)=\Theta (f(n))$。
　　直观上来看，主定理是将函数$f(n)$与$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}$进行比较。若$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}$渐近更大，则为情况1，解为$T(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a})$；若$f(n)$渐近更大，则有可能为情况3，解为$T(n)=\Theta (f(n))$；若$f(n)$与$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}$渐近相等，则为情况2，解为$T(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}\mathrm{l}\mathrm{g}n)$。
　　需要注意的是，这里讲的“渐近大于或渐近小于”指的是“多项式意义上的渐近大于或渐近小于”。对于况1，并不是满足$f(n)$渐近小于$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}$就够了，而是在“渐近小于”的基础上还要相差一个因子$n^{\epsilon }$，即$f(n)=O(n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a-\epsilon })$，其中$\epsilon$是一个大于$0$的常数。而在第3种情况中，也并不是满足$f(n)$渐近大于$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}$就够了，而是在“渐近大于”的基础上还要相差一个因子$n^{\epsilon }$，即$f(n)=\Omega (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a+\epsilon })$。
　　另外要注意的是，主定理的3种情况并未覆盖$f(n)$的所有可能性。存在一些函数$f(n)$并不属于3种情况中的任何一种，这时就不能应用主方法来求解递归式。
　　下面通过例子来说明主方法的应用。
　　先看递归式$T(n)=9T(n/3)+n$。套用主定理，有$a=9,b=3$并且$f(n)=n$，于是有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{3}9}=n^2$。由于$f(n)=O(n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a-\epsilon })$，其中$\epsilon =1$，所以可以应用主定理的情况1，从而得到解$T(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a})=\Theta (n^2)$。
　　再看一个递归式$T(n)=T(2n/3)+1$。套用主定理，有$a=1,b=3/2$并且$f(n)=1$，于是有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{3/2}1}=n^0=1$。由于$f(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a})=\Theta (1)$，所以可以应用主定理的情况2，从而得到解$T(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}\mathrm{l}\mathrm{g}n)=\Theta (\mathrm{l}\mathrm{g}n)$。
　　再看递归式$T(n)=3T(n/4)+n\mathrm{l}\mathrm{g}n$。套用主定理，有$a=3,b=4$并且$f(n)=n\mathrm{l}\mathrm{g}n$，于是有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}3}=O(n^{0.793})$。所以有$f(n)=n\mathrm{l}\mathrm{g}n=\Omega (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a+\epsilon })$，其中$\epsilon \approx 0.2$。并且当$3/4\le c<1$时，有$af(n/b)=3f(n/4)=3•(n/4)•\mathrm{l}\mathrm{g}(n/4)=(3/4)•n\mathrm{l}\mathrm{g}(n/4)\le cf(n)=cn\mathrm{l}\mathrm{g}n$。所以可以应用主定理的情况3，从而得到解$T(n)=\Theta (f(n))=\Theta (n\mathrm{l}\mathrm{g}n)$。
　　最后看一个递归式$T(n)=2T(n/2)+n\mathrm{l}\mathrm{g}n$。套用主定理，有$a=2,b=2$并且$f(n)=n\mathrm{l}\mathrm{g}n$，于是有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{2}2}=n$。虽然$f(n)=n\mathrm{l}\mathrm{g}n$渐近大于$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n$，但并不是“多项式意义上的渐近大于”，即不存在$\epsilon >0$，使得$f(n)=\Omega (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a+\epsilon })$。因此这个递归式不能应用主定理求解。

练习

4.5-1 对下列递归式，使用主方法求出渐近紧确界。
　　a. $T(n)=2T(n/4)+1$
　　b. $T(n)=2T(n/4)+\sqrt{n}$
　　c. $T(n)=2T(n/4)+n$
　　d. $T(n)=2T(n/4)+n^2$
　　解
　　a.
　　应用主定理，根据递归式有$a=2,b=4,f(n)=1$，所以有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}2}=n^{1/2}$。于是有$f(n)=1=O(n^{1/2-\epsilon })=O(n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a-\epsilon })$，其中$\epsilon =1/2$。因此，可以应用主定理情况1，于是$T(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a})=\Theta (n^{1/2})$。
　　b.
　　应用主定理，根据递归式有$a=2,b=4,f(n)=\sqrt{n}=n^{1/2}$，所以有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}2}=n^{1/2}$。于是有$f(n)=n^{1/2}=\Theta (n^{1/2})=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a})$。因此，可以应用主定理情况2，于是$T(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}\mathrm{l}\mathrm{g}n)=\Theta (n^{1/2}\mathrm{l}\mathrm{g}n)$。
　　c.
　　应用主定理，根据递归式有$a=2,b=4,f(n)=n$，所以有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}2}=n^{1/2}$。于是有$f(n)=n=\Omega (n^{1/2+\epsilon })=\Omega (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a+\epsilon })$，其中$\epsilon =1/2$。并且当$1/2\le c<1$时，有$af(n/b)=2f(n/4)=2•(n/4)=n/2\le cf(n)=cn$。因此，可以应用主定理情况3，于是$T(n)=\Theta (f(n))=\Theta (n)$。
　　d.
　　应用主定理，根据递归式有$a=2,b=4,f(n)=n^2$，所以有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}2}=n^{1/2}$。于是有$f(n)=n^2=\Omega (n^{1/2+\epsilon })=\Omega (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a+\epsilon })$，其中$\epsilon =3/2$。并且当$1/8\le c<1$时，有$af(n/b)=2f(n/4)=2•(n/4{)}^2=n/8\le cf(n)=cn$。因此，可以应用主定理情况3，于是$T(n)=\Theta (f(n))=\Theta (n^2)$。

4.5-2 Caesar教授想设计一个渐近快于Strassen算法的矩阵相乘算法。他的算法使用分治法，将每个矩阵分解为n/4 × n/4的子矩阵，分解和合并步骤共花费$\Theta (n^2)$时间。他需要确定，他的算法需要创建多少个子问题，才能击败Strassen算法。如果他的算法创建$a$个子问题，则描述运行时间$T(n)$的递归式为$T(n)=aT(n/4)+\Theta (n^2)$。Caesar教授的算法如果要渐近快于Strassen算法，$a$的最大整数值应是多少？
　　解
　　对递归式$T(n)=aT(n/4)+\Theta (n^2)$应用主定理，有$b=4,f(n)=\Theta (n^2)$，所以有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}a}$。
　　Strassen算法的时间为$n^{\mathrm{l}\mathrm{g}7}$。要让新算法的时间小于$n^{\mathrm{l}\mathrm{g}7}$，必须满足$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}a}<n^{\mathrm{l}\mathrm{g}7}$，得到$a<49$。因此，$a$的最大值为$48$。

4.5-3 使用主方法证明：二分查找递归式$T(n)=T(n/2)+\Theta (1)$的解是$T(n)=\Theta (\mathrm{l}\mathrm{g}n)$。（二分查找的描述见练习2.3-5）。
　　解
　　应用主定理，根据递归式有$a=1,b=2,f(n)=\Theta (1)$，所以有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{2}1}=n^0=1$。于是有$f(n)=\Theta (1)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a})$。因此，可以应用主定理情况2，于是$T(n)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}\mathrm{l}\mathrm{g}n)=\Theta (\mathrm{l}\mathrm{g}n)$。

4.5-4 主方法能应用于递归式$T(n)=4T(n/2)+n^2\mathrm{l}\mathrm{g}n$吗？请说明为什么可以或者为什么不可以。给出这个递归式的一个渐近上界。
　　解
　　应用主定理，根据递归式有$a=4,b=2,f(n)=n^2\mathrm{l}\mathrm{g}n$，所以有$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{2}4}=n^2$。虽然$f(n)=n^2\mathrm{l}\mathrm{g}n$渐近大于$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a}=n^2$，但不是多项式意义上的渐近大于，即不存在$\epsilon >0$，使得$f(n)=\Omega (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{b}a+\epsilon })$。因此该递归式不能应用主定理求解。考虑用递归树方法求解。创建递归树，如下图所示。
　　
　　在递归树中，深度为$i$的结点对应规模为$n/2^i$的子问题。当$n/2^i=1$时，即$i=\mathrm{l}\mathrm{g}n$时，子问题规模变为$1$，这对应于叶结点$T(1)$，因此树的高度$h=\mathrm{l}\mathrm{g}n$。
　　每层的结点数都是上一层的$4$倍，因此深度为$i$的结点数为$4^i$。深度为$i$的结点对应的子问题规模为$n/2^i$，除叶结点外，深度为$i$的每个结点的代价为$(n/2^i{)}^2•\mathrm{l}\mathrm{g}(n/2^i)$。因此，除叶结点外，深度为$i$的所有结点的代价为$4^i•(n/2^i{)}^2•\mathrm{l}\mathrm{g}(n/2^i)=n^2•\mathrm{l}\mathrm{g}(n/2^i)=n^2(\mathrm{l}\mathrm{g}n-i)$。叶结点一共有$4^{\mathrm{l}\mathrm{g}n}=n^2$个，所以叶结点那一层的代价为$\Theta (n^2)$。
　　现在将每一层的代价加起来，得到
　　
　　下面用代入法验证这一结果。我们要证明的是：存在正常数$c$，使得$T(n)\le c{n}^2{\mathrm{l}\mathrm{g}}^{2}n$对足够大的$n$都成立。
　　取初始情况$T(1)=1$。无论取$c$为多少，都不能使得$T(1)\le c•1^2•{\mathrm{l}\mathrm{g}}^{2}1=0$成立。于是我们要取初始情况为$T(2)$。根据递归式，有$T(2)=4T(1)+1^2•\mathrm{l}\mathrm{g}1=4$。只要取$c\ge 1$，就能使得$T(2)\le c•2^2•{\mathrm{l}\mathrm{g}}^{2}2=4c$成立。
　　现在考虑$n\ge 3$的情况。假设$T(n)\le c{n}^2{\mathrm{l}\mathrm{g}}^{2}n$对$2,3,\dots ,n-1$都成立，于是有
　　
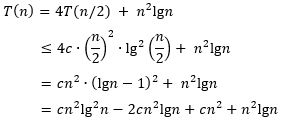
　　现在要选取合适的$c$，使得不等式$c{n}^2{\mathrm{l}\mathrm{g}}^{2}n-2c{n}^2\mathrm{l}\mathrm{g}n+c{n}^2+n^2\mathrm{l}\mathrm{g}n\le c{n}^2{\mathrm{l}\mathrm{g}}^{2}n$成立。对该不等式做一下变换。
　　
　　当$n\ge 3$时，$\frac{1}{2-1/\mathrm{l}\mathrm{g}n}$是单调递减的，并且在$n=3$时取得最大值$\frac{1}{2-{\mathrm{l}\mathrm{o}\mathrm{g}}_{3}2}$。因此，只要取$c\ge \frac{1}{2-{\mathrm{l}\mathrm{o}\mathrm{g}}_{3}2}$，就能使得不等式$c{n}^2{\mathrm{l}\mathrm{g}}^{2}n-2c{n}^2\mathrm{l}\mathrm{g}n+c{n}^2+n^2\mathrm{l}\mathrm{g}n\le c{n}^2{\mathrm{l}\mathrm{g}}^{2}n$成立，此时$T(n)\le c{n}^2{\mathrm{l}\mathrm{g}}^{2}n$成立。
　　综合考虑初始情况$T(2)$，我们最终要取$c\ge 1$。于是$T(n)=O(n^2{\mathrm{l}\mathrm{g}}^{2}n)$得证。

4.5-5 考虑主定理情况3的一部分：对某个常数$c<1$，正则条件$af(n/b)\le cf(n)$是否成立。给出一个例子，其中常数$a\ge 1，b>1$且函数$f(n)$满足主定理情况3中除正则条件外的所有条件。
　　略