算法导论 — 6.5 优先队列

笔记

本节介绍堆的另外一种重要应用：优先队列。一个最大堆构成最大优先队列，同样一个最小堆构成最小优先队列。本节主要探讨最大优先队列。
　　一般来说，优先队列中的每个元素都有一个关键字(key)。关键字决定了一个元素在优先队列中的位置。一个最大优先队列支持以下操作：
　　• INSERT(S, x)：把元素$x$插入最大优先队列$S$中。
　　• MAXIMUM(S)：返回$S$中具有最大关键字的元素。
　　• EXTRACT-MAX(S)：去掉并返回$S$中具有最大关键字的元素。
　　• INCREASE-KEY(S, x, k)：将元素$x$的关键字增加到$k$，这里$k$不能小于$x$的原关键字。
　　MAXIMUM操作很简单，直接返回堆中的第一个元素，时间为$\Theta (1)$。
　　
　　EXTRACT-MAX先保存队列中的最大元素$A[1]$，然后将末尾元素移到$A[1]$位置，再调用MAX-HEAPIFY来维持最大堆的性质，最后返回保存下来的最大元素。
　　
　　MAX-HEAP-EXTRACT-MAX的时间取决于MAX-HEAPIFY的调用，其他操作都只需要花费常数时间，因此时间复杂度为$O(lgn)$。
　　INCREASE-KEY将某个元素的关键字增大，该元素有可能违返堆的性质。为保持堆的性质，将当前元素不断与其父结点进行比较，如果当前元素较大，则将当前元素与父结点进行交换。这一过程不断重复，直到当前元素不大于其父结点为止，或直到当前元素已经上溯到堆首元素为止。
　　
　　MAX-HEAP-INCREASE-KEY的运行时间取决于while循环，该循环的次数不超过堆的高度，故时间复杂度为$O(\mathrm{l}\mathrm{g}n)$。下图给出了一个MAX-HEAP-INCREASE-KEY的例子。
　　
　　INSERT先在堆尾增加一个关键字为$-\infty$的元素，然后调用INCREASE-KEY将这个元素的关键字增加为需要插入的关键字，同时保持堆的性质。
　　
　　显然，MAX-HEAP-INSERT的时间复杂度也为$O(\mathrm{l}\mathrm{g}n)$。

练习

6.5-1 试说明MAX-HEAP-EXTRACT-MAX在堆A = <15, 13, 9, 5, 12, 8, 7, 4, 0, 6, 2, 1>上的操作过程。
　　解
　　

6.5-2 试说明MAX-HEAP-INSERT(A, 10)在堆A = <15, 13, 9, 5, 12, 8, 7, 4, 0, 6, 2, 1>上的操作过程。
　　解
　　

6.5-3 要求用最小堆实现最小优先队列，请写出MIN-HEAP-MINIMUM、MIN-HEAP-EXTRACT-MIN、MIN-HEAP-DECREASE-KEY和MIN-HEAP-INSERT的伪代码。
　　解
　　

6.5-4 在MAX-HEAP-INSERT的第2行，为什么我们要先把关键字设为$-\infty$，然后又将其增加到所需要的值呢？
　　解
　　MAX-HEAP-INSERT通过调用MAX-HEAP-INCREASE-KEY来实现所需的功能。把关键字设为$-\infty$，是为了在调用MAX-HEAP-INCREASE-KEY时，使得$key>A[A.heap\_size]$一定成立，这样保证程序会继续执行，而不会返回error。

6.5-5 试分析在使用以下循环不变式时，MAX-HEAP-INCREASE-KEY的正确性。
　　在算法的第4~6行while循环每次迭代开始的时候，子数组$A[1..A.heap\_size]$要满足最大堆的性质。如果有违背，只有一个可能：$A[i]$大于$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]$。
　　这里，你可以假设在调用MAX-HEAP-INCREASE-KEY时，$A[1..A.heap\_size]$是满足最大堆性质的。
　　解
　　(1) 初始化
　　调用MAX-HEAP-INCREASE-KEY前，$A[1..A.heap\_size]$已经是一个最大堆，满足最大堆的性质。MAX-HEAP-INCREASE-KEY一开始将$A[i]$赋值为$key$。进入循环之前，只有$A[i]$的值发生了变化，并且$A[i]$的值是增大的。此时$A[i]$仍然比它的子树中的结点要大，以$A[i]$为根的子树依然满足最大堆的性质。但是$A[i]$有可能会超过它的父结点，此时最大堆的性质不被满足。因此，进入循环之前，只可能出现$A[i]>A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]$的情况，使得最大堆的性质不被满足。故在迭代开始之前，循环不变式为真。
　　(2) 保持
　　假设在进入迭代$i$之前，循环不式为真。在进迭代$i$的时候，会判断$A[i]$和$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]$的大小关系。如果$A[i]>A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]$，那么交换$A[i]$和$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]$，即将较大的元素交换到上一层，将较小的元素交换到下一层，使$A[i]$和$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]$这两个位置满足最大堆的性质。此时$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]$变大了，那么$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]$有可能会超过它的父结点，从而破坏最大堆的性质。而堆的其他部分都已满足最大堆的性质。因此，在进入下一次迭代$\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)$之前，循环不变式也为真。
　　(3) 终止
　　循环终止条件有两个：$i=1$或者$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]\ge A[i]$，二者至少有一个成立即终止循环。
　　先看由于$i=1$而循环终止的情况。此时循环不变式应当为真。将$i=1$代入循环不变式中，得到“子数组$A[1..A.heap\_size]$满足最大堆的性质。如果有违背，只有一个可能：$A[1]$大于$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(1)]$”。由于$A[1]$已经是最大堆的根结点，它的父结点不存在，所以“$A[1]$大于$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(1)]$”这一违背最大堆性质的情况是不存在的。因此$A[1..A.heap\_size]$完全满足最大堆的性质。
　　再看由于$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]\ge A[i]$而循环终止的情况。根据循环不变式，只可能出现$A[i]>A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]$的情况，使得最大堆的性质不被满足。然而根据循环终止条件，又有$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]\ge A[i]$。故唯一的违背最大堆性质的情况也不存在。因此，此时$A[1..A.heap\_size]$完全满足最大堆的性质。

6.5-6 在MAX-HEAP-INCREASE-KEY的第5行的交换操作中，一般需要通过三次赋值来完成。想一想如何利用INSERTION-SORT内循环部分的思想，只用一次赋值就完成这一交换操作？
　　解
　　

6.5-7 试说明如何使用优先队列来实现一个先进先出队列，以及如何使用优先队列来实现栈。
　　解
　　这里只给出思路，不赘述详细的实现过程。无论是先进先出的队列，还是后进先出的栈，一个元素在入队或入栈时，给它赋予一个关键字$key$。越是先入队或先入栈的元素，关键字$key$越小；而越是晚入队或晚入栈的元素，关键字$key$越大。例如，我们可以用入队或入栈的时间作为$key$值。
　　基于以上规定，我们可以用最小优先队列来实现先进先出队列。入队最早的元素，其$key$值最小，通过调用MIN-HEAP-EXTRACT-MIN可以让它最先被取出。
　　相反，用最大优先队列来实现后进先出的栈。入队最晚的元素，其$key$值最大，通过调用MAX-HEAP-EXTRACT-MAX可以让它最先被取出。

6.5-8 MAX-HEAP-DELETE(A, i)操作能够将结点$i$从堆$A$中删除。对于一个包含$n$个元素的堆，请设计一个能够在$O(\mathrm{l}\mathrm{g}n)$时间内完成的MAX-HEAP-DELETE操作。
　　解
　　将要删除的元素$A[i]$和堆的最后一个元素$A[A.heap\_size]$交换，再将$A[A.heap\_size]$删除。如此处理之后，堆的性质可能被破坏。根据$A[i]$和$A[A.heap\_size]$的大小关系分为两种情况：
　　1) $A[A.heap\_size]\le A[i]$
　　此时，交换$A[i]$和$A[A.heap\_size]$后，以$A[i]$为根的子树有可能不满足堆的性质，调用MAX-HEAPIFY即可。
　　2) $A[A.heap\_size]>A[i]$
　　此时，交换$A[i]$和$A[A.heap\_size]$后，$A[i]$有可能比其父结点$A[\mathrm{P}\mathrm{A}\mathrm{R}\mathrm{E}\mathrm{N}\mathrm{T}(i)]$要大。可以采用类似HEAP-INCREASE-KEY的方式来将$A[i]$向上移动到正确的位置。或者不用交换$A[i]$和$A[A.heap\_size]$，直接对元素$i$调用HEAP-INCREASE-KEY(A, i, A[A.heap_size])，然后将$A[A.heap\_size]$删除。
　　无论是情况1)调用MAX-HEAPIFY，还是情况2)调用HEAP-INCREASE-KEY(A, i, A[A.heap_size])，都要花费$O(\mathrm{l}\mathrm{g}n)$时间。
　　
　　笔者有在网上看到过下面这种解法。这种解法的本意是将要删除的元素变成$-\infty$，然后调用MAX-HEAPIFY(A, i)，希望将$-\infty$一直交换到堆的末尾位置，最后将$heap\_size$减1，即可实现删除元素。然而调用MAX-HEAPIFY(A, i)最终会将$-\infty$交换到某一个叶结点上，并不一定是堆的末尾。因此，这种解法是错误的。希望读者不要被误导。
　　

6.5-9 请设计一个时间复杂度为$O(n\mathrm{l}\mathrm{g}k)$的算法，它能够将$k$个有序链表合并为一个有序链表，这里$n$是所有输入链表包含的总的元素个数。（提示：使用最小堆来完成$k$路归并。）
　　解
　　为了将$k$个有序链表合并，我们需要比较每个链表各自的最小元素，也即比较每个链表的首端元素，从中取出最小者插入到输出链表中，并将这个最小者从它原本所在的链表中删除。然后如此循环迭代，即可将$k$个链表合并。
　　为了比较每个链表各自的最小元素，我们维护一个大小为$k$的最小堆$H$。最小堆$H$中始终包含每个链表当下的最小元素。具体算法如下。
　　我们假定每个链表都非空。首先从$k$个链表中分别取出第$1$个元素，构成一个大小为$k$的最小堆$H$，将每个元素的$key$保存在$H[i].key$中。此时堆中的元素分别是$k$个链表各自的最小元素，并且堆的根结点是所有$k$个链表范围内的最小元素。建堆的过程中，我们需要记住每个元素$i$来自哪个链表，用$H[i].index$来表示$(1\le H[i].index\le k)$。然后我们新建一个空链表$L_M$。
　　现在进入迭代过程。每次迭代先调用MIN-HEAP-EXTRACT-MIN取出最小堆$H$中的最小元素，插入到新建链表$L_M$的末尾。我们事先会记下取出的元素来自哪个链表，再从相同的这个链表中取出第$1$个还未被取出过的元素，插入到$H$中，以维持“最小堆$H$中始终包含每个链表当下的最小元素”这一条件。如果我们在准备从一个链表中取出元素插入到$H$中时，该链表的所有元素都已经被取出过，那么不执行插入，并将最小堆$H$的大小减$1$。然后进入下一次迭代。直到$k$个链表中的所有元素都被取出过，并且最小堆$H$中已经没有元素为止。
　　
　　该算法的运行时间取决于while循环。while循环中有3个操作：PUSH-BACK、MIN-HEAP-EXTRACT-MIN和MIN-HEAP-INSERT。后两者分别都需要花费$O(\mathrm{l}\mathrm{g}k)$的时间。现在我们来确定PUSH-BACK的时间。一般情况下，单链表的PUSH-BACK操作需要$O(n)$的时间，因为需要从表头遍历到表尾，才能找到表尾所在的位置，并将元素连接在表尾。然而这里的PUSH-BACK是处在一个while循环中，每次迭代可以用一个指针记录下表尾的位置，这样每次PUSH-BACK只需花费常数时间。因此每次while迭代的时间为$O(\mathrm{l}\mathrm{g}k)$。while迭代的次数应当等于所有元素的个数$n$。这样，该算法总的时间复杂度就是$O(n\mathrm{l}\mathrm{g}k)$。
　　下图给出了一个合并3个链表的例子。
　　
　　
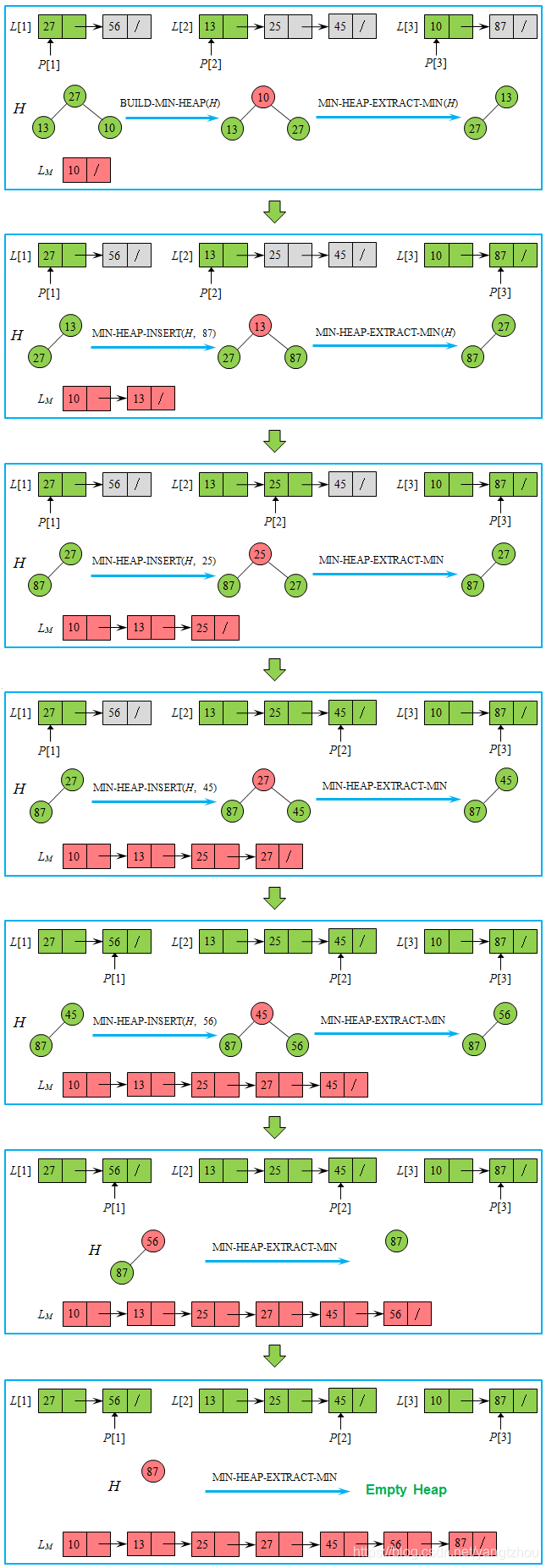
　　以下是最大优先队列的代码链接。
　　https://github.com/yangtzhou2012/Introduction_to_Algorithms_3rd/tree/master/Chapter06/Section_6.5