APSO（自适应粒子群算法）学习

最新推荐文章于 2025-03-06 22:04:57 发布

紫26

最新推荐文章于 2025-03-06 22:04:57 发布

阅读量6.6k

点赞数 4

文章标签：学习算法

本文链接：https://blog.csdn.net/yangzai0326/article/details/130195598

版权

PSO（粒子群优化算法）介绍

PSO模仿鸟类群集和鱼类集群的群体行为，引导粒子搜索全局最优解。标准PSO算法在解决复杂的多峰问题容易陷入局部最优解。因此，加快收敛速度和避免陷入局部最优解已成为粒子群算法研究中两个最重要和最具吸引力的目标。最有前景的解决方法是控制算法参数和与辅助搜索算子结合。APSO为实现这两个目标而产生。

PSO及其发展

PSO框架

在PSO中，一群粒子被表示为潜在解，并且每个粒子i与两个向量相关联，即，速度矢量Vi=[v1i,v2i,...,vDi]和位置向量Xi=[x1i,x2i,...,xDi]，其中D代表解空间的维度。每个粒子的速度和位置由相应范围内的随机向量初始化。在演化过程中，粒子i在维度d上的速度和位置更新为：

$v^{_{i}^{d}}=wv^{_{i}^{d}}+c_{1}rand^{_{1}^{d}}(pBest_{i}^{d} - x^{_{i}^{d}})+c_{2}rand^{_{2}^{d}}(nBest_{i}^{d}-x^{_{i}^{d}})$

$x^{_{i}^{d}}=x^{_{i}^{d}}+v^{_{i}^{d}}$

其中w是惯性权重，c1和c2是加速度系数，rand1d和rand2d是在第d维的[0,1]内独立生成的两个均匀分布的随机数。pBesti是针对第i个粒子找到的具有最佳适应度的位置，nBest是邻域的最佳位置。

$V_{max}^{d}\in R^{+}$

上式表示每个粒子的最大速度钳制在第d维上。如果更新的速度大小 $\left | v^{_{i}^{d}} \right |$ 超过 $V_{max}^{d}$ ，则 $v^{_{i}^{d}}$ 赋值为 $sign(v^{_{i}^{d}})V^{_{max}^{d}}$ .最大速度建议取搜索范围的20%。

PSO研究进展

有人对惯性权重w提出随迭代逐渐线性下降的公式：

$w=w^{_{max}}-(w^{_{max}}-w^{_{min}})\frac{g}{G}$

其中g表示当前进化迭代数的迭代索引，G是预定义的最大迭代数，wmax和wmin通常设置为0.9和0.4.

有人提出了模糊自适应w，将w设置为0.5+random(0,1)/2的随机版本，用于动态系统优化。由于这个w的期望值是0.75，有人为了分析粒子群算法的收敛性，引入了收缩因子，见下式：

$v^{_{i}^{d}}=\chi [v^{_{i}^{d}}+c_{1}rand^{_{1}^{d}}(pBest_{i}^{d} - x^{_{i}^{d}})+c_{2}rand^{_{2}^{d}}(nBest_{i}^{d}-x^{_{i}^{d}})]$

其中收缩因子

$\chi =\frac{2}{\left | 2-\varphi -\sqrt{\varphi ^{2 }-4\varphi } \right |}$

设置为0.729，其中

$\varphi =c_{1}+c_{2}=4.1$

其中c1和c2均设置为2.05，在数学上，收缩因子等同于惯性权重。

针对c1和c2，有人建议固定值为2.0，有人使用c1和c2的临时值而不是固定值2.0，也有人提出一种具有线性时变加速系数的PSO算法（HPSO-TVAC），开始时设置较大的c1和较小的c2，并在搜索过程中逐渐反转。效果最好的是HPSO-TVAC方法。

PSO的ESE

一、粒子群算法中的种群分布信息

步骤一：在当前位置，计算每个粒子i到所有其他粒子的平均距离。例如，可使用欧几里得度量来测量该平均距离。

$d_{i}=\frac{1}{N-1}\sum_{j=1,j\neq i}^{N}\sqrt{\sum_{k=1}^{D}(x_{i}^{k}-x_{j}^{k})^{2}}$

其中N和D分别是群体大小和维度的数量。

步骤二：将全局最佳粒子的di表示为dg。比较所有di，并确定最大和最小距离dmax和dmin。计算由下式定义的进化因子f：

$f=\frac{d_{g}-d_{min}}{d_{max}-d_{min}}\in [0,1]$

步骤三：将f分类到四个集合S1,S2,S3和S4中的一个，这四个集合分别表示探索、利用、收敛和跳出的状态。

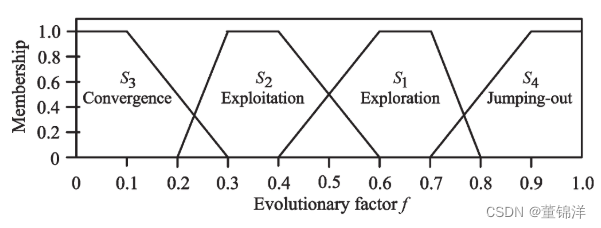
利用模糊函数定义如下：

（1）探索——f的中到大值表示S1，其隶属函数定义为：

（2）利用——f的收缩值表示S2，其隶属函数定义为：

（3）收敛——f的最小值表示S3，其隶属函数定义为：

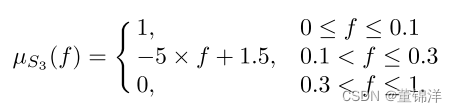
（4）跳出——f的最大值反映S4，其隶属函数定义为：

APSO

粒子群参数的自适应控制

1.惯性权重的自适应

粒子群算法中的惯性权重w用于平衡全局和局部搜索能力。惯性权重w与演化因子f有关，则允许w使用S形映射w(f)：

$w(f)=\frac{1}{1+1.5e^{-2.6f}}\in [0.4,0.9], \forall f\in [0,1].$

2.加速系数的控制

参数c1代表自我认知，将粒子拉到自己的历史最佳位置；参数c2表示社会影响，推动群体收敛到当前的全局最佳区域，帮助快速收敛。加速系数被初始化为2.0，并根据进化状态进行自适应控制，策略如下：

（1）策略一——在探索状态下增加c1和减少c2。此策略可帮助粒子单独探索并实现它们自己的历史最佳位置，而不是拥挤在可能与局部最优相关联的当前最佳粒子周围。

（2）策略二——在利用状态下略微增加c1并略微减少c2。

（3）策略三——在收敛状态下略微增加c1并略微增加c2。

（4）策略四——在跳出状态下减少c1并增大c2。

3.加速度系数的界限

两代之间的最大增量或减量由下式限定：

$\left |c _{i}(g+1)- c _{i}(g)\right |\leq \delta ,i=1,2$

其中 $\delta$ 被称为加速率，在区间[0.05,0.1]中均匀生成的 $\delta$ 随机值在大多数测试函数上表现最好。在策略2和策略3中建议使用0.5 $\delta$ ，建议轻微更改。

[1.5,2.5]被选择为c1和c2的区间。建议[3.0,4.0]用于限制两个参数的总和。如果c1和c2总和大于4.0，则c1和c2归一化为

$c_{i}=\frac{c_{i}}{c_{1}+c_{2}}4.0,i=1,2$

ELS

ELS随机选择gBest的历史最佳位置的一个维度，其由第d维度的pd表示。

$P_{d}=P_{d}+(X_{max}^{d}-X_{max==min}^{d})\cdot Gaussian(\mu ,\sigma ^{2})$

$\sigma =\sigma _{max}-(\sigma _{max}-\sigma _{min})\frac{g}{G}$

其中 $\sigma _{max}$ 和 $\sigma _{min}$ 是 $\sigma$ 的上界和下界， $\sigma _{max}$ =1.0和 $\sigma _{min}$ =0.1在大多数测试函数上都有良好的性能。

APSO的搜索行为

使用群体标准差psd比较APSO和传统PSO搜索的多样性：

$psd=\sqrt{[\sum_{i=1}^{N}\sum_{j=1}^{D}(x_{i}^{j}-\bar{x}^{j})^{2}]/(N-1)}$

其中N、D和x分别是所有粒子的总体大小、维数和平均位置。

如果psd很小，说明种群已经紧密地向某一区域收敛，种群的多样性较低；psd值越大，表明种群多样性越高。

参考文献：

Zhi-Hui Zhan, Jun Zhang, Yun Li,et al.Adaptive Particle Swarm Optimization[C].IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS—PART B: CYBERNETICS, VOL. 39, NO. 6,Sep.2009,pp:1362-1381.