介绍
我们知道,PCA是用于对数据做降维的,我们一般用PCA把m维的数据降到k维(k < m)。
那么问题来了,k取值多少才合适呢?
PCA误差
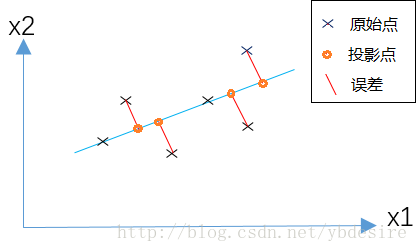
PCA的原理是,为了将数据从n维降低到k维,需要找到k个向量,用于投影原始数据,是投影误差(投影距离)最小。
用公式来表示,如下
其中
- m表示特征个数
分子表示原始点与投影点之间的距离之和,而误差越小,说明降维后的数据越能完整表示降维前的数据。如果这个误差小于0.01,说明降维后的数据能保留99%的信息。
k值选取的原理
实际应用中,我们一般根据上式,选择能使误差小于0.01(99%的信息都被保留)或0.05(95%的信息都被保留)的k值。
而在实际编码中,参考文章《详解主成分分析PCA》,在PCA的实现过程中,对协方差矩阵做奇异值分解时,能得到S矩阵(特征值矩阵)。
PCA误差的表达式等效于下式
从代码示例中,可以看出,将数据从三维降到二维,保留了99.997%的信息。
[U,S,V] = np.linalg.svd(sigma) # 奇异值分解
(S[0]+S[1])/(S[0]+S[1]+S[2])
# result = 0.99996991682077252实际使用
用sklearn封装的PCA方法,做PCA的代码如下。PCA方法参数n_components,如果设置为整数,则n_components=k。如果将其设置为小数,则说明降维后的数据能保留的信息。
from sklearn.decomposition import PCA
import numpy as np
from sklearn.preprocessing import StandardScaler
x=np.array([[10001,2,55], [16020,4,11], [12008,6,33], [13131,8,22]])
# feature normalization (feature scaling)
X_scaler = StandardScaler()
x = X_scaler.fit_transform(x)
# PCA
pca = PCA(n_components=0.9)# 保证降维后的数据保持90%的信息
pca.fit(x)
pca.transform(x)所以在实际使用PCA时,我们不需要选择k,而是直接设置n_components为float数据。
总结
PCA主成分数量k的选择,是一个数据压缩的问题。通常我们直接将sklearn中PCA方法参数n_components设置为float数据,来间接解决k值选取问题。
但有的时候我们降维只是为了观测数据(visualization),这种情况下一般将k选择为2或3。










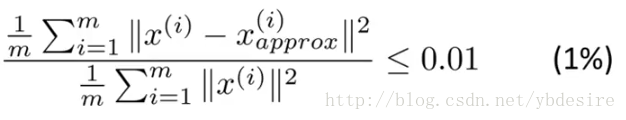
















 2490
2490

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








