语言模型学习（01）传统统计语言模型以及初期的神经网络语言模型+Perplexity介绍

语言模型

什么是语言模型？
        对于语言序列(w₁,w₂,…,w_n),语言模型就是计算该序列的概率，即P(w₁,w₂,…,w_n)
通俗的来说，就是随便由n个词组成的一句话s,可以通过语言模型来判断这句话是不是“人话”.
这句话“越像人话”，那么语言模型就会给该句子一个偏大的概率，“越不像人话”则语言模型就会给该句子一个偏小的概率。
        例如：p(I love you)>p(I you love)

        语言模型可分为统计语言模型以及现在常用的神经网络语言模型，下面将依次分别进行介绍。

统计语言模型

        从第一章我们可以知道，语言模型就是计算P(w₁,w₂,…,w_N)。
        根据概率的乘法公式，其计算公式可由如下表达式进行描述：

                                        P(w₁,w₂,…,w_N)=P(w₁)*P(w₂|w₁)…*P(w_N|w₁,w₂,…,w_N-1)。
        而在统计语言模型当中，我们采取的是极大似然估计来计算这其中每一个词的条件概率，即：

                                        $$P(wN|w1,w2,...,w(N-1))=\frac{Count(w1,w2,...,wN)}{Count(w1,w2,...,w(N-1))}$$
        其中Count函数表示子序列在训练集当中出现的次数。但是直接使用上述公式来计算 P(w_n|w₁,w₂,…,w_(N-1))是不现实的。有如下两个原因：
        (1):参数空间过大。对于P(w_N|w₁,w₂,…,w_(N-1))，我们将其称为N元模型(N-Gram Model)，由于句子中的字符全部来源于字典V，假设其大小为|V|,那么该n元模型的自由参数量为|V|^N。显然看出自由参数量随着N的增大呈现指数性增加。
        (2):数据过于稀疏。我们若通过上述公式对实际的句子进行评估的时候，发现计算出来的结果可能几乎全部为0，原因在于语料库的规模有限，而实际的句子是不受限的。因此实际中的很多的词对组合可能在语料库中都不会出现。最后造成数据稀疏的情况。

        针对问题(1):我们在实际的应用当中，引入马尔科夫假设，假设当前词出现的概率只依赖于前n-1个词。即
                        P(w_N|w₁,w₂,…,w_(N-1))=P(w_N|w_N-n+1,w_N-n+2,…,w_(N-1))

        而为了方便计算对于n我们也是往往取一个小的整数(一般为(1,2,3))。基于此我们一般在计算n-gram语言模型的时候，一般都是使用如下的三种类型：

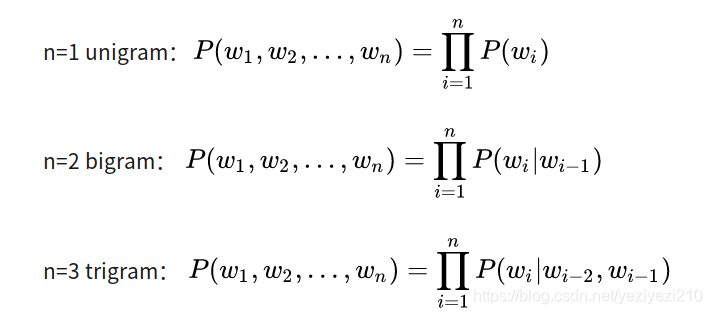
        另外,在实际使用n-gram模型的时候需要注意的是，为了方便计算以及使得计算的概率和为1。我们往往会在每一句话的首尾分别加上起始符< s >和中止符< /s >。前者是为了表征句子首个单词出现的条件概率，即：
                                                        P(W₁)=P(W₁|< s >)

        而后者是为了使得在对任意长度的序列进行建模的时候，都能保证所有的概率和为1。

        针对问题(2)我们常常采用平滑的方式(Smooth)来解决。这里举一种平滑方式，即在计算的时候，将分子分母同时都加1，这样的话就不会再出现概率为0的情况了，表达式为：
$$P(wN|w1,w2,...,w(N-1))=\frac{Count(w1,w2,...,wN)+1}{Count(w1,w2,...,w(N-1))+1}$$
        其他的平滑方式如 Laplace Smoothing；Kneser-Ney等等也是经常使用，有兴趣的可以自己去了解。

        对于N-gram模型，这里做一个简单的总结：
                优点：（1）使用极大似然估计，参数容易训练。
                            （2）可解释性好，模型直观，容易理解。
                缺点：（1）只能依赖于前n个词来进行建模，缺乏长期依赖。
                            （2）随着n的增大，参数的数量呈指数形式上升。
                            （3）模型仅仅依赖统计词组频率，不具有好的泛化性。

初期的神经网络语言模型

        在本章仅介绍一些初期的神经网络语言模型如：NNLM，以及RNN based on language model。

      NNLM

        NNLM是03年Bengio提出来的基于前馈神经网络的语言模型。其具体结构如下图所示：
                                                                        图1：NNLM结构图

        在本博客最初的时候我们提到，语言模型的目的就是求解P(w₁,w₂,…,w_N)。而从统计语言模型的内容当中我们得知，P(w₁,w₂,…,w_N)的关键在于求解 P(w_t|w₁,w₂,…,w_(t-1))因此，该NNML模型的关键也就是在于求解t时刻的单词w_t的概率预测。

        NNLM训练的模型的数学表达式为

        f(w_t,w_t-1,…,w_t-n+1)=P(w_t|context)；其中context代表从1到t-1的词.

        含义是从语料库当中选择一系列长度为n-1的文本序列(w_t-1,…,w_t-n+1)，组成训练集D然后进行对第t个单词w_t的概率的推测。

        在这个模型当中,可以理解其由两个部分组成:

        1:一个维度为|V|*m的矩阵C,其中|V|为训练集字典的维度,m为表示代表单词w_i的特征向量的长度.即字典中的每一个单词都能从矩阵C中找到相对应的特征向量.上述过程即图中第一层到第二层的过程，

        2:将条件概率的函数表示如下:
                                        f(i,w_t-1,…,w_t-n+1)=g(i,C(w_t-1),…,C(w_t-n+1))

        即该函数是用来估计P(w_t=i|context).其中i有|V|种取值.如果把该神经网络模型的参数记做$\omega$,那么整个模型的参数为$\theta$=(C,$\omega$).我们在训练该模型参数的时候就是将下面的似然函数极大化:

                                        L=$\frac{1}{T}$${\sum }_t$log(f(w_t,w_t-1,…,w_t-n+1;$\theta$))+R($\theta$)

        而图1中的整体计算流程如下所示，即：

                                        y=b+Wx+Utanh(d+Hx)
        其中Wx表示输入层与输出层之间有直接联系，如果不要这个链接。我们可以直接设置W为0即可；b为输出层的偏置向量，d为隐藏层的偏置向量，而公式中的x即为单词到特征向量的映射，计算如下：

                                        x=(C(w_t-1),C(w_t-2),…,C(w_t-n+1))

      隐藏层神经元的个数为h，那么整个模型的参数表示可以从$\theta$=(C,$\omega$)细化为$\theta$=(b,d,W,U,H,C)。在实际的训练过程当中，我们通过计算该模型预测出来的t时刻的单词w_t和真实的label进行比较，计算二者的loss，之后再通过反向传播的方式来进行模型参数$\theta$的更新。这就是最初的神经网络语言模型。

      作者利用神经网络去建模当前词出现的概率与其前 n-1 个词之间的约束关系。很显然这种方式相比 n-gram 具有更好的泛化能力，只要词表征足够好(即矩阵C设计合理)。就能很大程度地降低了数据稀疏带来的问题。但是这个结构的明显缺点是仅包含了有限的前文信息（即前文信息的长度是在训练前被固定的）。为了解决这种定长信息问题，循环神经网络便开始被投入语言模型的训练。

      RNN based on language model

                                    RNN language model 图
        图中输入层到RNN层之间也会经过词嵌入的方式将词汇转化成为词向量然后再输入RNN当中。在每个time_step都会将词汇表V中的所有单词都计算一遍概率。然后会输出最高概率所对应的单词。其中<s>和</s>为起始符和中止符号。图中输出层的概率计算可以看作是p(w|<s>),p(w|<s>我)，p(w|<s>,我爱)，p(w|<s>,我爱你)。训练的时候我们的目标则是使这些条件概率尽可能的大，以此来训练语言模型。当使用该语言模型对某句话进行评估的时候，则使用RNN每一个time_step输出的概率值的乘积来表示该句子的合理性(即这句话是"人话"的概率)。该神经网络训练参数的方式也和NNLM一致，也都是通过对模型输出和Label的损失做反向传播来更新参数，在此不做复述。

      语言模型评估准则Perplexity

      在上述语言模型的叙述过程当中，我们说语言模型是评估一句话是不是“人话”的概率。那么这个评估的越准确，则模型就越好。我们知道，语言模型的评价标准就是句子是人话的概率，下面将以一个例子进行说明
      假设测试语料中共包括m个句子，第$i$个句子中有$n_i$个词，那么，$$M=\sum _{i=1}^m{n}_i$$
      对于每一个句子$x^{(i)}$，若$$\prod _{i=1}^{m}p(x^{(i)})$$越大，则说明语言模型在测试语料上表现的越好。为了方便起见，上述的概率连乘的形式可以改为如下评价标准
$$l=\frac{1}{M}\sum _{i=1}^{m}lo{g}_{2}p(x^{(i)})$$
      而语言模型的评价标准困惑度（Perplexity）就是上述式子的指数形式，表示为：
$$PPL=2^{-l}$$

      上述式子是困惑度最为常见的表述形式,为了进一步了解该指标，下面将详细介绍下困惑度的知识。
      首先直接说结论，困惑度是交叉熵（Cross Entropy）的指数形式。交叉熵是我们在训练模型的时候常用的一个损失函数的形式。交叉熵的一般表达式可以下式进行表示(离散形式)
                                    $$H(p,q)=-\sum _{i}p(i)log(q(i))$$
      其中p为真实分布，q为模型的预测的分布。
      在语言模型当中，对于语言L，L中的每一个字都可以看作是一个离散的随机变量，那么L就是一个离散的随机变量的序列。故L可以当作一个随机过程
在序列L当中，我们所计算的交叉熵也必须和L的有关，因此需要一个随机变量序列的熵随 L的长度n 的变化情况的指标。该指标也称为熵率。熵率的定义如下所示      因此当我们去计算语言L的交叉熵的时候，根据熵率的定义，我们可将语言L的交叉熵定义如下：                                          
$$H(p,q)=-\underset{n\to +\infty }{\lim }\frac{1}{n}\sum _{L}P(w_1,...,w_n)logQ(w_1,...,w_n)$$                                                                                                                  

然后根据 Shannon-McMillan-Breiman定理，式1可以近似写作：
$$H(p,q)=-\underset{n\to +\infty }{\lim }\frac{1}{n}logQ(w_1,...,w_n)$$                                                                                                                  
      此外，由于语言模型所用语料，单词序列都很长，因此，式2也可近似写成如下样子：$$H(p,q)=-\frac{1}{n}logQ(w_1,...,w_n)$$                                                                                                                  

      故在模型训练中所用交叉熵可用式3来进行近似替代。
      在使用训练数据训练得到语言模型之后，我们便可以来计算Perplexity来衡语言模型的好坏。假设测试的语料为$ϵ$,测试语聊中的每一语句为单词序列 E = {e₁,e₂,…,e_m}则根据式3，其交叉熵写为
$$H(ϵ)=\frac{1}{{\sum }_{E\in ϵ}|E|}\sum _{E\in ϵ}lo{g}_{2}Q(E)$$                                                                                                                  

      这和式3其实是一种形式，式3是将整个语言L写了进去，而式4是将语料$ϵ$分成了很多单句，因此，加上$\sum$以后就是整个语料了。所以实质是一样的。
      本小结的最初提到Perplexity是交叉熵的指数形式，因此语言模型的交叉熵可写为：$$PPL(ϵ)=2^{H(ϵ)}$$
      更据上述的ppl的表达式，便可以求出训练好的语言模型的困惑度。

参考文献

求通俗解释NLP里的perplexity是什么