SLAM Course - WS13/14 by Cyrill Stachniss (4) 贝叶斯滤波器及相关模型

最新推荐文章于 2023-12-27 02:14:05 发布

游木木

最新推荐文章于 2023-12-27 02:14:05 发布

阅读量1.3k

点赞数

分类专栏： SLAM课程笔记文章标签：机器人贝叶斯滤波

本文链接：https://blog.csdn.net/yoouzx/article/details/53099354

版权

SLAM课程笔记专栏收录该内容

4 篇文章 0 订阅

订阅专栏

课件及相关资源下载：http://blog.csdn.net/yoouzx/article/details/53098176

贝叶斯滤波器

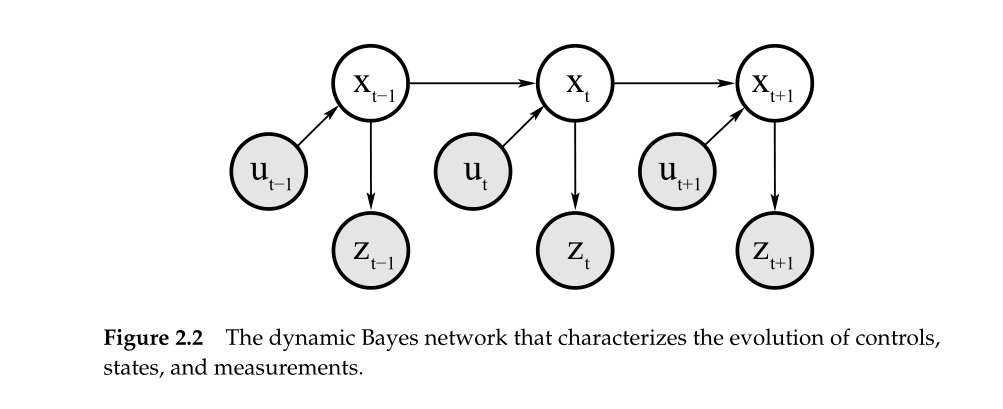
测量和控制输入

定义 $z_{1:t}$ 为不同时刻 $t$ 的环境测量值， $z_{1:t}$ 提供机器人周围的环境信息，可以是激光、图像数据等形式。定义 $u_{1:t}$ 为不同时刻 $t$ 的控制输入， $u_{1:t}$ 给出改变机器人状态的指令。由于传感器测量噪声和执行机构的误差（如齿轮间的不完全啮合，车轮大小不一致等），实际的测量和控制输入都是有噪声的，这引起了机器人状态的不确定性。定义 $x_{0：t}$ 为机器人不同时刻的状态， $x_{0}$ 表示机器人的初始状态。则 $z_{1:t}、u_{1:t}、x_{0：t}$ 之间的关系可以由下图表示。
状态、测量和控制转换图

预测方程和矫正方程的推导

贝叶斯滤波器的推导基于贝叶斯概率公式和马尔科夫假设。
1. 贝叶斯概率公式(后验概率)：

p (x | y) = p ( y | x ) p ( x ) p ( y ) = η p (y | x) p (x)

$p(x|y)=\frac{p(y|x) p(x)}{p(y)}=\eta p(y|x) p(x)$
当条件概率涉及到的变量比较多，上式分母就会变得比较复杂，为表示方便这里定义

η $\eta$ 为归一化参数。
相似的，我们可以考虑

p(x|y,z) $p(x|y,z)$ 的条件概率，这里可以看成在

z $z$ 发生的条件下，将概率

p(x|y) $p(x|y)$ 进行贝叶斯公式展开，代入二元贝叶斯公式得到：

p (x | y, z) = p ( y | x , z ) p ( x | z ) p ( y | z )

$p(x|y,z)=\frac {p(y|x,z) p(x|z)} {p(y|z)}$
2. 定义可信度：

b e l (x t) = p (x t | z 1 : t, u 1 : t)

$bel(x_{t})=p(x_{t}|z_{1:t},u_{1:t})$
3. 根据贝叶斯概率公式将上式展开（参考1.中三个变量贝叶斯公式推导）为：

b e l (x t) = p (x t | z 1 : t, u 1 : t) = η p ( z t | x t ， z 1 : t - 1 , u 1 : t ) ( 1 ) p ( x t | z 1 : t - 1 ， u 1 : t ) ( 2 )

$bel(x_{t})=p(x_{t}|z_{1:t},u_{1:t})\\=\eta \frac {p(z_{t}|x_{t}，z_{1:t-1},u_{1:t})}{(1)} \frac {p(x_t|z_{1:t-1}，u_{1:t})} {(2)}$
4. 根据马尔科夫假设进行简化
在probability robotics 这本书里，马尔科夫假设是全书的基本假设，所有的公式都是在这个假设基础行推导而来的，马尔科夫假设核心思想是：已知当前时刻的状态

xt $x_t$ ,不会影响过去和将来的状态。
对于3.公式（1）部分，

xt $x_t$ 可以根据之前

t−1 $t-1$ 个时刻的测量值

z1：t−1 $z_{1：t-1}$ 和t个时刻控制输入

u1:t $u_{1:t}$ 得到（参考1. 中状态转移图）。所以（1）部分简化为：

p (z t | x t, z 1 : t - 1, u 1 : t) = p (z t | x t)

$p(z_t|x_t,z_{1:t-1},u_{1:t})=p(z_t|x_t)$
对于公式（2）部分，在连续域进行展开：

p (x t | z 1 : t - 1 ， u 1 : t) = \int x t - 1 p (x t | x t - 1, z 1 : t - 1 ， u 1 : t) p (x t - 1 | z 1 : t - 1 ， u 1 : t) d x t - 1

$p(x_t|z_{1:t-1}，u_{1:t})=\int_{x_{t-1}} p(x_t|x_{t-1},z_{1:t-1}，u_{1:t})p(x_{t-1}|z_{1:t-1}，u_{1:t})d_{x_{t-1}}$
这一部分可以类比以下公式（B对应于上式

xt−1 $x_{t-1}$ ）：

p (A) = \int B p (A | B) p (B) d B (连 续 域) \sum B p (A | B) p (B) (离 散 域)

$p(A)=\int_B p(A|B)p(B)d_B(连续域)\\ \sum_Bp(A|B)p(B)(离散域)$
在马尔科夫假设前提下，已知将来的状态

ut $u_t$ 对估计

xt−1 $x_{t-1}$ 没用提供任何信息，所以：

p (x t | z 1 : t - 1 ， u 1 : t) = \int x t - 1 p (x t | x t - 1, z 1 : t - 1 ， u 1 : t) p (x t - 1 | z 1 : t - 1 ， u 1 : t) d x t - 1 = \int x t - 1 p (x t | x t - 1, z 1 : t - 1 ， u 1 : t) p (x t - 1 | z 1 : t - 1 ， u 1 : t - 1) d x t - 1 = \int x t - 1 p (x t | x t - 1, u t) b e l (x t - 1) d x t - 1

$p(x_t|z_{1:t-1}，u_{1:t})=\int_{x_{t-1}} p(x_t|x_{t-1},z_{1:t-1}，u_{1:t})p(x_{t-1}|z_{1:t-1}，u_{1:t})d_{x_{t-1}}\\=\int_{x_{t-1}} p(x_t|x_{t-1},z_{1:t-1}，u_{1:t})p(x_{t-1}|z_{1:t-1}，u_{1:t-1})d_{x_{t-1}}\\=\int_{x_{t-1}} p(x_t|x_{t-1},u_t) bel(x_{t-1})d_{x_{t-1}}$
5. 根据1-4推导，得到迭代的贝叶斯滤波公式：