一,说在前面的话
大概在半年前,看见一到信息竞赛题:在任意方格阵中设置障碍物,确定起始点后,求这两点之间路径。当时觉得蛮有意思的,但是没有时间去做,今天花了两个小时来实现它。据说有一个更高级的寻路算法叫做A*,可以启发式寻路。
此算法主要用于解迷宫和实现战棋游戏(SLG)的寻路。首先讲一讲我这个简易算法的思路:
我们先确定起始点,然后从起点出发,按一定顺序判断这个位置上下左右是否有可走的位置,如果发现有可走的位置,则递归进入该位置的判断。在递归的同时记录所走的路线。当发现某个位置无路可走,则删除路线的最后一个位置并返回上级位置进行判断。如此反复尝试最终找到路线。
说了这么多,就来讲解一下代码吧。
二,讲解部分
包含头文件(全部都是stl中的):
#include <map>
#include <vector>
#include <iostream>为几个冗长的类型重命名,用来使后来的代码更明了。
typedef unsigned int uint;
typedef std::vector<int> CRow;
//相当于把CLabyrinth定义成一个整型的二维数组
typedef std::vector<CRow> CLabyrinth;class CPoint
{
public:
int col; //列
int row; //行
public:
//构造函数,接受行和列的初始化
CPoint(int c = 0, int r = 0)
: col(c)
, row(r)
{
return;
}
//赋值操作
CPoint& operator=(const CPoint& pt)
{
col = pt.col;
row = pt.row;
return *this;
}
//比较操作
bool operator==(const CPoint& pt)
{
return col == pt.col && row == pt.row;
}
//判断该位置是否合法
bool allRight()
{
return col >= 0 && row >= 0;
}
};
typedef std::vector<CPoint> CRoute;然后到了核心类类型CLabyrinthAI
{
protected:
//装有迷宫数据的二维数组
CLabyrinth m_xLabyrinth;
//起点位置
CPoint m_ptBeginning;
//终点位置
CPoint m_ptEnding;
//记录路线的数组
CRoute m_vRoute;
public:
//枚举表示起点、终点的值
enum{Beginning = -1, Ending = -2};
//枚举表示障碍物与可走区的值
enum{CanntGo = 0, CanGo = 1};
//枚举是否找到终点
enum{FoundEnding = 0, NotFoundEnding = 1};
protected:
//判断某个位置是否已在路线数组中,用于别走重复的路
bool isRepeat(const CPoint& pt)
{
bool bRes = false;
CRoute::iterator it = m_vRoute.begin();
for(; it != m_vRoute.end(); it++){
CPoint pt0 = *it;
if(pt0 == pt){
bRes = true;
break;
}
}
return bRes;
}
//将某一位置加入路线数组
void advance(const CPoint& ptTo)
{
m_vRoute.push_back(ptTo);
}
//将路线数组最后一个位置弹出
void back()
{
m_vRoute.pop_back();
}
//判断某一位置是否是起点
bool isBeginning(const CPoint& pt)
{
return m_ptBeginning == pt;
}
//判断某一位置是否是终点
bool isEnding(const CPoint& pt)
{
return m_ptEnding == pt;
}
/*-----------------核心算法------------------------*/
//判断某一位置是否可以向上移动
CPoint canUp(const CPoint& ptCurrent) //接受当前位置
{
CPoint ptRes = CPoint(-1, -1);
int col = ptCurrent.col;
int row = ptCurrent.row;
if(row > 0){
CPoint ptNext = CPoint(col, row - 1); //上移后位置
//检查上移后位置是否已经走过,以免寻路过程中绕圈子进入死循环
if(!isRepeat(ptNext)){
//获得迷宫二维数组中上移后位置的属性(起点、终点、可走、障碍)
int nAttr = m_xLabyrinth[ptNext.row][ptNext.col];
//如果上移后位置为可走或到达终点,则设定返回值为上移后的位置
if(nAttr == CanGo || nAttr == Ending){
ptRes = ptNext;
}
}
}
return ptRes; //如果上移后位置不可走则返回非法的位置
}
//以下判断某一位置可否移动的原理大致与上相同,就不多说了
//判断某一位置是否可以向下移动
CPoint canDown(const CPoint& ptCurrent)
{
CPoint ptRes = CPoint(-1, -1);
int col = ptCurrent.col;
int row = ptCurrent.row;
if(row < m_xLabyrinth.size() - 1){
CPoint ptNext = CPoint(col, row + 1);
if(!isRepeat(ptNext)){
int nAttr = m_xLabyrinth[ptNext.row][ptNext.col];
if(nAttr == CanGo || nAttr == Ending){
ptRes = ptNext;
}
}
}
return ptRes;
}
//判断某一位置是否可以向左移动
CPoint canLeft(const CPoint& ptCurrent)
{
CPoint ptRes = CPoint(-1, -1);
int col = ptCurrent.col;
int row = ptCurrent.row;
if(col > 0){
CPoint ptNext = CPoint(col - 1, row);
if(!isRepeat(ptNext)){
int nAttr = m_xLabyrinth[ptNext.row][ptNext.col];
if(nAttr == CanGo || nAttr == Ending){
ptRes = ptNext;
}
}
}
return ptRes;
}
//判断某一位置是否可以向右移动
CPoint canRight(const CPoint& ptCurrent)
{
CPoint ptRes = CPoint(-1, -1);
int col = ptCurrent.col;
int row = ptCurrent.row;
if(col < m_xLabyrinth[0].size() - 1){
CPoint ptNext = CPoint(col + 1, row);
if(!isRepeat(ptNext)){
int nAttr = m_xLabyrinth[ptNext.row][ptNext.col];
if(nAttr == CanGo || nAttr == Ending){
ptRes = ptNext;
}
}
}
return ptRes;
}
/*
*判断某一位置是否可以向四周移动,如果判断到某一位置可以移动,则递归进入该位置判断。
*如果该位置没有任何位置可移动,则返会上级位置并且调用back函数。如果走到终点,
*则立刻返回枚举值FoundEnding,上级位置检查到返回值为FoundEnding,也直接返回。
*/
int findRoute(const CPoint& ptCurrent)
{
int nRes = NotFoundEnding; //默认返回值为没有找到终点
CPoint ptNext = CPoint(-1, -1);
advance(ptCurrent); //将当前位置加入路线数组
//判断当前位置是否是终点,如果是终点则不进行下面的判断,将返回值设置为找到终点
if(isEnding(ptCurrent)){
nRes = FoundEnding;
}else{ //按上左下右的顺序判断有无可走路径
//尝试向上
ptNext = canUp(ptCurrent); //获取向上走后的位置
//判断向上走后的位置是否是合法位置,若不合法,则表明上走到了迷宫的边缘,或者上面没有可走路径
if(ptNext.allRight()){
//上述判断成功,则将向上移动后的位置传入给自己,进行递归。当该函数退出,查看返回值是否为找到终点。若找到终点则立刻返回FoundEnding
if(findRoute(ptNext) == FoundEnding){
nRes = FoundEnding;
return nRes;
}
}
//下列尝试四周位置是否可走的代码与上述大体相同,就不多说了
//尝试向左
ptNext = canLeft(ptCurrent);
if(ptNext.allRight()){
if(findRoute(ptNext) == FoundEnding){
nRes = FoundEnding;
return nRes;
}
}
//尝试向下
ptNext = canDown(ptCurrent);
if(ptNext.allRight()){
if(findRoute(ptNext) == FoundEnding){
nRes = FoundEnding;
return nRes;
}
}
//尝试向右
ptNext = canRight(ptCurrent);
if(ptNext.allRight()){
if(findRoute(ptNext) == FoundEnding){
nRes = FoundEnding;
return nRes;
}
}
}
//检测是否到达终点,若没有到达终点,则立刻从路线表中删除该位置
if(nRes != FoundEnding){
back();
}
return nRes;
}
/*-----------------核心算法------------------------*/
public:
//构造函数
CLabyrinthAI()
{
return;
}
//带有初始化迷宫数组构造函数
CLabyrinthAI(const CLabyrinth& vLabyrinth)
{
m_xLabyrinth = vLabyrinth;
getBeginning();
getEnding();
}
//初始化迷宫数组
void setLabyrinth(const CLabyrinth& vLabyrinth)
{
m_xLabyrinth = vLabyrinth;
}
//查找起点
void getBeginning()
{
uint nRow = 0;
for(; nRow < m_xLabyrinth.size(); nRow++){
CRow xRow = m_xLabyrinth[nRow];
uint nCol = 0;
for(; nCol < xRow.size(); nCol++){
int n = xRow[nCol];
if(n == Beginning){
m_ptBeginning = CPoint(nCol, nRow);
break;
}
}
}
}
//查找终点
void getEnding()
{
uint nRow = 0;
for(; nRow < m_xLabyrinth.size(); nRow++){
CRow xRow = m_xLabyrinth[nRow];
uint nCol = 0;
for(; nCol < xRow.size(); nCol++){
int n = xRow[nCol];
if(n == Ending){
m_ptEnding = CPoint(nCol, nRow);
break;
}
}
}
}
//调用核心算法函数,输出获得的路线
void AI()
{
findRoute(m_ptBeginning);
if(!m_vRoute.empty()){
CRoute::iterator it = m_vRoute.begin();
for(; it != m_vRoute.end(); it++){
CPoint pt = *it;
std::cout << "(" << pt.row << ", " << pt.col << ")";
if(it != m_vRoute.end() - 1){
std::cout << "->";
}else{
std::cout << std::endl;
}
}
}else{
//如果没有找到路线到达终点
std::cout << "Sorry cannot file any ways to get ending." << std::endl;
}
}
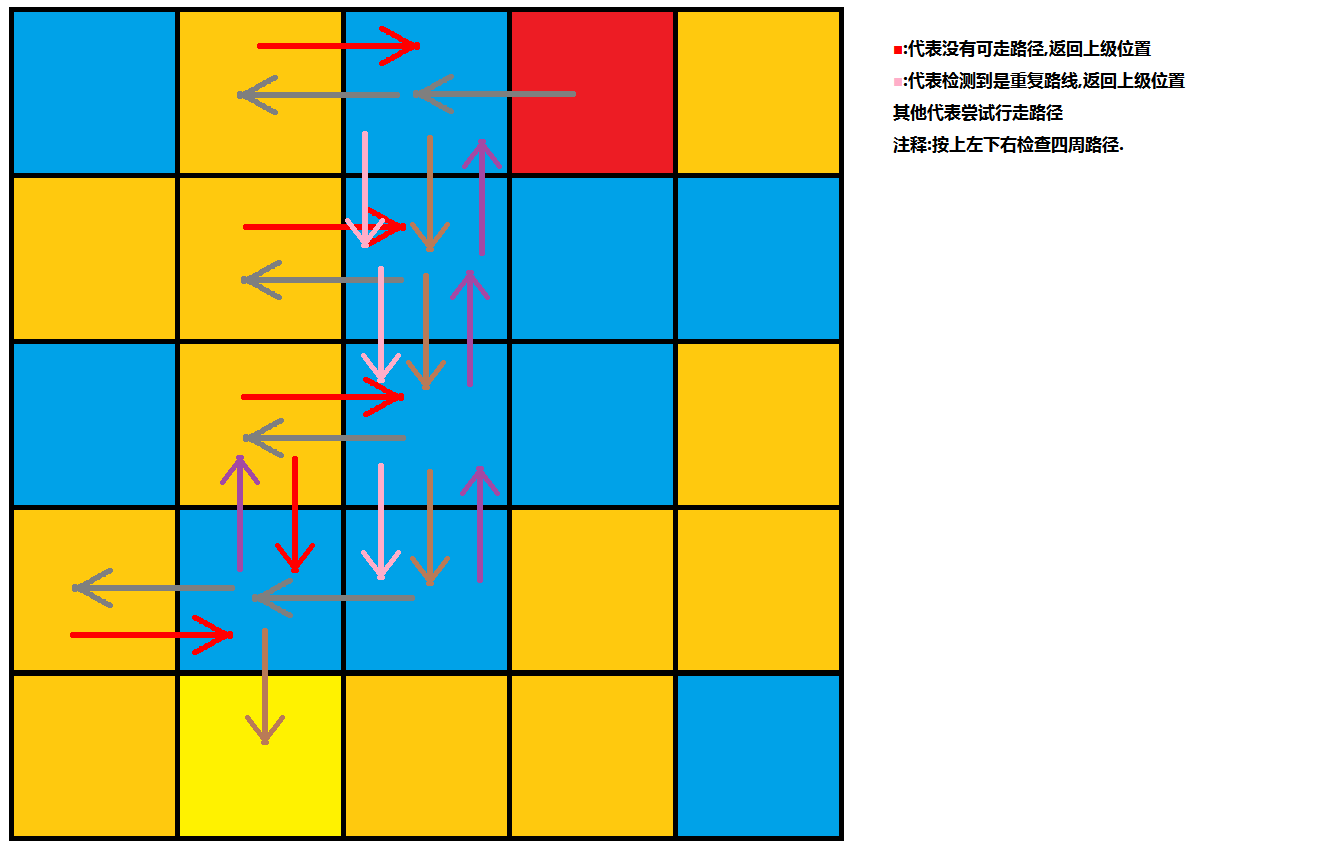
};如果上述过程把你搅晕了,那就用图来为你解答吧。
然后来到main函数
//用VC 6.0貌似不需要给main传参数,那我就偷一下懒
int main()
{
//定义迷宫数组,定义成C风格的二维数组方便查看
int vLabyrinthArray[][4] = {
{1,0,-1,1}
, {1,0,0,1}
, {0,0,1,1}
, {0,1,1,0}
, {0,1,1,1}
, {-2,1,0,0}
};
//以下代码为将C风格的二维数组导入成C++风格的二维数组
int nRowNum = sizeof(vLabyrinthArray) / sizeof(vLabyrinthArray[0]);
int nColNum = sizeof(vLabyrinthArray[0]) / sizeof(int);
CLabyrinth vLabyrinth;
for(int row = 0; row < nRowNum; row++){
CRow xRow;
for(int col = 0; col < nColNum; col++){
int n = vLabyrinthArray[row][col];
xRow.push_back(n);
}
vLabyrinth.push_back(xRow);
}
//实例化CLabyrinthAI
CLabyrinthAI xAI(vLabyrinth);
//打出路线
xAI.AI();
//使程序暂停,方便查看数据
system("Pause");
return 0;
}以上代码同样加了注释,相信了解C++的同学都能看懂。
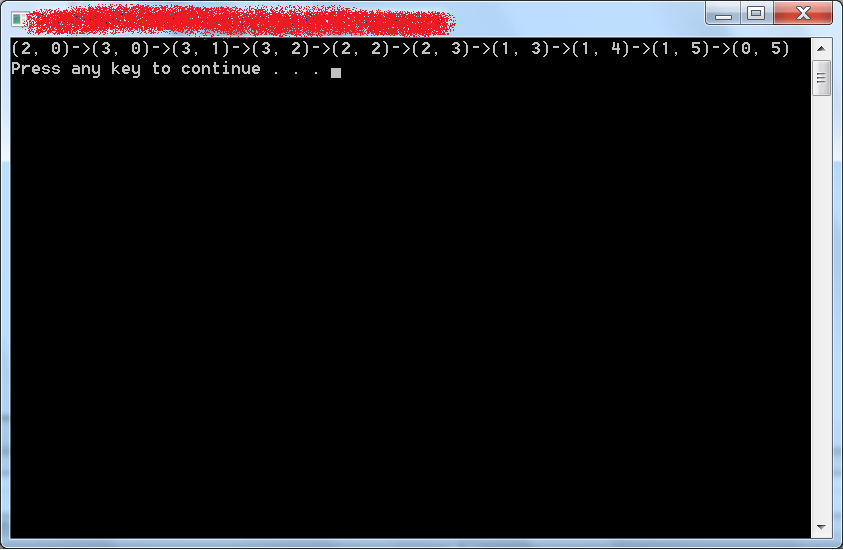
运行截图:
(Dos的,有点丑…… )
)
三,Javascript版
顺便我也把C++版的移植到了Javascript上,代码如下:
function CLabyrinthAI(){
var s = this;
s.m_xLabyrinth = new Array(new Array());
s.m_ptBeginning = {};
s.m_ptEnding = {};
s.m_vRoute = new Array();
s.Beginning = -1;
s.Ending = -2;
s.CannotGo = 0;
s.CanGo = 1;
s.FoundEnding = 0;
s.NotFoundEnding = 1;
}
CLabyrinthAI.prototype.initAI = function(){
var s = this;
s.getBeginning();
s.getEnding();
}
CLabyrinthAI.prototype.isRepeat = function(pt){
var s = this;
var bRes = false;
for(var n = 0; n < s.m_vRoute.length; n++){
var pt0 = s.m_vRoute[n];
if(pt0.col == pt.col && pt0.row == pt.row){
bRes = true;
break;
}
}
return bRes;
};
CLabyrinthAI.prototype.advance = function(ptTo){
this.m_vRoute.push(ptTo);
};
CLabyrinthAI.prototype.back = function(){
this.m_vRoute.splice(this.m_vRoute.length-1,1);
};
CLabyrinthAI.prototype.isBeginning = function(pt){
if(this.m_ptBeginning.col == pt.col && this.m_ptBeginning.row == pt.row){
return true;
}else{
return false;
}
};
CLabyrinthAI.prototype.isEnding = function(pt){
if(this.m_ptEnding.col == pt.col && this.m_ptEnding.row == pt.row){
return true;
}else{
return false;
}
};
CLabyrinthAI.prototype.canUp = function(ptCurrent){
var s = this;
var ptRes = {col:-1,row:-1};
var col = ptCurrent.col;
var row = ptCurrent.row;
if(row > 0){
var ptNext = {col:col,row:row - 1};
if(!s.isRepeat(ptNext)){
var nAttr = s.m_xLabyrinth[ptNext.row][ptNext.col];
if(nAttr == s.CanGo || nAttr == s.Ending){
ptRes = ptNext;
}
}
}
return ptRes;
};
CLabyrinthAI.prototype.canDown = function(ptCurrent){
var s = this;
var ptRes = {col:-1,row:-1};
var col = ptCurrent.col;
var row = ptCurrent.row;
if(row < s.m_xLabyrinth.length - 1){
var ptNext = {col:col,row:row + 1};
if(!s.isRepeat(ptNext)){
var nAttr = s.m_xLabyrinth[ptNext.row][ptNext.col];
if(nAttr == s.CanGo || nAttr == s.Ending){
ptRes = ptNext;
}
}
}
return ptRes;
};
CLabyrinthAI.prototype.canLeft = function(ptCurrent){
var s = this;
var ptRes = {col:-1,row:-1};
var col = ptCurrent.col;
var row = ptCurrent.row;
if(col > 0){
var ptNext = {col:col-1,row:row};
if(!s.isRepeat(ptNext)){
var nAttr = s.m_xLabyrinth[ptNext.row][ptNext.col];
if(nAttr == s.CanGo || nAttr == s.Ending){
ptRes = ptNext;
}
}
}
return ptRes;
};
CLabyrinthAI.prototype.canRight = function(ptCurrent){
var s = this;
var ptRes = {col:-1,row:-1};
var col = ptCurrent.col;
var row = ptCurrent.row;
if(col < s.m_xLabyrinth[0].length - 1){
var ptNext = {col:col+1,row:row};
if(!s.isRepeat(ptNext)){
var nAttr = s.m_xLabyrinth[ptNext.row][ptNext.col];
if(nAttr == s.CanGo || nAttr == s.Ending){
ptRes = ptNext;
}
}
}
return ptRes;
};
CLabyrinthAI.prototype.allRight = function(p){
if(p.col >= 0 && p.row >= 0){
return true;
}else{
return false;
}
};
CLabyrinthAI.prototype.findRoute = function(ptCurrent){
var s = this;
var nRes = s.NotFoundEnding;
var ptNext = {col:-1,row:-1};
s.advance(ptCurrent);
if(s.isEnding(ptCurrent)){
nRes = s.FoundEnding;
}else{
ptNext = s.canUp(ptCurrent);
if(s.allRight(ptNext)){
if(s.findRoute(ptNext) == s.FoundEnding){
nRes = s.FoundEnding;
return nRes;
}
}
ptNext = s.canLeft(ptCurrent);
if(s.allRight(ptNext)){
if(s.findRoute(ptNext) == s.FoundEnding){
nRes = s.FoundEnding;
return nRes;
}
}
ptNext = s.canDown(ptCurrent);
if(s.allRight(ptNext)){
if(s.findRoute(ptNext) == s.FoundEnding){
nRes = s.FoundEnding;
return nRes;
}
}
ptNext = s.canRight(ptCurrent);
if(s.allRight(ptNext)){
if(s.findRoute(ptNext) == s.FoundEnding){
nRes = s.FoundEnding;
return nRes;
}
}
}
if(nRes != s.FoundEnding){
s.back();
}
return nRes;
};
CLabyrinthAI.prototype.getBeginning = function(){
var s = this;
for(var nRow = 0; nRow < s.m_xLabyrinth.length; nRow++){
var xRow = s.m_xLabyrinth[nRow];
for(var nCol = 0; nCol < xRow.length; nCol++){
var n = xRow[nCol];
if(n == s.Beginning){
s.m_ptBeginning = {col:nCol,row:nRow};
break;
}
}
}
};
CLabyrinthAI.prototype.getEnding = function(){
var s = this;
for(var nRow = 0; nRow < s.m_xLabyrinth.length; nRow++){
var xRow = s.m_xLabyrinth[nRow];
for(var nCol = 0; nCol < xRow.length; nCol++){
var n = xRow[nCol];
if(n == s.Ending){
s.m_ptEnding = {col:nCol,row:nRow};
break;
}
}
}
};
CLabyrinthAI.prototype.AI = function(data){
var s = this;
s.m_xLabyrinth = data;
s.initAI();
s.findRoute(s.m_ptBeginning);
return s.m_vRoute;
};
虽然这套算法是研究出来了,但是还不能判断是否为最近路线,因此有待更新。不过以现在的算法,开发一个SLG应该不是问题了。
※感谢我的哥哥与我一起讨论其中的原理。
源代码下载:
http://files.cnblogs.com/yorhom/findRoute.rar
谢谢大家阅读本文,支持就是最大的鼓励。
----------------------------------------------------------------
欢迎大家转载我的文章。
转载请注明:转自Yorhom's Game Box
http://blog.csdn.net/yorhomwang
欢迎继续关注我的博客
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








