马尔科夫链表示state的链式关系,下一个state只跟上一个state有关。
吉布斯采样通过采样条件概率分布得到的样本点,近似估计概率分布
P(z)
。PageRank通过节点间的连接,估计节点的重要程度
r
。吉布斯采样中,state代表不同的样本点,state的分布就是state代表不同节点的分数,state的分布就是要求的
r
。不论吉布斯采样还是PageRank,state的分布本质上都是马尔科夫链,而最后都希望state的分布是独一并且稳定的。
Markov Chain
介绍
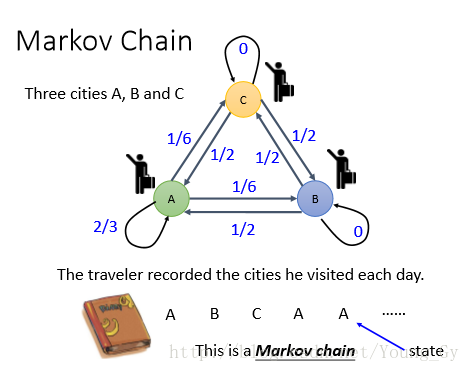
上图表示了一个典型的马尔科夫链,每个城市A、B、C代表不同的state。该图描述了不同state间的转移变化关系。并且下一个时间的state只和上一个时间的state有关。
稳定态
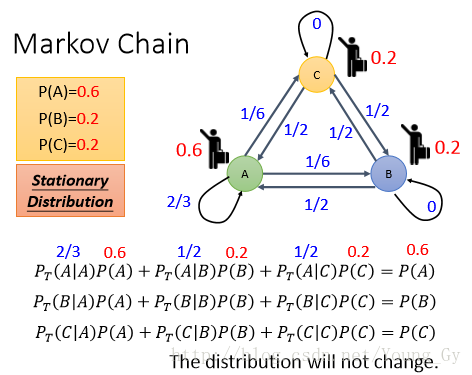
想象上述的马尔科夫链,state不停的变化,我们可以求出不同state的概率,也就是state的概率分布。
最简单的办法是列出不同state的概率公式,然后解线性方程组求解,如下:
可是,单一稳定的state不一定存在,例如下面两种情况:
Spider trap,a⇔b ,相当于状态被困在某区域(多个状态)。Dead End, a⇒b ,相当于状态被困在单个状态中。那么,什么情况下才有单一稳定的
state的存在呢?单一稳定的
state分布的存在的充分条件是:对于任意两个states1,s2 ,它们之间的状态转移概率不为0。也就是 p(s1|s2)>0 。也就是说,state间(包含自身)都有连接,这样的话便存在单一稳定的state分布。Gibbs Sampling
介绍
Gibbs Sampling遇到的问题是:在已知 P(zi|z1,...,zi−1,zi+1,...zN) 分布的情况下,求变量 P(z)(z=z1,...,zN) 的分布。
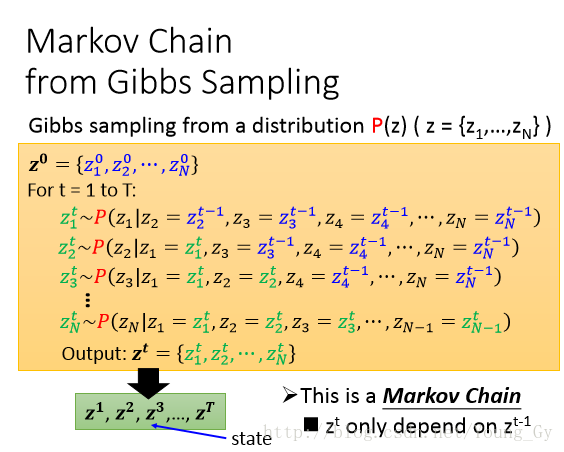
Gibbs Sampling的解决办法是:设置外循环 t ,遍历采样点数;设置内循环
k ,遍历特征数,对于每一个特征值 ztk ,根据分布 ztk∼P(zk=ztk|z1=zt1,z2=zt2,...) 采样 ztk 。最后,根据 z1,z2,z3,... 得到 P(z)(z=z1,...,zN) 的分布。Gibbs Sampling与Markov
吉布斯采样的数据 z1,z2,z3,... 相当于马尔科夫链中不同的
state(因为 zt 只和 zt−1 有关)。如果马尔科夫链存在单一且稳定的状态分布,那么就可以通过采样求出 P(z)(z=z1,...,zN) 。下面,分两个步骤证明:
- Gibbs Sampling存在单一且稳定的状态分布。
- Gibbs Sampling单一且稳定的状态分布就是 P(z) 。
Gibbs Sampling中条件概率没有0值确保了Gibbs Sampling存在单一且稳定的状态分布。
根据概率公式,可推导Gibbs Sampling单一且稳定的状态分布就是 P(z) 。
Page Rank
介绍
Page Rank的哲学是:一个点的重要性跟这个点的in-link有关,不同的in-link权重不一样,score越大的节点对应的in-link也就越重要。
令节点的score向量为 r ,节点的邻接矩阵为M 。那么, r 和M 的关系可写作:
r=Mr示例如下:
这个例子中,可以把矩阵 M 和向量
r 相乘当做 M 的列以向量r 为权重进行线性组合,矩阵 M 同一列的不同行代表该节点向其他节点的分发连接。这样理解起来就比较清晰了。r 的求解可以使用特征值-特征向量分解,最大特征值对应的特征向量即是 r 。稳定性
r 的值在满足特定情况下才是单一且稳定的。实际计算Page Rank中,需要增加一个条件:每个节点都有 1N 的概率变换到任何其他节点状态。
原来的式子是:
r=Mr考虑稳定性后的式子是:
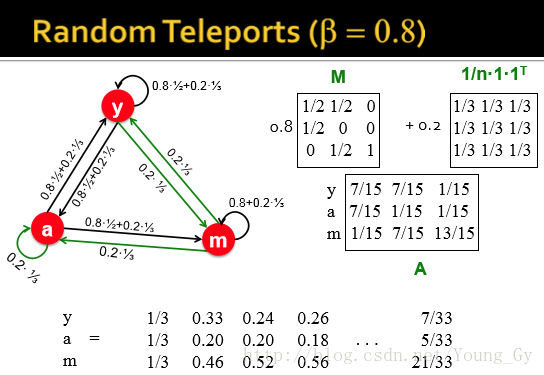
Ar=βM+(1−β)1N11T=Ar示例如下:
稀疏计算
在上面的计算公式中,矩阵 A 是稠密的,空间复杂度是
O(N2) ,占得空间很大。因此,改进计算如下:
Arr=βM+(1−β)1N11T=Ar=βMr+1−βN























 2496
2496











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








