白皮书 | 分布式存储发展白皮书（2023）

12月1日，在2023云原生产业大会上，中国信通院云大所联合华为、戴尔科技、IBM等分布式存储产业方阵成员单位共同发布《分布式存储发展白皮书（2023年）》

一、数据智能的需求

（一）大模型训练需要海量的非结构化数据，对数据存储、流动的效率提出了更高的需求。

（二）数据流动作为算力互联互通的关键组成部分，是释放算力资源价值的基础，也是解决数算协同问题的关键环节。

二、产业解析

（一）筑稳数据底座，分布式存储市场呈现稳健增长。

2022年，中国的分布式存储市场规模预计为 205亿元，年复合增长率达到15%。其中，软硬一体的存储解决方案占据了市场的91.3%，主要是满足 AI 大型模型和大数据湖等场景下的非结构化数据需求。

（二）产业生态图景，产业生态紧密合作

从分布式存储全产业链发展的角度来看，生态产业均均呈现规模增长，产品形态及服务类型呈现多元化态势。

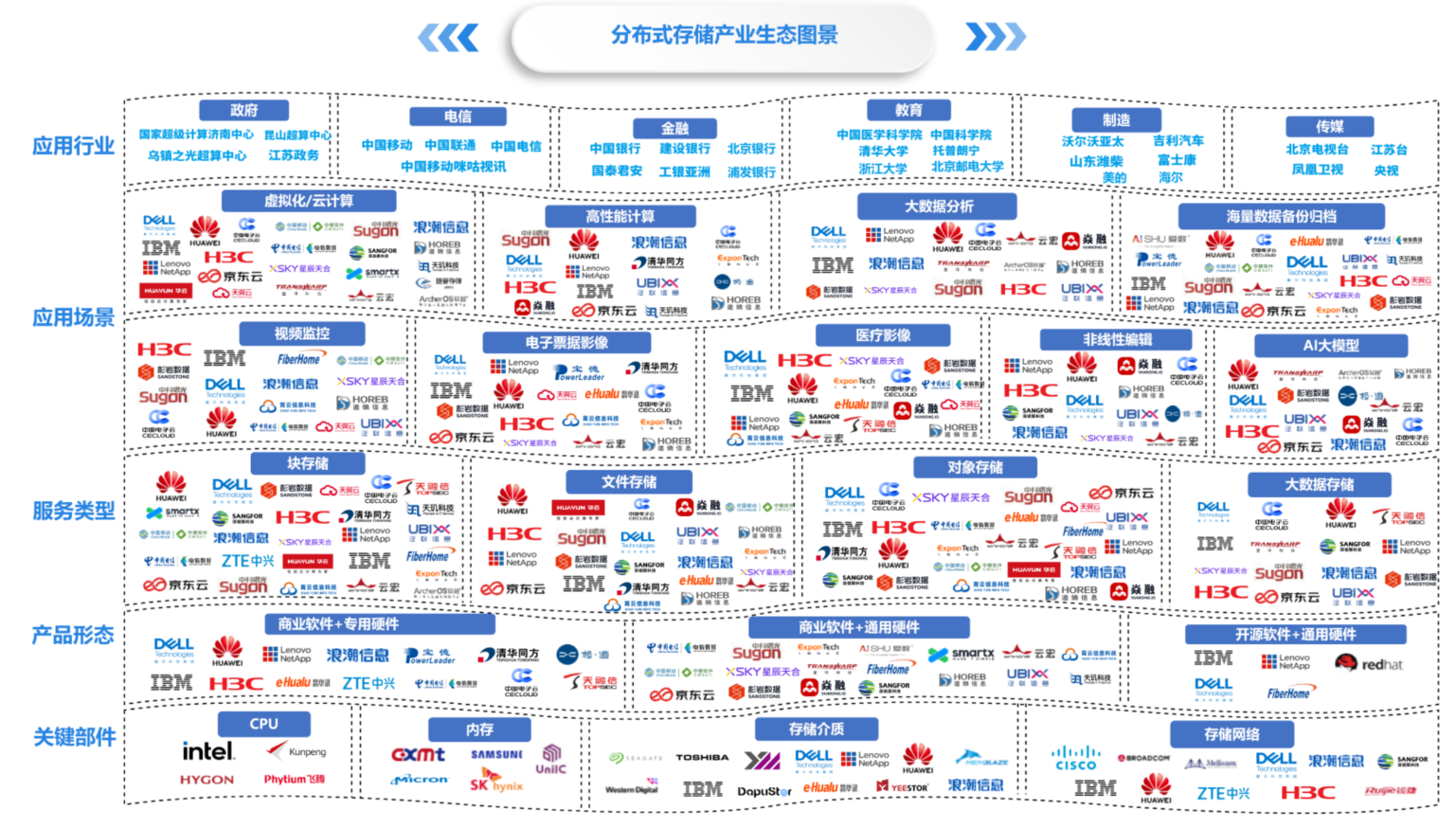
（三） 介质协议加速升级，全闪与融合形态快速发展

得益于闪存性能、高速无损 RDMA 网络、压缩软件栈等全闪存化设计，分布式全闪存储作为一种新的存储产品形态，提供稳定的亚毫秒级访问性能。

分布式存储已经发展出分布式融合存储新形态，通过一套分布式存储系统支持多种协议同时提供服务，并实现协议互通，减少数据搬迁和重复存储，提升 35%的数据处理效率，降低约 20%能耗。

三、场景解读

分布式存储的应用场景日益丰富，本白皮书将重点探讨其中的新兴应用场景及典型应用场景的发展趋势。涵盖的场景包括AI大模型、大数据湖仓一体、数字化病理、生物信息分析、量化交易、边缘计算以及数据网络。

场景	特征	分布式存储优势
AI大模型	大数据量、数据并行处理、数据格式多样、海量小文件、高可靠高可用	海量存储空间及在线扩展、海量存储空间、协议互通的高效数据流动、海量小文件性能支持。
大数据湖仓一体	事务支持、开放数据格式、存储与计算分离、支持多种工作负载、BI支持	统一数据存储层、统一元数据层、缓存加速、统一计算调度
数字化病理	切片文件大、数据量大、数据保存久、数据管理难	病理图片二次压缩、数据分级存储、实现海量切片并发调阅、冷数据存储介质创新、多协议互通
生物信息分析	大数据量、高带宽低时延、高可靠、需适配GPU等高并发算力集群	海量数据支持、性能适配业务需求、数据全生命周期管理
量化交易	基础量化数据规模大、量化交易依托“AI+机器学习”成为行业主流、数据类型多、信噪比低	海量数据支持、弹性扩展、GPU存储直通、统一命名空间
边缘计算	超低时延、数据安全、灵活性与可扩展性、高可靠性、云边协同、边缘智能	数据长期低成本存储、快速检索、多协议互通、支持大数据分析、保障数据安全；
数据网络	跨地域、跨架构、跨服务商、大数据量	存储层构建数据跨域、跨云流动能力；面向多云构建统一数据底座，扩大数据共享应用；构建全局文件系统，形成数据互联网络；

四、技术透视

（一） 架构方面，向融合负载、更高密度、更快网络发展；

（二） 功能方面，向场景化无损压缩、多活容灾发展；

（三） 硬件方面，向全闪存化、高效节能发展；

（四） 生态方面，向云存开放对接、存储直通发展；

五、共建共赢

（一）生态上，建设云存开放对接、算力互联互通生态；

（二）产业上，推动分布式存储创新，构建 AI 数据引擎；

（三） 标准上，完善标准及评估体系，促进产业健康发展；

下载链接：

链接：https://pan.baidu.com/s/1Urcb1VCrcqMkb4UgTkHvcQ?pwd=pqcu

关注博主公众号，获取最新技术博文：

谢谢您的关注