python解常微分方程

一、sympy.dsolve

首先，感觉最科学的是用sympy的dsolve解常微分方程，直接贴代码

import sympy as sy

def differential_equation(x,f):
    return sy.diff(f(x),x,2)+f(x)#f(x)''+f(x)=0 二阶常系数齐次微分方程
x=sy.symbols('x')#约定变量
f=sy.Function('f')#约定函数
print(sy.dsolve(differential_equation(x,f),f(x)))#打印
sy.pprint(sy.dsolve(differential_equation(x,f),f(x)))#漂亮的打印

输出：

Eq(f(x), C1*sin(x) + C2*cos(x))
f(x) = C₁⋅sin(x) + C₂⋅cos(x)

如果学过二阶常系数齐次解法的话，很容易知道这是对的，你也可以试下更简单的微分方程验证。

二、scipy.integrate.odeint

这个用起来就比较麻烦了，不过用于画图还是很棒的。先看一个一阶微分方程的例子。

import numpy as np
from scipy.integrate import odeint
#一阶微分方程的例子
def diff_equation(y,x):
    #dy/dx=y，其实手工解的话，很容易知道，y=Cexp(x)
    return np.array(y)#微分方程格式，左边一定是dy/dx,返回右边
x=np.linspace(0,1,num=100)#初始点是0
result=odeint(diff_equation,1,x)#中间那个是y0初值，即x=0时y=1
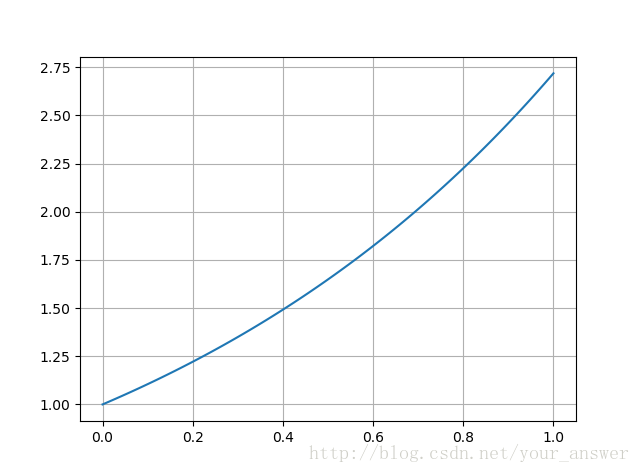
plt.plot(x,result[:,0])#result整个矩阵的第一列
plt.grid()#网格
plt.show()#这是y=exp(x)的图像

输出：

然而二阶的话，就有点麻烦了。

import numpy as np
from scipy.integrate import odeint
#二阶微分方程
def diff_equation(y_list,x):
    #y''+y=0 二阶的话，要换成两个一阶微分方程的方程组
    #设y'=z
    #那么z'=y''=-y
    #手工解也很容易知道是 y=C1sin(x)+C2cos(x)
    y,z=y_list
    return np.array([z,-y])
x=np.linspace(0,np.pi*2,num=100)
y0=[1,1]#y(0)=1,y'(0)=1
result=odeint(diff_equation,y0,x)
plt.plot(x,result[:,0],label='y')#y的图像，y=cos(x)+sin(x)
plt.plot(x,result[:,1],label='z')#z的图像，也就是y'的图像，z=-sin(x)+cos(x)
plt.legend()
plt.grid()
plt.show()

输出：

对了，想知道更详细的参数就看官网吧：

1、http://docs.sympy.org/dev/modules/solvers/ode.html

2、https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html