Dr_Can自动控制理论学习——根轨迹

ysh12345678gok

已于 2023-09-23 23:20:16 修改

阅读量92

点赞数

文章标签：学习

于 2023-09-23 21:31:02 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/ysh12345678gok/article/details/133217332

版权

本文部分素材来自Dr_Can的B站教程，请支持原作者。DR_CAN的个人空间-DR_CAN个人主页-哔哩哔哩视频 (bilibili.com)

1. 二阶系统标准形式

$\ddot{y}(t)+2\zeta\omega_n\dot{y}(t)+{\omega_n}^2y(t)={\omega_n}^2u(t)$

$U(s)$ 为常数，可知 $X(s)$ 为

$X(S)=\frac{1}{s^2+2\zeta\omega_ns+{\omega_n}^2}$

另

$s^2+2\zeta\omega_ns+{\omega_n}^2=0$

可知根为

$S=\frac{-2\zeta w_{n}\pm\sqrt{4\zeta^{2}w_{n}^{2}-4w_{n}^{2}}}{2}$

化简为

$S=-\zeta w_{n}\pm w_{n}\sqrt{\zeta^{2}-1}$

可知根为

$P_1=-\zeta w_{n}+ w_{n}\sqrt{\zeta^{2}-1}$ 和 $P_2=-\zeta w_{n}- w_{n}\sqrt{\zeta^{2}-1}$

将上式分解可得

$X(s)=\frac{1}{(s-p_{1})(s-p_{2})}=\frac{C_1}{s-p_{1}}+\frac{C_2}{s-p_{2}}$

转换为时域形式

$X(t)=C_{1}e^{ p_{1}t}+C_{2} e^{p_{2}t}$

当 $\zeta>1$ 时，P1和P2<0,根位于负实轴上，根越远离0收敛越快，但是最终收敛的速度取决于离0最近的根。

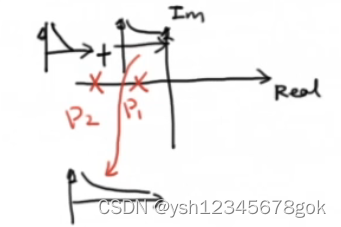
当 $\zeta=0$ 时

$P_1= w_{n}i$ 和 $P_2= -w_{n}i$

可知

$X{(s)}=\frac{1}{(s-iw_{n})(s+iw_{n})}=\frac{1}{s^{2}+w_{n}^{2}}=\frac{1}{w_{n}} \frac{w_{n}}{s^{2}+w_{n}}$

由拉普拉斯反变换 $L\left[\sin at\right]=\frac a{s^2+a^2}$ 可知

$X{(t)}=\frac{1}{w_{n}}\sin (w_{n}t)$

所体现出两个根在虚轴两侧，一直震荡不会收敛。

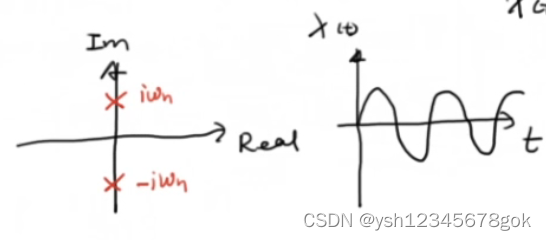
当 $\zeta<0$ 时

$X(s)=\frac{1}{(s+\zeta w_{n}- iw_{n}\sqrt{\zeta^{2}-1})(s+\zeta w_{n}+ iw_{n}\sqrt{\zeta^{2}-1})}=\frac{1}{(s+\zeta w_{n})^2+w_{n}^{2}(\zeta^{2}-1)}$

定义阻尼固有频率

$w_d=w_{n}\sqrt{\zeta^{2}-1}$

此时有

$X(s)=\frac{1}{(s+\zeta w_{n})^2+w_{d}^{2}}$

$X{(s)}=\frac{1}{(s+\zeta w_{n})^{2}+w_{d}^{2}}=\frac{1}{w_{d}} \frac{w_{d}}{(s+\zeta w_{n})^{2}+w_{d}}$

常用拉氏变换表 - YKR - 博客园 (cnblogs.com)

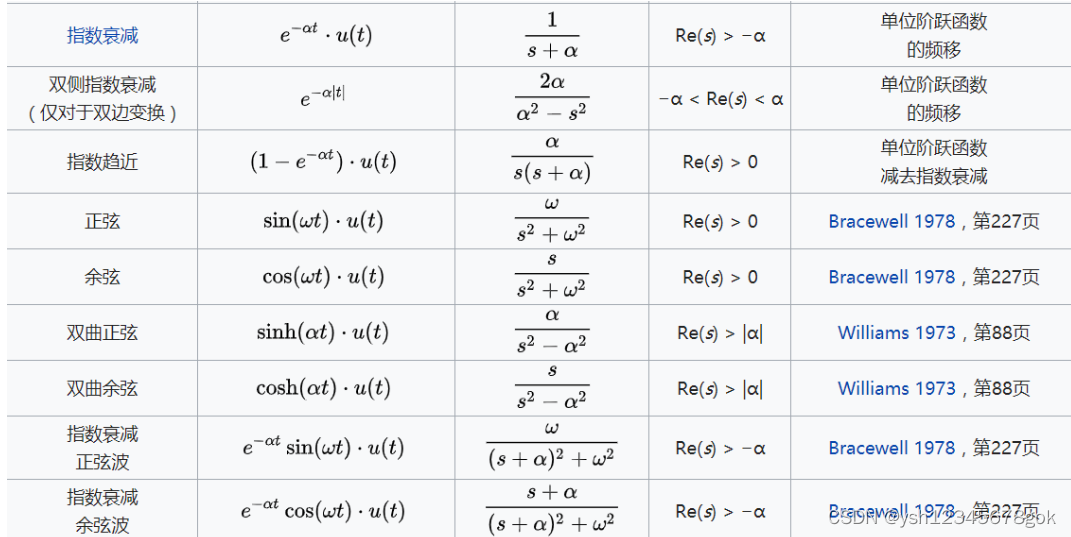
符合指数衰减正弦波

$X{(s)}=\frac{1}{w_{d}}e^{-\zeta w_{n}t}\sin (w_{d}t)$

若将根向左移动，那么系统的震荡频率不变，但是收敛的速度会变快。

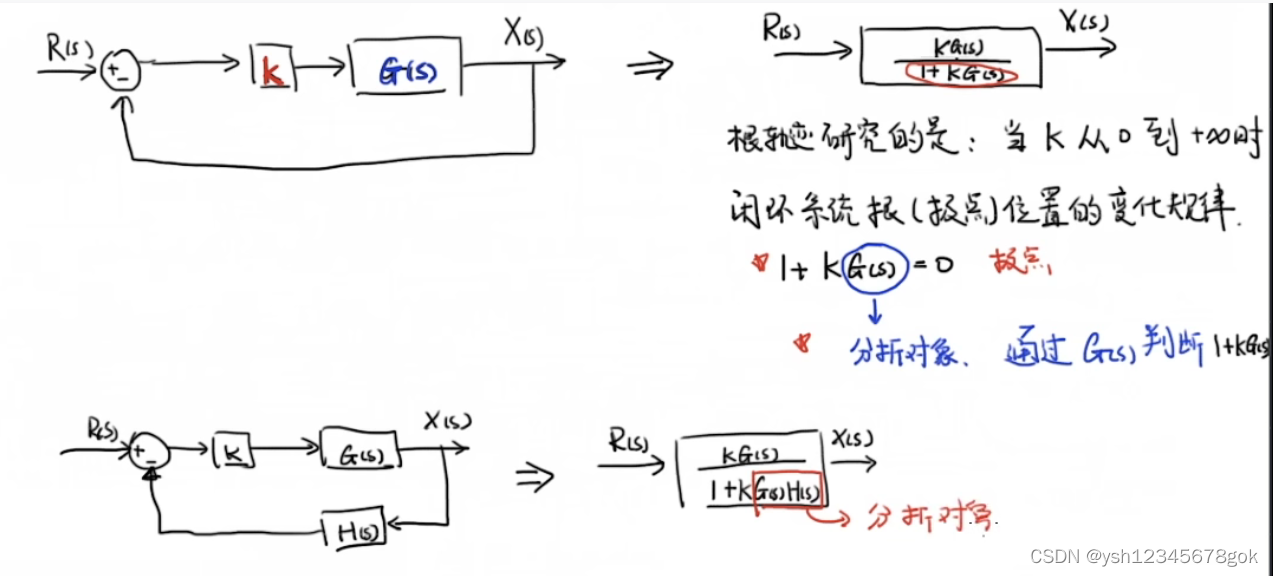
分析根轨迹时基于开环传递函数极点分析，通过G(s)判断1+G(s)=0，若存在H(s),那么G(s)代表着G(s)H(s)

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
1
评论
Dr_Can自动控制理论学习——根轨迹

为常数，可知为另可知根为化简为可知根为和将上式分解可得转换为时域形式当时。
复制链接

扫一扫

CSDN认证博客专家 CSDN认证企业博客

码龄12年

2: 原创

22万+: 周排名

202万+: 总排名

421: 访问

: 等级

23: 积分

0: 粉丝

2: 获赞

2: 评论

0: 收藏

私信

关注

热门文章

最新评论

Dr_Can自动控制理论学习
CSDN-Ada助手: 恭喜Dr_Can开始了自己的博客创作之旅！自动控制理论学习是一个非常深奥的领域，希望你能够分享你的学习心得和体会。接下来，我建议你可以结合实际案例或者应用场景，深入探讨自动控制理论在实际工程中的应用，这样可以让读者更加直观地理解理论知识。期待看到你更多的精彩内容，加油！推荐【每天值得看】：https://bbs.csdn.net/forums/csdnnews?typeId=21804&utm_source=csdn_ai_ada_blog_reply1
Dr_Can自动控制理论学习——根轨迹
CSDN-Ada助手: 评论：非常感谢您持续创作并分享这篇关于Dr_Can自动控制理论学习的博文！您对根轨迹的介绍让我对这个概念有了更深入的了解。继续努力，我期待您未来更多的博客！除了根轨迹，关于自动控制理论还有一些相关的扩展知识和技能可以进一步探索。例如，您可以继续介绍极点、零点和其对系统稳定性的影响，以及如何通过根轨迹设计控制器的方法。此外，您还可以探讨如何使用MATLAB或其他控制工具进行根轨迹分析和设计。谦虚地说，我相信您对这些扩展知识和技能的分享一定会让读者们更加全面地理解和应用自动控制理论。期待您未来更多的精彩博文！如何写出更高质量的博客，请看该博主的分享：https://blog.csdn.net/lmy_520/article/details/128686434?utm_source=csdn_ai_ada_blog_reply2
Dr_Can自动控制理论学习
CSDN-Ada助手: 恭喜你这篇博客进入【CSDN每天最佳新人】榜单，全部的排名请看 https://bbs.csdn.net/topics/617305225。

大家在看

最新文章

Dr_Can自动控制理论学习

目录

评论 1

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。