Dr_Can自动控制理论学习

ysh12345678gok

已于 2023-09-23 23:00:48 修改

阅读量256

点赞数 2

文章标签：学习

于 2023-09-23 12:04:26 首次发布

本文链接：https://blog.csdn.net/ysh12345678gok/article/details/133202390

版权

本文部分素材来自Dr_Can的B站教程，请支持原作者。DR_CAN的个人空间-DR_CAN个人主页-哔哩哔哩视频 (bilibili.com)

1.系统稳定性

三种稳定情况，一共分为不稳定、临界稳定和稳定三种状态，不稳定在输入情况下输出不确定范围跳动，临界稳定输入在限定范围内，输出在规定的范围内波动，图中举例为平衡车，身体前倾看作有界的输入，平衡车跟随输入有界输出，超出范围后系统失去稳定性，稳定系统在时间为无穷大时，最终的结果都会趋于稳定。

2.闭环传递函数

$(V(s)-X(s) H(s))(D(s) G(s))=X(s)$

最后化简

$X(s)=\frac{V(s)D(s) G(s)}{1+H(s)D(s) G(s))}$

再变成传递函数的形式

$\frac{X(s)}{V(s)}=\frac{D(s) G(s)}{1+H(s)D(s) G(s))}$

最终的设计重点变为控制器 $D(s)$ 的稳定性设计和误差分析，实际是把该闭环系统视为“开环系统”，该系统传递函数为 $G(s)_{cl}=\frac{X(s)}{V(s)}=\frac{D(s) G(s)}{1+H(s)D(s) G(s))}$ ,研究 $G(s)_{cl}$ 是否稳定。

此时开环系统与闭环系统输入为单位脉冲 $U(s)$ 与 $R(s)$ ，其拉普拉斯变换后值为1，故追求稳定性的的问题就却决于 $G(s)_{cl}$ 是否收敛。

将得到的传递函数因式分解可以得到如上形式，进行拉普拉斯变换,拉普拉斯变换常用公式如下

$L\left[1\right]=\frac1s \\ L\left[e^{at}\right]=\frac1{s-a} \\ L\left[t^{n}e^{at}\right]=\frac{\Gamma(n+1)}{\left(s-a\right)^{n+1}}\{n>-1\} \\ L\left[t^n\right]=\frac{\Gamma(n+1)}{s^{n+1}}\{n>-1\} \\ L\left[\sin at\right]=\frac a{s^2+a^2} \\ L\left[\cos at\right]=\frac s{s^2+a^2} \\ L\left[\sin\text{h}at\right]=\frac{a}{s^2-a^2} \\ L\left[\cos\text{h}at\right]=\frac s{s^2-a^2} \\ L\left[t\sin at\right]=\frac{2as}{\left(s^2+a^2\right)^2} \\ L\left[t\cos at\right]=\frac{s^2-a^2}{\left(s^2+a^2\right)^2}$

可知例1传递函数可以分解为第二种形式，极点值为-3和2， $e^{-3t}$ 随时间变化逐渐到， $e^{2t}$ 随时间增大逐渐增大， $t\rightarrow \infty ,e^{2t}\rightarrow \infty$ ,可知 $t\rightarrow \infty , e^{2t}+e^{-3t}\rightarrow \infty$

同理，该系统为逐渐稳定的。

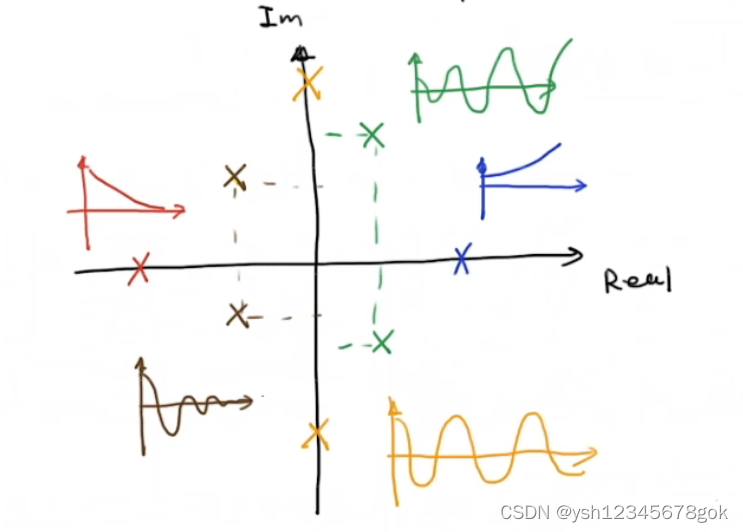
实部的正负影响着系统的稳定性，实部为正系统不稳定随时间增加逐渐发散，实部为负系统逐渐稳定，实部为0，系统震荡不稳定。

3.控制器D(s)研究

（1）比例控制器

下图为肥胖问题的传递函数图，只使用比例控制器控制，R为摄入量，M为体重，D为扰动项。

$[k_{p}(k-m)+D]\frac{1}{7000s+10\alpha}=M$

$m{(t)}=C_{1}e^{0 t}+C_{2}e^{\frac{-10\alpha-k_{p}}{7000}t}$

最终 $m{(t)}$ 稳定与否取决于第二项 $C_{2}e^{\frac{-10\alpha-k_{p}}{7000}t}$ $t\rightarrow \infty$ 时的值，这就用到了下面的结论，要求 $-10\alpha-k_{p}<0$

满足上述条件时 $m{(t)}$ 才有可能实现稳定。

Dr_CAN留问题Kp=-5,含义是什么。

一位同学回答比较好，在此贴出

这个模型里是不是可以把这个Kp看成一个“决心因子”或者“自控因子”，Kp越大，表示你减小差距的愿望越强烈，采取的行动越多。根据系统的根我们知道Kp+10α两个参数共同影响着体重的输出结果。于是当你的决心Kp在代谢率系数10α的承受范围内，即Kp>-13时，体重总是可控的，而且愿望越强烈，就能越快达到目标。
Kp>0说明你比较节制，只要体重超过预期，就会采取行动减肥；
Kp=0说明you just dont care，不会因为体重和预期有差距而产生任何行动，任由干扰项身体代谢率 do the job，
Kp<0（比如-5）说明你就算体重超过预期仍然快乐养膘，这时只要你的快乐程度没有战胜基础代谢率（系统自身的稳定性储备），那么体重虽然慢但仍然早晚可以依靠自然代谢率降下来。但是如果你看到自己越胖约开心，主观上加大力度继续变胖，自控因子Kp<-13，身体代谢率也救不了你的时候，你的体重就会疯狂爆炸。

总结：Kp正负决定着反馈的正负，超出限定值系统失去稳定性，（系统自身的稳定性储备）<输入反馈。