附注-三维空间的线性变化
前情提要
前面说了向量和变换矩阵的关系，但是只说明了一类将二维向量变换为其它二维向量的特殊变换
总的来说这个课程一直在二维空间上考量这个问题，也更容易理解，并且你掌握了二维空间的核心概念这些概念也能推广到高维度空间
三维空间
现在我们那么考量一个函数
[
2
6
−
1
]
i
n
p
u
t
→
L
(
v
⃗
)
→
[
3
2
0
]
o
u
t
p
u
t
\left[ \begin{matrix} 2 \\ 6 \\ -1 \\ \end{matrix} \right]_{input} \rightarrow L(\vec{v}) \rightarrow \left[ \begin{matrix} 3\\ 2\\ 0\\ \end{matrix} \right]_{output}
26−1
input→L(v)→
320
output
我们可以想象一个三维空间内的所有点经历了一个线性变换
保持网格线平行且等距，并保持原点不动
保持网格线平行且等距，并保持原点不动
保持网格线平行且等距，并保持原点不动
和二维类似我们看到的三维空间的每一个点实际上只是代表一个以它为终点的一个向量而我们所做的只是把输入的向量移动到对应的输出向量。
和二维情况类似，三维的线性变换完全由基向量的去向决定
但是我们现在有三个使用的基向量
i
^
,
j
^
,
k
^
\widehat{i},\widehat{j},\widehat{k}
i
,j
,k
变换矩阵
接下来我们仍然留下原始坐标作为副本
这样我们就能观察到三个基向量的变化
将变化后的基向量坐标记录在一个3x3的矩阵中
[
1
1
1
0
1
0
−
1
0
1
]
\left[ \begin{matrix} 1 & 1 & 1\\ 0 & 1 & 0\\ -1 & 0 & 1\\ \end{matrix} \right]
10−1110101
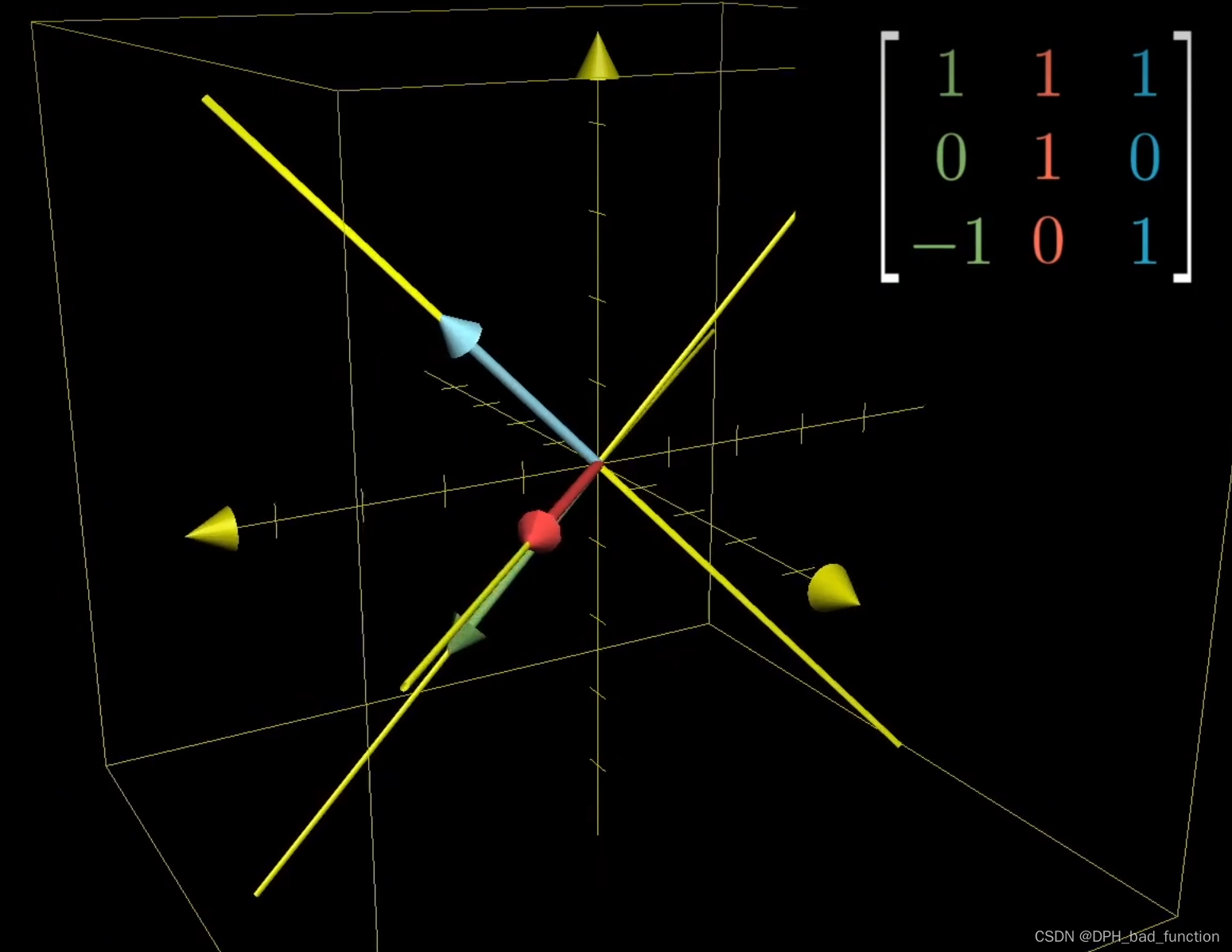
考虑个简单的例子，沿着y轴旋转90°
那么它的变化矩阵就会是
[
0
0
1
0
1
0
−
1
0
0
]
\left[ \begin{matrix} 0 & 0 & 1\\ 0 & 1 & 0\\ -1 & 0 & 0\\ \end{matrix} \right]
00−1010100
想知道任意向量在变换后的去向？
其实是和二维空间一样的
而且二维空间“缩放再相加”的过程再变换前后都可以用
所以想得到一个向量变化后的位置其实还是在做乘法的
[
0
1
2
3
4
5
6
7
8
]
t
r
a
n
s
f
o
r
m
a
t
i
o
n
[
x
y
z
]
i
n
p
u
t
=
(
x
[
0
3
6
]
+
y
[
1
4
7
]
+
z
[
2
5
8
]
)
o
u
t
p
u
t
\left[ \begin{matrix} 0 & 1 & 2\\ 3 & 4 & 5\\ 6 & 7 & 8\\ \end{matrix} \right]_{transformation} \left[ \begin{matrix} x\\ y\\ z\\ \end{matrix} \right]_{input}= (x\left[ \begin{matrix} 0\\ 3\\ 6\\ \end{matrix} \right]+ y\left[ \begin{matrix} 1\\ 4\\ 7\\ \end{matrix} \right]+ z\left[ \begin{matrix} 2\\ 5\\ 8\\ \end{matrix} \right])_{output}
036147258
transformation
xyz
input=(x
036
+y
147
+z
258
)output
考量两个连续的线性变化也是一样的参考二维空间的就可以了
后续
下一节是行列式，记完下个笔记，就去看MIT的线代了。
2538
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
