#行列式及其几何意义
我们来考察之前说的线性变换，我们注意到它们对整个空间进行放缩
有件事对于我们理解线性变换很有帮助，就是测量对于空间的放缩程度
更具体一点就是一个给定区域的变化比例
举个例子
[
3
0
0
2
]
,
在这里
i
^
延长了
3
倍，
j
^
被延长了
2
倍数，显然这个系数是
6
\left[ \begin{matrix} 3 & 0\\ 0 & 2\\ \end{matrix} \right],在这里\widehat{i}延长了3倍，\widehat{j}被延长了2倍数，显然这个系数是6
[3002],在这里i
延长了3倍，j
被延长了2倍数，显然这个系数是6
接下来考虑一个剪切矩阵
[
1
1
0
1
]
,
也就意味着
i
^
保持不变
j
^
移动到
(
1
,
1
)
\left[ \begin{matrix} 1 & 1\\ 0 & 1\\ \end{matrix} \right],也就意味着\widehat{i}保持不变\widehat{j}移动到(1,1)
[1011],也就意味着i
保持不变j
移动到(1,1)
但它的系数仍为一，因为它张开的平行四边形的面积并没有改变。所以哪怕你向右挤压他，他仍有可能不改变这个系数，实际上你只需要知道这个比例就能告诉你任意空间的比例
这个比例其实就是
d
e
t
(
[
3
2
0
2
]
)
=
6
det( \left[ \begin{matrix} 3 & 2\\ 0 & 2\\ \end{matrix} \right] )=6
det([3022])=6
如果一个式子的det是1/2则它张成的面积应该被缩小一半
如果是0，则称这些向量存在线性相关
如果它的det为-1实际上是对空间的一个翻转
那么我们知道
a
b
s
(
d
e
t
(
M
1
)
)
是面积的缩放比例，而正负表示是否对空间进行翻转
abs(det(M1))是面积的缩放比例，而正负表示是否对空间进行翻转
abs(det(M1))是面积的缩放比例，而正负表示是否对空间进行翻转
三维空间
在三维中正方体经过线性变化是一个平行六面体
而负值对于三维空间其实是右手定则的方向的翻转
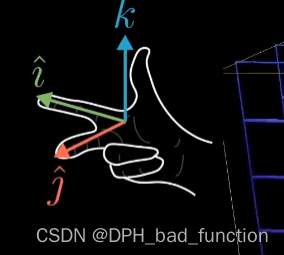
二阶行列式计算通式
d
e
t
(
M
1
)
=
a
d
−
b
c
det(M1)=ad-bc
det(M1)=ad−bc
并且所有的n阶行列式计算都有一个结合律
d
e
t
(
M
1
M
2
)
=
d
e
t
(
M
1
)
d
e
t
(
M
2
)
det(M1M2)=det(M1)det(M2)
det(M1M2)=det(M1)det(M2)
这是显而易见的因为这是一个连续的liner transformation的过程
1363
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
