目录
改进的灰狼优化器(Improved Grey Wolf Optimizer,I-GWO),是由科院二区期刊“Expert Systems with Applications”上文章“An improved grey wolf optimizer for solving engineering problems”提出的。

01.引言
改进的灰狼优化器(Improved Grey Wolf Optimizer,I-GWO),用于解决全局优化和工程设计问题。这种改进是为了解决GWO算法缺乏种群多样性、开发与探索不平衡以及过早收敛等问题。I- GWO算法得益于一种新的运动策略,即基于维度学习的狩猎(DLH)搜索策略,该策略继承自自然界狼的个体狩猎行为。DLH使用不同的方法为每只狼构建一个邻域,在这个邻域中狼之间可以共享邻域信息。DLH搜索策略中使用的维度学习增强了局部搜索和全局搜索之间的平衡,并保持了多样性。在CEC 2018基准测试套件和四个工程问题上对所提出的I-GWO算法的性能进行了评估。在所有实验中,将I-GWO与其他六种最先进的元启发式方法进行比较。结果还通过Friedman和MAE统计检验进行了分析。实验结果和统计测试表明,与实验中使用的算法相比,I-GWO算法具有很强的竞争力,并且往往优于实验中使用的算法。该算法在工程设计问题上的应用证明了它的有效性和适用性。
02.代码流程图


03.部分代码
% Improved Grey Wolf Optimizer (I-GWO)
function [Alpha_score,Alpha_pos,Convergence_curve]=IGWO(N,Max_iter,lb,ub,dim,fobj)
lu = [lb .* ones(1, dim); ub .* ones(1, dim)];
% Initialize alpha, beta, and delta positions
Alpha_pos=zeros(1,dim);
Alpha_score=inf; %change this to -inf for maximization problems
Beta_pos=zeros(1,dim);
Beta_score=inf; %change this to -inf for maximization problems
Delta_pos=zeros(1,dim);
Delta_score=inf; %change this to -inf for maximization problems
% Initialize the positions of wolves
Positions=initialization(N,dim,ub,lb);
Positions = boundConstraint (Positions, Positions, lu);
% Calculate objective function for each wolf
for i=1:size(Positions,1)
Fit(i) = fobj(Positions(i,:));
end
% Personal best fitness and position obtained by each wolf
pBestScore = Fit;
pBest = Positions;
neighbor = zeros(N,N);
Convergence_curve=zeros(1,Max_iter);
iter = 0;% Loop counter
%% Main loop
while iter < Max_iter
for i=1:size(Positions,1)
fitness = Fit(i);
% Update Alpha, Beta, and Delta
if fitness<Alpha_score
Alpha_score=fitness; % Update alpha
Alpha_pos=Positions(i,:);
end
if fitness>Alpha_score && fitness<Beta_score
Beta_score=fitness; % Update beta
Beta_pos=Positions(i,:);
end
if fitness>Alpha_score && fitness>Beta_score && fitness<Delta_score
Delta_score=fitness; % Update delta
Delta_pos=Positions(i,:);
end
end
%% Calculate the candiadate position Xi-GWO
a=2-iter*((2)/Max_iter); % a decreases linearly from 2 to 0
% Update the Position of search agents including omegas
for i=1:size(Positions,1)
for j=1:size(Positions,2)
r1=rand(); % r1 is a random number in [0,1]
r2=rand(); % r2 is a random number in [0,1]
A1=2*a*r1-a; % Equation (3.3)
C1=2*r2; % Equation (3.4)
D_alpha=abs(C1*Alpha_pos(j)-Positions(i,j)); % Equation (3.5)-part 1
X1=Alpha_pos(j)-A1*D_alpha; % Equation (3.6)-part 1
r1=rand();
r2=rand();
A2=2*a*r1-a; % Equation (3.3)
C2=2*r2; % Equation (3.4)
D_beta=abs(C2*Beta_pos(j)-Positions(i,j)); % Equation (3.5)-part 2
X2=Beta_pos(j)-A2*D_beta; % Equation (3.6)-part 2
r1=rand();
r2=rand();
A3=2*a*r1-a; % Equation (3.3)
C3=2*r2; % Equation (3.4)
D_delta=abs(C3*Delta_pos(j)-Positions(i,j)); % Equation (3.5)-part 3
X3=Delta_pos(j)-A3*D_delta; % Equation (3.5)-part 3
X_GWO(i,j)=(X1+X2+X3)/3; % Equation (3.7)
end
X_GWO(i,:) = boundConstraint(X_GWO(i,:), Positions(i,:), lu);
Fit_GWO(i) = fobj(X_GWO(i,:));
end
%% Calculate the candiadate position Xi-DLH
radius = pdist2(Positions, X_GWO, 'euclidean'); % Equation (10)
dist_Position = squareform(pdist(Positions));
r1 = randperm(N,N);
for t=1:N
neighbor(t,:) = (dist_Position(t,:)<=radius(t,t));
[~,Idx] = find(neighbor(t,:)==1); % Equation (11)
random_Idx_neighbor = randi(size(Idx,2),1,dim);
for d=1:dim
X_DLH(t,d) = Positions(t,d) + rand .*(Positions(Idx(random_Idx_neighbor(d)),d)...
- Positions(r1(t),d)); % Equation (12)
end
X_DLH(t,:) = boundConstraint(X_DLH(t,:), Positions(t,:), lu);
Fit_DLH(t) = fobj(X_DLH(t,:));
end
%% Selection
tmp = Fit_GWO < Fit_DLH; % Equation (13)
tmp_rep = repmat(tmp',1,dim);
tmpFit = tmp .* Fit_GWO + (1-tmp) .* Fit_DLH;
tmpPositions = tmp_rep .* X_GWO + (1-tmp_rep) .* X_DLH;
%% Updating
tmp = pBestScore <= tmpFit; % Equation (13)
tmp_rep = repmat(tmp',1,dim);
pBestScore = tmp .* pBestScore + (1-tmp) .* tmpFit;
pBest = tmp_rep .* pBest + (1-tmp_rep) .* tmpPositions;
Fit = pBestScore;
Positions = pBest;
%%
iter = iter+1;
neighbor = zeros(N,N);
Convergence_curve(iter) = Alpha_score;
end
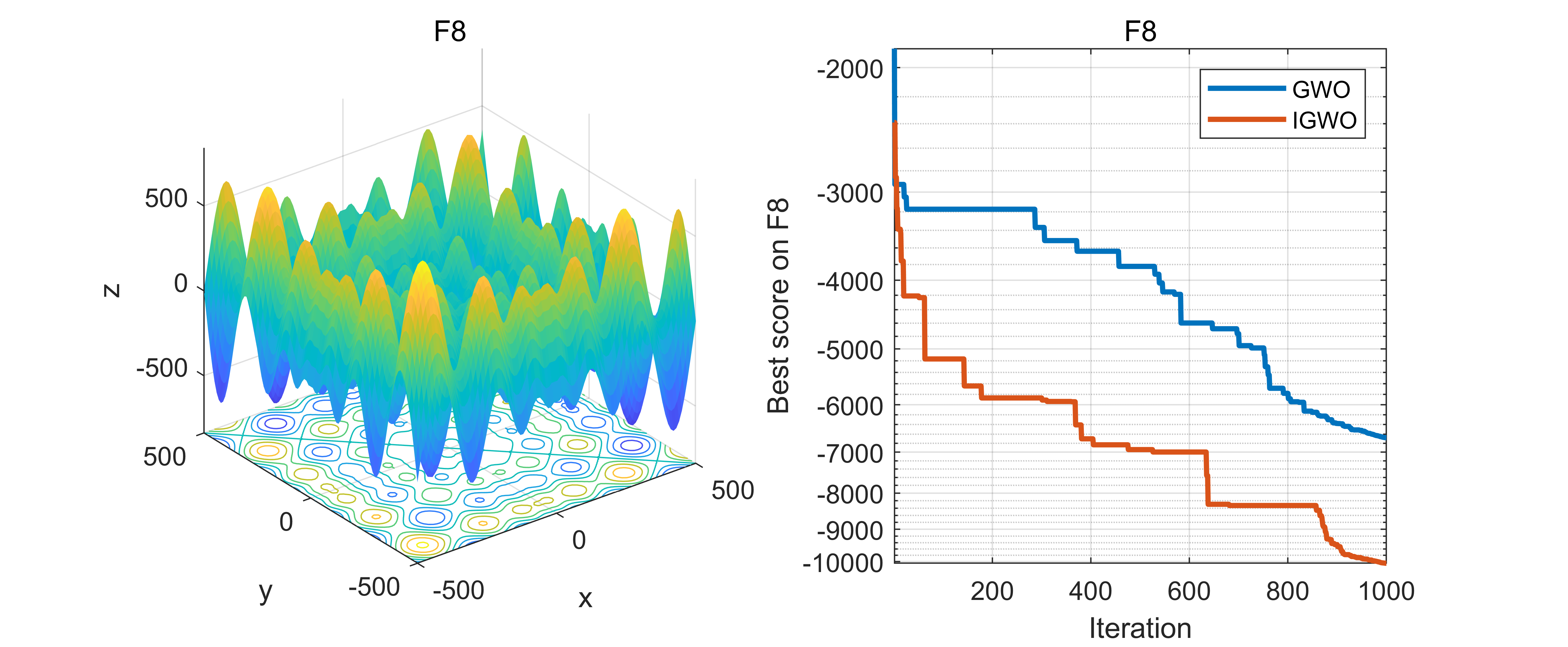
end04.代码效果图





获取代码请关注MATLAB科研小白的个人公众号(即文章下方二维码),并回复:智能优化算法本公众号致力于解决找代码难,写代码怵。各位有什么急需的代码,欢迎后台留言~不定时更新科研技巧类推文,可以一起探讨科研,写作,文献,代码等诸多学术问题,我们一起进步。

























 412
412

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










