数据结构——二叉树的顺序结构及实现（堆）

Massachusetts_11

已于 2022-04-19 22:57:29 修改

阅读量3.2k

点赞数 15

于 2022-04-10 05:46:12 首次发布

本文链接：https://blog.csdn.net/yue152152/article/details/124071559

版权

数据结构专栏收录该内容

10 篇文章 6 订阅

订阅专栏

前言

此文章主要讲解二叉树的顺序结构，堆的实现。在阅读本文之前，希望大家可以对二叉树进行一定程度了解。

数据结构——树与二叉树_Massachusetts_11的博客-CSDN博客

1. 二叉树的顺序结构

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

2.堆的概念及结构

以上是堆的定义，看不懂不重要，我们接下来慢慢解释：

1.首先堆必须时一棵完全二叉树

2.堆一般分为两种：

小根堆：任意一个节点的两个子节点都比自己的值大或相等，也就是根最小，整个二叉树从上到下递增。

大根堆：任意一个节点的两个子节点都比自己的值小或相等，也就是根最大，整个二叉树从上到下递减。

转换原理：

那么问题来了，这里的存储结构是如何向逻辑结构去实现的呢？

不知大家是否还记得树与二叉树一文中二叉树性质的这几条

也就是说：对于任意一个节点，我们设它的下标为i，则它的左孩子节点下标就是2*i +1 ，右孩子就是2*i + 2，父节点下标就是（i - 1) / 2。

（可能大家也发现了，这里的父节点如果用两个子节点去倒推应该有两个不同的结果，但我们所求的下标必须是一个整型，由于c语言向零取整的原则，两个表达式可合成一个（i - 1) / 2 ）

我们不妨来验证一下：

这里元素28的下标是4，它的父节点下标计算后是（4-1）/ 2 = 1，恰好是18元素

它的左子节点2*4+1 = 9，恰好是37元素，它的右子节点2*4+2 = 10，恰好是10元素。

有了以上这些基础，我们也可以进行一下堆的实现了。

3. 堆的实现

与顺序表相同，我们同样也实现一下堆的增删查改

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	size_t size;
	size_t capacity;
}HP;
//初始化堆
void HeapInit(HP* php);
//销毁堆
void HeapDestroy(HP* php);
//打印堆
void HeapPrint(HP* php);
//尾插元素
void HeapPush(HP* php, HPDataType x);
//头删元素
void HeapPop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//计算节点个数
size_t HeapSize(HP* php);
//返回堆头节点
HPDataType HeapTop(HP* php);

3.1初始化

既然要实现，我们就需要从物理存储角度去思考。

与动态顺序表相同，我们为堆设置一个数组，同时为它附加两个记录：元素个数和容量大小（方便扩容）

在没有元素之前，数组置空，元素个数和容量都为0，后续在尾插元素时，再对堆进行判断，进行扩容

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;
}

3.2销毁

对静态开辟的数组进行释放；

元素个数和容量都置零；

void HeapDestroy(HP* php)
{
	assert(php);
	assert(php->a);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

3.2打印

可以选择打印出二叉树的外形，但太复杂了🥶，我们这里仅仅遍历打印了数组，如果各位大神有实现树状打印的可以在讨论区分享一下哈哈哈哈哈

void HeapPrint(HP* php)
{
	assert(php);
	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}

3.3尾插

我们的重头戏终于来了。

这里我们尾插后一定要保证它依旧还是大堆或者小堆，所以我们要先实现一下向上调整的算法，用来保证我们每次插入的元素都能向上插入自己该去的地方。

向上调整算法

以下讲解都以小堆为例，首先上个图免得想不到

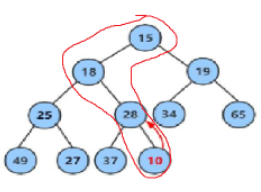
这里，我们想把元素10向上调整，在看这个具体案例之前，我们先了解一下原则：

让当前节点与父节点进行比较，若小于父节点，则交换两节点，接下来判断父节点与父节点的父节点，以此类推，直至出现当前节点不大于父节点。

我们来看一下它的可行性：

每次交换后都能保证父节点为首的这棵子树是堆，如这一次交换就保证了下面这个红圈是个堆

当下一次交换：10位置与18位置交换，说明原来10位置的数比18位置的小，也一定比25位置的小，也就是左右都比10大，这时又保证了大三角是个堆

以此类推，直至大三角框住整棵树，此时整棵树就成堆了。

看一下代码：

这里这个交换可以写个函数，方便表示，以后也能用：

void Swap(HPDataType* pa, HPDataType* pb)
{
	assert(pa && pb);
	HPDataType tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

向上调整：

void AdjustUp(HPDataType* a, size_t child)
{
	assert(a);
	size_t parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}

	}
}

有了向上调整的算法，插入元素就好解决了，但不能忘了我们这是一个动态堆，就要实现可扩容，

于是每次插入之前都要判断是否数组已满或者没容量，而进行扩容，最后才是我们的向上调整算法。

上代码：

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		size_t newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc failed\n");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	php->a[php->size] = x;
	AdjustUp(php->a, php->size);
	php->size++;
}

3.4头删

首先，我们想一下，可以把头元素删掉，后面的元素向前移动吗？

答案肯定是不行的，且不说这个O(N)的算法有点蠢，当我们把所有元素往前挪，这时节点之间的父子关系都被破坏了，十有八九它就不是个堆了，那我们就看看这种方法：

1.第一个数（根位置）和最后一个数进行交换。

2.删除最后一个数（size--就行）

3.把头顶的那个大数字再用一定的方式往下调，调成一个堆。

这时我们就需要一个下调整的算法。

向下调整算法

同样摆个图先看着，这里我们要把28向下调.

向下调整原则：

1.找出左右孩子中小的那个；

2.跟父亲比较，如果父亲小，交换；

3.从交换的孩子位置继续往下调。

可行性分析：

其实向下调整就是为了保证头插的元素通过向下调可以让这个二叉树又形成堆，

调整过程中，挑个小的换，就能保证红圈以外是个堆

再换一次，红圈继续缩：

直到最后没有子节点，也就是圈缩成是一个元素，这时就成堆了

向下调整代码：

void AdjustDown(HPDataType*a,size_t size,size_t root)
{
	assert(a);
	size_t parent = root;
	size_t child = parent * 2 + 1;
	while (child < size)
	{
		if (child+1<size&& a[child + 1] < a[child]  )
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}

	}
}

头删代码;

void HeapPop(HP* php)
{
	assert(php);
	Swap(php->a, &php->a[php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

3.5剩余

剩余函数较简单，相信大家一看就明白了

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}
size_t HeapSize(HP* php)
{
	assert(php);
	return php->size;
}
HPDataType HeapTop(HP* php)
{
	assert(php);
	return php->a[0];
}

4.堆——总代码

4.1 头文件：Heap.h

注：这里默认是小堆，如果对头文件BIGHEAP的宏进行解引用可实现大堆

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
#include<math.h>
//#define BIGHEAP//若大堆，则解除注释,否则加注释
#define SIGN <
#ifdef BIGHEAP
#undef SIGN
#define SIGN >
#endif

// 小堆
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	size_t size;
	size_t capacity;
}HP;

void Swap(HPDataType* pa, HPDataType* pb);
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPrint(HP* php);

// 插入x以后，保持他依旧是(大/小)堆
void HeapPush(HP* php, HPDataType x);

// 删除堆顶的数据。(最小/最大)
void HeapPop(HP* php);
bool HeapEmpty(HP* php);
size_t HeapSize(HP* php);
HPDataType HeapTop(HP* php);

4.2源文件：Heap.c

#include"Heap.h"

void Swap(HPDataType* pa, HPDataType* pb)
{
	assert(pa && pb);
	HPDataType tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}
void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;
}
void HeapDestroy(HP* php)
{
	assert(php);
	assert(php->a);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}
void HeapPrint(HP* php)
{
	assert(php);
	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}
void AdjustUp(HPDataType* a, size_t child)
{
	assert(a);
	size_t parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] SIGN a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}

	}
}
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		size_t newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc failed\n");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	php->a[php->size] = x;
	AdjustUp(php->a, php->size);
	php->size++;
}
void AdjustDown(HPDataType*a,size_t size,size_t root)
{
	assert(a);
	size_t parent = root;
	size_t child = parent * 2 + 1;
	while (child < size)
	{
		if (child+1<size&& a[child + 1] SIGN a[child]  )
		{
			child++;
		}
		if (a[child] SIGN a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}

	}
}
void HeapPop(HP* php)
{
	assert(php);
	Swap(php->a, &php->a[php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}
size_t HeapSize(HP* php)
{
	assert(php);
	return php->size;
}
HPDataType HeapTop(HP* php)
{
	assert(php);
	return php->a[0];
}

4.3测试文件：test.c

#include"Heap.h"
int main()
{
	HP h;
	HeapInit(&h);
	HeapPush(&h, 2);
	HeapPush(&h, 5);
	HeapPush(&h, 7);
	HeapPush(&h, 1);
	HeapPush(&h, 4);
	HeapPrint(&h);
	HeapPop(&h);
	HeapPrint(&h);
	printf("%d", HeapTop(&h));
}

4.4测试结果

5. 堆的应用

5.1堆排序

堆排序即使用堆的思想进行排序，总共分为两个步骤：

1.建堆

2.利用堆删除的思想进行排序

5.1.1基础版本

我们先上个简单的版本，用刚刚实现的堆来完成堆排序。

整体思路为：

1.首先新建一个堆，遍历整个数组，将所有元素Push到堆中。

2.此时如果是小堆，那堆首元素一定最小，我们就将这个元素存入数组，然后把这个元素从堆中头删掉。

3.循环第二个动作，直至将堆清空。

代码：

void HeapSort(int* a,size_t size)
{
	HP hp;
	HeapInit(&hp);
	//建堆
	for (int i = 0; i < size; i++)
	{
		HeapPush(&hp, a[i]);
	}
	//堆删除
	for (int i = 0; i < size; i++)
	{
		a[i] = HeapTop(&hp);
		HeapPop(&hp);
	}
	HeapDestroy(&hp);
}

我们看一它的时间复杂度：

循环遍历是O(N)；

Push操作最坏情况走的是树的高度步，假设每次都是n个节点，则高度就是logN，也就是O(logN）；

整个建堆过程就是O(N*logN)；

堆删除与建堆基本形同，也是O(N*logN)；

整个堆排序的时间复杂度也就是O(N*logN)。

再来看一下空间复杂度：
我们额外建堆，就需要一个与数组大小相等的数组，空间复杂度也就是O(N);

时间复杂度是O(N*logN)，对于一个堆排序来说就是标准，但空间复杂度的O(N)完全没有必要，我们是否可以在原数组上进行排序呢？而且排个序还要写个堆，未免有些小蠢。那么我们来看看下面的升级版。

5.1.2升级版

原则与上面基本相同，还是建堆、删堆，只不过我们现在要脱离建堆删掉等封装好的函数，直接用算法在数组上原地操作。

5.1.2.1建堆：

先让我们一起回忆一下向上调整，和向下调整这两个算法。

向上调整：从堆尾插入一个元素，只要这个元素经历过一次向上调整算法，他就能找到自己该去的位置，从而有形成一个堆。

向下调整：当堆顶节点的左右子树都是堆，但政整棵二叉树不是堆，这时通过对堆顶元素向下调整就可以形成一个堆。

有了这两个前提，我们再看看怎么原地建堆：

方法1.向上调整建堆：

对数组的第二个元素进行向上调整，此时最前面的两个元素就形成了一个堆。
然后对第三个元素进行向上调整，此时前三个元素又形成一个堆，
再进行第3，4，5个元素向上调整，直至调整完尾元素，此时就原地建好了一个堆。

方法2.向下调整建堆：

相对上面有点难想，上个图先：

这里我们从下面开始，但不是最后一个元素（下面没东西也没法往下调），我们从元素8（尾节点的父节点）开始进行向下调，调整之后，这部分就成了堆：

然后再是对7（数组中8的上一个元素）向下调：

以此逻辑直至整棵树成堆：

3.时间复杂度比较：

从直观上看，遍历是O(N)，向上向下都是O(logN),这两种方式建堆方式的时间复杂都是O(N*logN),但真的是这样吗？

向上调整：

假设最坏的情况：满二叉树，设二叉树的高度为h，第二层有两个节点，每个节点调整一次，第三层有四个节点，每个节点调整两次，第h层有 ${\color{Yellow} }2^{h-1}$ 个节点，每个节点调整h-1次，这一层共调整 $(h-1)\times 2^{(h-1)}$ 次，将第2层到第h层的元素相加， $T(h) = 1\times2+2\times4+...+$ $(h-1)\times 2^{(h-1)}$ ,这是一个等差乘等比的数列，通过错位相减，就是 $T(h) = (h-2)\times2^{h}+2$ ,根据之前的二叉树定理可知 $h=log{_{2}(n+1)}$ ，带入得 $T(n) = (n+1)\times log{_{2}}(n+1)-2\times(n+1)+2$ ,它的时间复杂度就是 ${\color{Red}O(NlogN) }$

向下调整：

还是假设最坏情况：满二叉树，若向下调整，就是从倒数第二层开始逐个向下，倒数第二层有 $2^{h-2}$ 个元素，每个元素向下移动1次，倒数第三行有 $2^{h-3}$ 个元素，每个元素移动2次，……第一行有1个，移动h-1次，从1到h-1层累加，一共 $T(h) = 1\times2^{h-2}+2\times2^{h-3}+...+(h-1)\times1$ ,同样用错位相减， $T(h)=2^{h}-h-1$ ,带入 $h=log{_{2}(n+1)}$ ,得 $T(n) =n-log{_{2}(n+1)}$ ,它的时间复杂度就是O(N).

很明显向下调整的方案更优，但其实多一个logN也满不了多少，一千个数据也就差差十倍，不过能快一点是一点吧👻

5.1.2.2排序（堆删除）

有了建堆的经验，删堆排序也就相对容易了。

一个堆，只有一个位置能确定是最大值或者最小值，那就是堆顶。

能找到这个最值，我们再想想从哪头开始放，从前往后放吗？

如果从前往后放，从第二个位置开始，就不再能从堆顶找到那个次大或者次小值了

于是我们就把这个最值放到末尾，

那么问题来了，原本的末尾元素放哪？

堆顶元素刚走，干脆就放在堆顶，

这个时候问题又来了，这样交换之后上面又不是堆了，解决方式也很简单，向下调整算法啊！把换上去的元素再沉下来。

一顿操作猛如虎，终于第一个元素过去了😅，之后我们就把原本的一个堆分两部分前一部分是堆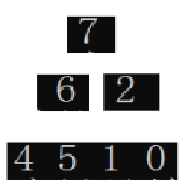，后一部分是存储区（刚刚移过去的元素），前删后增，直至全部排完。

升序排列：想要升序排，就是把大的放后面，也就是说，要先建一个大堆
降序排列：于上相反，建小堆。

总结：

之前我们一直在推理，那么我们现在总结以下，怎么实现堆排序：

建堆：从最后一个有子节点的元开始向前遍历，将每个元素进行向下调整
排序：将头节点循环与<从后往前的每一个元素>交换，同时进行向下调整。

升序堆排序代码呈现：

void HeapSort(int* a, size_t size)
{
    //(size - 1 - 1) / 2 -> 最后一个节点的父节点
	for (int i = (size - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, size, i);
	}
	for (int i = 0; i < size-1; i++)
	{
        //交换首尾元素，此时尾的下标为size - 1 - i
		Swap(&a[0], &a[size - 1 - i]);
        //此时下沉范围为0到被交换的尾的前一个，它的下标是size - 2 - i，长度是size - 1 - i
		AdjustDown(a, size - 1 - i, 0);
	}
}

测试：

int main()
{
	int arr[] = { 4,3,5,9,8,7,6,5,4,3,2,1 };
	HeapSort(arr, sizeof(arr) / sizeof(arr[1]));
	for (int i = 0; i < sizeof(arr) / sizeof(arr[1]); i++)
	{
		printf("%d ", arr[i]);
	}
}

5.2TopK问题

题目：

TOP-K问题：即求一组数据中前K个最大的元素或者最小的元素。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

分析：

如果数据量不大，是栈区（虚拟内存中的栈的概念）能处理的量，那很简单，用堆排序的思想，直接让所有元素进堆，然后输出前k个就可以了。

但是如果数据量很大，甚至数据量超过了内存区的大小，那就不可能把全部元素同时排到堆中去（我们建堆的操作只能在内存中完成），所以就要想其他方式：

首先建一个k个元素大小的堆，把所有元素中前k个存到堆中；

前k个最大的元素，则建小堆
前k个最小的元素，则建大堆

2.遍历剩余所有元素，分别与堆顶元素进行比较，若大于堆顶元素，则用这个元素覆盖堆顶元素，然后进行向下调整（这里我们以寻找最大的前k个为例，找小的改变条件即可）

实现：

这里只进行算法原理演示，就在栈区简单模拟生成一些数字，就不再去外存获取数据了，如果对文件操作感兴趣，可以看一下这篇文章C语言文件：操作

代码呈现：

void PrintTopK(int* a, int n, int k)
{
	int* kHeap = (int*)malloc(sizeof(int) * k);
	assert(kHeap);
	//录入前k个元素
	for (int i = 0; i < k; i++)
	{
		kHeap[i] = a[i];
	}
	//建一个k个元素的小堆
	for (int i = k-1; i >=0; i--)
	{
		AdjustDownS(kHeap, k, i);
	}
	//遍历剩余数据与堆顶进行比较，替换，下沉
	for (int i = k; i < n; i++)
	{
		if (a[i] > kHeap[0])
		{
			kHeap[0] = a[i];
			AdjustDownS(kHeap, k, 0);
		}
	}
    //打印
	for (int i = 0; i <k; i++)
	{
		printf("%d ", kHeap[i]);
	}
}

测试：

void TestTopk()
{
	int n = 10000;
	int* a = (int*)malloc(sizeof(int) * n);
	srand(time(0));
    //随机生成10000个元素
	for (size_t i = 0; i < n; ++i)
	{
		a[i] = rand() % 1000000;
	}
    //手动输入最大的便于验证
	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[115] = 1000000 + 5;
	a[2305] = 1000000 + 6;
	a[99] = 1000000 + 7;
	a[76] = 1000000 + 8;
	a[423] = 1000000 + 9;
	a[0] = 1000000 + 1000;
	PrintTopK(a, n, 10);
}

//topk测试
int main()
{
	TestTopk();
}

结果：