参数寻优：梯度下降/牛顿下降法 追根溯源

参数寻优

参数寻优背景

　　参数寻优问题随处可见，举几个例子。
　　1. 小明假期结束回校，可以坐火车，可以坐汽车，可以坐飞机，还可以走着，小明从哪条路去学校更好呢？
　　2. 简单的数学，一元二次方程求根。
　　3. 高深的数学，七桥问题，怎么才能通过所有的桥各自一次走回七点所在的岸边。
　　4. 机器学习中，求代价函数在约束条件下的最优解问题。
　　其上四个问题，均是参数寻优问题。问题1中，小明可以通过试探法将所有的方式计算一下时间成本，经济成本，舒适程度，来选择一个性价比最合适的返校方式。问题2中，可以通过一元二次方程的求根公式直接求出解来。问题3中，七桥问题则是典型的图论问题，通过抽象为图，推理得出该题无解。问题4中，机器学习则是数值分析中方程的迭代解法。

本文目标

　　本文主要讲清楚梯度下降法、牛顿下降法是如何想到并引入参数寻优中的，以及他们为什么有效。

参数寻优的迭代法的基本原理

　　

　　 图1 一维的二阶代价函数展示 　　

　　 图2 二维的二阶代价函数展示 　　
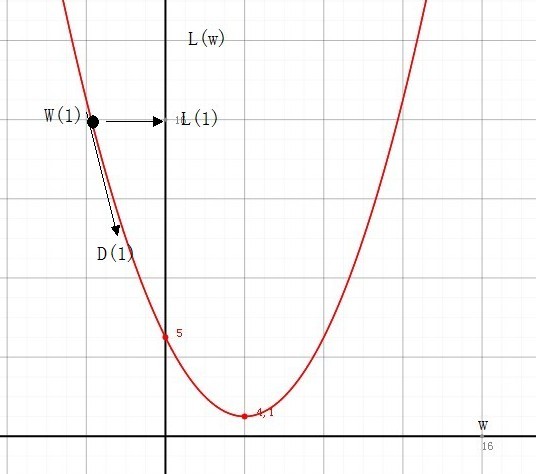
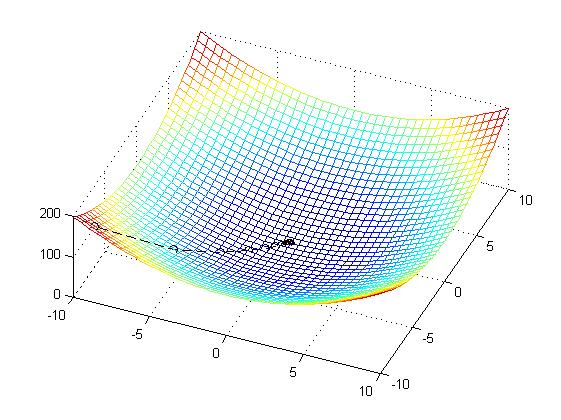
　　通过 代价函数的形状，我们很自然地想到，如果我们从任意一个参数点出发，是否可以找到刚好是让代价下降的方向，沿着这个方向，一定能找到当前的极值点。
　　于是，迭代法参数寻优的基本原理有了： 沿着（代价）函数下降的方向寻找参数，能够找到极值点。

梯度下降法的引入

　　在我们已经学过的数学知识中，导数和方向导数是能找到函数变化方向的。导数表示了曲线的斜率（倾斜度），方向导数表示了曲面沿着任意方向的斜率（倾斜度）。一维时，导数就足够了。但多维时，就需要借助方向导数了，而我们更希望能找到变化率最大的方向。因此，多维下借用方向导数变化最大的情况：梯度，梯度的方向是函数某点增长最快的方向，梯度的大小是该点的最大变化率。
　　三维下，推导方向导数与梯度的关系
　　方向导数：
　　

$\frac{\partial f }{\partial l} = \frac{\partial f}{\partial x}*cos(\alpha)+\frac{\partial f}{\partial y}*cos(\beta)+\frac{\partial f}{\partial z}*cos(\gamma)$
　　 方向： $l = (cos(\alpha), cos(\beta), cos(\gamma))$
　　 梯度： $Grad = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial x}, \frac{\partial f}{\partial x})$