文章目录
一、理论基础
1、人工蜂鸟算法
人工蜂鸟算法(Artificial hummingbird algorithm, AHA)模拟了自然界中蜂鸟的特殊飞行技能和智能觅食策略。建立了三种用于觅食策略的飞行技能模型，包括轴向飞行、对角飞行和全向飞行。此外，还实现了引导觅食、区域性觅食和迁徙觅食，并构建了访问表来模拟蜂鸟对食物来源的记忆功能。
（1）初始化
n
n
n只蜂鸟个体被安置在
n
n
n个食物源上，随机初始化如下：
x
i
=
L
o
w
+
r
⋅
(
U
p
−
L
o
w
)
,
i
=
1
,
2
,
⋯
,
n
(1)
x_i=Low+r\cdot(Up-Low),\quad i=1,2,\cdots,n\tag{1}
xi=Low+r⋅(Up−Low),i=1,2,⋯,n(1)其中，
L
o
w
Low
Low和
U
p
Up
Up分别是
d
d
d维问题的上下边界，
r
r
r是
[
0
,
1
]
[0,1]
[0,1]的随机向量，
x
i
x_i
xi表示第
i
i
i个个体的位置。
食物来源的访问表初始化如下：
V
T
i
,
j
=
{
0
i
≠
j
null
i
=
j
i
=
1
,
⋯
,
n
;
j
=
1
,
⋯
,
n
(2)
VT_{i,j}=\begin{dcases}0\quad\quad\, i≠j\\\text{null}\quad i=j\end{dcases}\,\,i=1,\cdots,n;j=1,\cdots,n\tag{2}
VTi,j={0i=jnulli=ji=1,⋯,n;j=1,⋯,n(2)其中，
i
=
j
,
V
T
i
,
j
=
null
i=j,VT_{i,j}=\text{null}
i=j,VTi,j=null表示蜂鸟在特定的食物来源进食；
i
≠
j
,
V
T
i
,
j
=
0
i≠j,VT_{i,j}=0
i=j,VTi,j=0表示第
i
i
i只蜂鸟在当前迭代中刚刚访问了第
j
j
j个食物源。
（2）引导觅食
每只蜂鸟都有一种自然的倾向，即以最大的花蜜量访问食物源，这意味着目标源需要有较高的花蜜补充率和蜂鸟较长的未访问时间。因此，在AHA中，蜂鸟应该为引导觅食行为确定访问级别最高的食物来源，然后从中选择花蜜补充率最高的食物来源作为其目标食物来源。确定目标食物来源后，蜂鸟可以飞向目标觅食。在觅食过程中，通过引入方向切换向量，AHA算法充分利用并建模了三种飞行技能，包括全向、对角和轴向飞行。该向量用于控制
D
D
D维空间中的一个或多个方向是否为可用。
这些飞行模式可以扩展到
d
−
D
d-D
d−D空间，其中轴向飞行定义如下：
D
(
i
)
=
{
1
i
=
r
a
n
d
i
(
[
1
,
d
]
)
0
e
l
s
e
i
=
1
,
⋯
,
d
(3)
D^{(i)}=\begin{dcases}1\quad i=randi([1,d])\\0\quad else\end{dcases}\quad i=1,\cdots,d\tag{3}
D(i)={1i=randi([1,d])0elsei=1,⋯,d(3)对角飞行的数学模型如下：
D
(
i
)
=
{
1
i
=
P
(
j
)
,
j
∈
[
1
,
k
]
,
P
=
r
a
n
d
p
e
r
m
(
k
)
,
k
∈
[
2
,
⌈
r
1
⋅
(
d
−
2
)
⌉
+
1
]
0
e
l
s
e
i
=
1
,
⋯
,
d
(4)
D^{(i)}=\begin{dcases}1\quad i=P(j),j\in[1,k],P=randperm(k),k\in[2,\lceil{r_1\cdot(d-2)}\rceil+1]\\0\quad else\end{dcases}\quad i=1,\cdots,d\tag{4}
D(i)={1i=P(j),j∈[1,k],P=randperm(k),k∈[2,⌈r1⋅(d−2)⌉+1]0elsei=1,⋯,d(4)全向飞行的定义如下：
D
(
i
)
=
1
i
=
1
,
⋯
,
d
(5)
D^{(i)}=1\quad i=1,\cdots,d\tag{5}
D(i)=1i=1,⋯,d(5)其中，
r
a
n
d
i
(
[
1
,
d
]
)
randi([1,d])
randi([1,d])表示生成一个从1到
d
d
d的随机整数；
r
a
n
d
p
e
r
m
(
k
)
randperm(k)
randperm(k)表示创建一个从1到
k
k
k整数的随机排列；
r
1
r_1
r1是
(
0
,
1
]
(0,1]
(0,1]的随机数。
有了这些飞行能力，蜂鸟就可以访问其目标食物来源，从而获得候选食物来源。因此，根据从所有现有来源中选择的目标食物来源，从旧来源更新食物来源。模拟引导觅食行为和候选食物源的数学方程推导如下：
v
i
(
t
+
1
)
=
x
i
,
t
a
r
(
t
)
+
a
⋅
D
⋅
(
x
i
(
t
)
−
x
i
,
t
a
r
(
t
)
)
(6)
v_i(t+1)=x_{i,tar}(t)+a\cdot D\cdot(x_i(t)-x_{i,tar}(t))\tag{6}
vi(t+1)=xi,tar(t)+a⋅D⋅(xi(t)−xi,tar(t))(6)
a
∼
N
(
0
,
1
)
(7)
a\sim N(0,1)\tag{7}
a∼N(0,1)(7)其中，
x
i
(
t
)
x_i(t)
xi(t)是在第
t
t
t次迭代时第
i
i
i个食物源的位置；
x
i
,
t
a
r
(
t
)
x_{i,tar}(t)
xi,tar(t)是第
i
i
i只蜂鸟计划访问的目标食物源的位置；
a
a
a是一个服从标准正态分布的引导因子。式(6)允许每个当前食物源更新其在目标食物源附近的位置，并通过不同的飞行模式模拟蜂鸟的引导觅食。第
i
i
i个食物源的位置更新如下：
x
i
(
t
+
1
)
=
{
x
i
(
t
)
f
(
x
i
(
t
)
)
≤
f
(
v
i
(
t
+
1
)
)
v
i
(
t
+
1
)
f
(
x
i
(
t
)
)
>
f
(
v
i
(
t
+
1
)
)
(8)
x_i(t+1)=\begin{dcases}x_i(t)\quad\quad\,\,\,\, f(x_i(t))≤f(v_i(t+1))\\v_i(t+1)\quad f(x_i(t))>f(v_i(t+1))\end{dcases}\tag{8}
xi(t+1)={xi(t)f(xi(t))≤f(vi(t+1))vi(t+1)f(xi(t))>f(vi(t+1))(8)其中，
f
(
⋅
)
f(\cdot)
f(⋅)表示函数适应度值。式(8)表明，如果候选食物源的花蜜补充率优于当前食物源的花蜜补充率，蜂鸟将放弃当前食物源，并停留在式(6)中得出的候选食物源处觅食。
在AHA算法中，访问表是存储食物源访问信息的重要组成部分。根据每次迭代的访问表，任何蜂鸟都可以找到它想要访问的目标食物源。访问表记录了自上次同一只蜂鸟访问每个食物来源以来，没有访问它的时间，长时间未访问表示访问级别高。每只蜂鸟都希望选择访问级别最高的食物来源。如果同一最高访问级别有多个源匹配，则蜂鸟将访问的目标食物源选择具有最佳花蜜补充率的源。种群中的每只蜂鸟都通过式(6)访问自己的目标食物源。在每次迭代期间，当蜂鸟使用式(6)对其目标食物源执行引导觅食时，该蜂鸟的其他食物源的访问级别增加1，并且其访问的目标食物源的访问级别初始化为0。在执行引导觅食后，如果没有更好的花蜜补充率，蜂鸟将不会改变其食物来源；如果有更好的花蜜补充率，则当前来源将被新来源取代，然后蜂鸟将留在新的食物来源。相应蜂鸟所在食物源的更新表示所有其他蜂鸟的食物源的访问级别更新。要更新的访问级别设置为其他食物来源的最高级别，增量为1。AHA的引导觅食策略如下图所示。
（3）区域性觅食
蜂鸟在访问了食用花蜜的目标食物来源后，很可能会寻找新的食物来源，而不是访问其他现有的食物来源。因此，蜂鸟可以很容易地移动到自己区域内的邻近地区，在那里可以找到一种新的食物来源，作为可能比目前更好的备选解决方案。模拟蜂鸟在区域性觅食策略和候选食物源中的局部搜索的数学方程如下：
v
i
(
t
+
1
)
=
x
i
(
t
)
+
b
⋅
D
⋅
x
i
(
t
)
(9)
v_i(t+1)=x_i(t)+b\cdot D\cdot x_i(t)\tag{9}
vi(t+1)=xi(t)+b⋅D⋅xi(t)(9)
b
∼
N
(
0
,
1
)
(10)
b\sim N(0,1)\tag{10}
b∼N(0,1)(10)其中，
b
b
b是服从标准正态分布的区域性觅食因子。式(9)可以让任何蜂鸟根据其特殊的飞行技能，根据其个体位置，在其附近轻松找到新的食物来源。执行区域性觅食策略后，应更新访问表。AHA的区域觅食策略如下图所示。
（4）迁徙觅食
当蜂鸟经常造访的地区往往缺乏食物时，这种蜂鸟通常会迁移到较远的食物来源觅食。在AHA算法中，定义了迁徙系数。如果迭代次数超过迁徙系数的预定值，则位于花蜜填充率最差的食物源的蜂鸟将迁徙到在整个搜索空间中随机产生的新食物源。此时，这只蜂鸟将抛弃旧的来源，留在新的来源处觅食，然后更新访问表。蜂鸟从补充花蜜率最差的来源迁移到随机产生的新来源的觅食情况如下：
x
w
o
r
(
t
+
1
)
=
L
o
w
+
r
⋅
(
U
p
−
L
o
w
)
(11)
x_{wor}(t+1)=Low+r\cdot(Up-Low)\tag{11}
xwor(t+1)=Low+r⋅(Up−Low)(11)其中，
x
w
o
r
x_{wor}
xwor是种群中花蜜补充率最差的食物来源。AHA的迁移觅食策略如下图所示。
在AHA中，除了两个常见参数(种群规模和最大迭代次数)外，在考虑是否执行迁移时，只需确定一个控制参数。在最坏的情况下，如果在执行引导觅食和区域性觅食时没有替代所有食物源，蜂鸟将根据每次迭代的访问表依次访问每个食物源作为其目标源。假设有50%的概率在引导觅食或区域觅食之间进行选择，并且在引导觅食中访问其他来源的概率相同。因此，在最坏的情况下，蜂鸟在重复2次后可能会访问与其目标源相同的食物源。在这种情况下，需要执行迁徙觅食策略以改善停滞状态并探索搜索空间。因此，建议将迁徙系数相对于种群规模的定义如下：
M
=
2
n
(12)
M=2n\tag{12}
M=2n(12)
2、AHA伪代码
AHA首先初始化一组随机解和一个访问表。在每次迭代中，执行引导觅食或区域性觅食的概率为50%。引导觅食使蜂鸟能够向它们各自的目标食物源移动，这些食物源由访问表和花蜜补充率决定；区域性觅食迫使蜂鸟扰乱他们自己的领地；每2次迭代执行一次迁徙觅食。这三种觅食行为都使用了三种飞行技能，包括全向、对角和轴向飞行。所有操作和计算都以交互方式执行，直到达到停止标准。最终，具有最佳花蜜补充率的食物源作为全局最优值的近似值返回。下图给出了AHA的伪码。
二、仿真实验与分析
1、函数测试与数值分析
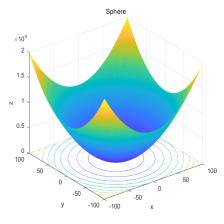
将AHA与SSA、WOA、CS、TLBO和BOA进行对比，以文献[2]中的F1、F2(单峰函数/30维)、F10、F11(多峰函数/30维)、F17、F18(固定维度多峰函数/2维、2维)为例，种群规模设置为50，最大迭代次数设置为1000，每个算法独立运算30次。结果显示如下：
函数：F1
SSA：最差值: 1.1859e-08,最优值:4.861e-09,平均值:8.4526e-09,标准差:1.7138e-09,秩和检验:3.018e-11
WOA：最差值: 2.7816e-171,最优值:5.1364e-189,平均值:1.695e-172,标准差:0,秩和检验:3.018e-11
CS：最差值: 0.016572,最优值:0.00308,平均值:0.0091215,标准差:0.0031982,秩和检验:3.018e-11
TLBO：最差值: 1.0606e-178,最优值:5.0987e-181,平均值:1.409e-179,标准差:0,秩和检验:3.018e-11
BOA：最差值: 1.9231e-14,最优值:1.5141e-14,平均值:1.6978e-14,标准差:9.0632e-16,秩和检验:3.018e-11
AHA：最差值: 3.059e-291,最优值:0,平均值:1.0197e-292,标准差:0,秩和检验:1
函数：F2
SSA：最差值: 3.4463,最优值:0.00096052,平均值:0.94667,标准差:1.0658,秩和检验:3.0199e-11
WOA：最差值: 2.2919e-106,最优值:1.0256e-119,平均值:9.1686e-108,标准差:4.1908e-107,秩和检验:3.0199e-11
CS：最差值: 4.2442,最优值:0.41206,平均值:1.4246,标准差:0.74716,秩和检验:3.0199e-11
TLBO：最差值: 8.822e-89,最优值:1.1342e-90,平均值:9.3691e-90,标准差:1.5917e-89,秩和检验:3.0199e-11
BOA：最差值: 1.1506e-11,最优值:2.7655e-12,平均值:9.5493e-12,标准差:2.3595e-12,秩和检验:3.0199e-11
AHA：最差值: 6.0566e-150,最优值:1.4165e-168,平均值:2.5743e-151,标准差:1.1309e-150,秩和检验:1
函数：F10
SSA：最差值: 4.2114,最优值:1.8958e-05,平均值:1.7828,标准差:0.92461,秩和检验:1.2118e-12
WOA：最差值: 7.9936e-15,最优值:8.8818e-16,平均值:3.7303e-15,标准差:2.3603e-15,秩和检验:8.725e-08
CS：最差值: 13.3722,最优值:2.449,平均值:5.0032,标准差:2.616,秩和检验:1.2118e-12
TLBO：最差值: 4.4409e-15,最优值:4.4409e-15,平均值:4.4409e-15,标准差:0,秩和检验:1.6853e-14
BOA：最差值: 1.2712e-11,最优值:6.2395e-12,平均值:1.0069e-11,标准差:2.1015e-12,秩和检验:1.2118e-12
AHA：最差值: 8.8818e-16,最优值:8.8818e-16,平均值:8.8818e-16,标准差:0,秩和检验:NaN
函数：F11
SSA：最差值: 0.061409,最优值:3.4712e-08,平均值:0.012305,标准差:0.013161,秩和检验:1.2118e-12
WOA：最差值: 0.051552,最优值:0,平均值:0.0031456,标准差:0.012026,秩和检验:0.1608
CS：最差值: 0.14086,最优值:0.039652,平均值:0.078588,标准差:0.02729,秩和检验:1.2118e-12
TLBO：最差值: 4.095e-08,最优值:0,平均值:1.365e-09,标准差:7.4765e-09,秩和检验:0.33371
BOA：最差值: 1.1102e-14,最优值:0,平均值:2.0724e-15,标准差:2.5343e-15,秩和检验:5.7091e-11
AHA：最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
函数：F17
SSA：最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:3.1981e-15,秩和检验:6.349e-05
WOA：最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:4.2233e-07,秩和检验:1.2118e-12
CS：最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:0,秩和检验:NaN
TLBO：最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:0,秩和检验:NaN
BOA：最差值: 0.58607,最优值:0.39789,平均值:0.41226,标准差:0.03864,秩和检验:1.2118e-12
AHA：最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:0,秩和检验:NaN
函数：F18
SSA：最差值: 3,最优值:3,平均值:3,标准差:6.5529e-14,秩和检验:5.2114e-12
WOA：最差值: 3,最优值:3,平均值:3,标准差:4.4543e-06,秩和检验:5.2152e-12
CS：最差值: 3,最优值:3,平均值:3,标准差:1.784e-15,秩和检验:0.025149
TLBO：最差值: 3,最优值:3,平均值:3,标准差:2.0451e-15,秩和检验:0.62618
BOA：最差值: 3.7505,最优值:3.0001,平均值:3.0456,标准差:0.14064,秩和检验:5.2152e-12
AHA：最差值: 3,最优值:3,平均值:3,标准差:1.2749e-15,秩和检验:1
结果表明，AHA在计算量和求解精度方面优于文献中已有的优化算法。
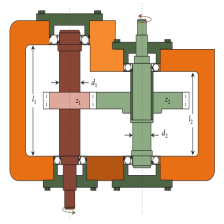
2、求解压缩弹簧设计优化问题
压缩弹簧设计问题具体请参考这里。仿真实验中，6种算法的运行次数、种群规模和最大迭代次数都保持一致，即
N
=
50
,
M
a
x
_
i
t
e
r
=
1000
N=50,Max\_iter=1000
N=50,Max_iter=1000，每种算法分别独立运行30次。结果显示如下：
SSA：最差值: 0.013086,最优值:0.012669,平均值:0.012805,标准差:0.00010274,秩和检验:2.9729e-11
WOA：最差值: 0.017768,最优值:0.012721,平均值:0.013813,标准差:0.001306,秩和检验:2.9729e-11
CS：最差值: 0.012664,最优值:0.012663,平均值:0.012663,标准差:2.386e-08,秩和检验:2.9729e-11
TLBO：最差值: 0.012684,最优值:0.012663,平均值:0.012666,标准差:5.0366e-06,秩和检验:2.9729e-11
BOA：最差值: 22.5896,最优值:0.013201,平均值:0.99649,标准差:4.168,秩和检验:2.9729e-11
AHA：最差值: 0.012663,最优值:0.012663,平均值:0.012663,标准差:1.1939e-13,秩和检验:1
实验结果表明：AHA在求解压缩弹簧设计约束优化问题时具有优越的性能。
3、WSN覆盖优化
本文采用0/1覆盖模型。设监测区域为
50
m
×
50
m
50 m×50 m
50m×50m的二维平面，传感器节点个数
N
=
35
N=35
N=35，其感知半径是
R
s
=
5
m
R_s=5m
Rs=5m，通信半径
R
c
=
10
m
R_c=10m
Rc=10m，迭代500次。初始部署、AHA优化覆盖、AHA算法覆盖率进化曲线如下图所示。
初始部署和最终部署的节点位置及对应的覆盖率分别为：
初始位置：
35.0591 5.2347
25.6518 32.6113
2.4132 13.3024
25.6055 32.9303
7.5279 39.2267
4.4646 17.2521
17.5283 23.0968
6.2728 29.7016
40.4121 12.3942
27.0403 5.8922
48.8571 42.9803
31.4652 49.9767
37.6822 31.7451
7.5834 46.488
15.1663 34.6881
40.964 43.2909
27.4744 41.2386
40.2968 42.3998
10.9409 19.2006
11.3019 16.8711
0.58894 29.7114
1.5991 9.9457
21.2618 4.6656
15.8854 37.0771
24.3206 0.98289
20.8811 42.7015
12.415 2.4427
18.1693 48.2187
18.0554 45.5749
28.3715 21.1697
46.4974 31.6417
39.2601 4.0393
26.8087 29.3194
38.247 2.0572
33.5147 42.6074
初始覆盖率：0.67128
最优位置：
28.9042 39.3569
47.1491 46.2727
38.5881 40.8398
6.5576 10.3037
28.3095 16.5742
12.6975 2.471
4.0251 26.5092
46.0228 16.4301
34.3108 47.62
38.2979 21.5132
14.4087 11.652
38.7418 3.7907
15.7042 48.4327
4.3654 45.3313
4.1036 17.1473
19.4627 19.1472
46.4287 6.7203
36.7182 12.565
20.6318 4.3091
3.2015 36.8294
45.4931 28.1435
13.3882 40.6197
22.5339 11.1561
20.0856 27.6854
28.4925 22.6464
21.3036 36.3488
37.2945 33.2951
3.6598 4.1102
28.5413 31.0967
30.0822 4.4805
34.3246 27.5475
24.5823 46.6666
11.9409 32.6501
47.4622 36.7473
12.1036 22.4816
最优覆盖率：0.92234
实验结果表明，AHA能够有效提升WSN的覆盖率，使得节点分布更加均匀。
三、参考文献
[1] Weiguo Zhao, Liying Wang, Seyedali Mirjalili. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 388: 114194.
[2] Weiguo Zhao, Liying Wang. An effective bacterial foraging optimizer for global optimization[J]. Information Sciences, 2016, 329: 719-735.
扫一扫
511
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
