TileID编码与TileID解码莫顿码NDS与WGS84坐标转换（Python、C++双实现）

本文出现的知识点

• NDS 坐标
• WGS84坐标
• NDS坐标与WGS84坐标转换
• 莫顿码（morton code）
• 墨卡托投影
• Tile Scheme

以上知识点点击链接 Partitioning of Geographic
Data（NDS，导航数据标准中的地理数据分区）
本文章是对以上的一些细节补充，以及代码实现。

莫顿码（Morton Code）

最容易疑惑的就是莫顿码。

莫顿码是将多维数据转化为一维数据的编码。
莫顿编码定义了一条 Z 形的空间填充曲线，因此莫顿编码通常也称Z阶曲线(Z-order curve)。

Morton Code 二维数据（x,y）的编码方式：

在 N 维空间中对于彼此接近的坐标具有彼此接近的莫顿码, 可以应用于为一个整数对产生一个唯一索引。例如，对于坐标系中的坐标点使用莫顿编码生成的莫顿码，可以唯一索引对应的点。
这些索引为“Z”形排序 。
如下图以Z形(左下->右下->左上->右上)分别代表 2×2、4×4、… n² 平方单位：

Z型排列，以及编码过程：

Tile切割规则、Tile Level编码规则

下面图文是演示了tile 切割过程，但是x,y的标记是错误的，先不需要在意。

Tile id 32位各个Level的存储规则

一个Tile ID由32位bit组成。

根据上图的对照变，可以看出 红色的位存储Tile等级，蓝色位不存储，灰色位存储 NDS 横、纵坐标的莫顿码。

WGS84 坐标转化为Tile的过程

我们演示将NDS坐标准换成莫顿码的过程。

比如我们有一个WGS84坐标 （x: 121.00902, y: 30.88306）
根据公式讲WGS84 坐标转化为NDS坐标

nds = wgs84 * 2³²/ 360
2³² = 1 << 32 = 4294967296

nds_x = int(121.00902 * 4294967296 / 360) 
nds_y = int( 30.88306 * 4294967296 / 360)

nds_x = 1443693842 = 01010110000011010000010100010010 (二进制)
nds_y = 368449257  = 00010101111101100001011011101001

此时NDS坐标为32位坐标，
在转化为Tile ID时需对NDS坐标做位舍弃。

比如我们需要 6级Tile ID:

前 16 - level 位 存储tile等级
中间 15 - level 位存储 0 ，占位
后 2 * level + 1 位 DNS坐标的Morton Code

根据 6级 Tile ID编码规则 ： 10位（tile等级 ） + 9位（中间占位）+13位（nds坐标的Morton Code）

实际上 在13位Morton位中，X坐标占用7位，Y坐标占用6位。

那么nds位为什么不是14位，x，y坐标各占用七位？实现偶数位？

**解释一下为啥 Tile ID中的 Morton Code不是 x y 不是对称存储

** 因为在0级tile编码中，只有x轴分割出两段0,1，y 都是0，编码ID为后 00,01，舍去y占位，一级Tile就只有0,1两个ID。而后续无论1级还是13级Tile ，都是在该基础上切割，所以y都舍弃最前编码的0。

x,y分别使用32位存储，
x轴 -2³¹ 到 +2³¹ 对应 -180°到 +180°
y轴 -2³⁰ 到 +2³⁰ 对应-90°到+90°

在32位数中第32位是符号位，所以很好理解NDS的X轴32位坐标对应关系，-2147483648对应-180°
那在NDS 的y周也有表示正负的情况，-1073,741824（-2³⁰） 到 1,073,741,824，

把-1073,741824换算成二进制就比较好理解:
11000000000000000000000000000000

其实y轴在编码的时候把32位舍弃，但是在转换过程中，NDS把y轴的32位设置于31位相同，来表示符号位。
这也可以解释为什么可以舍弃y轴的32位不参与运算，因为y轴的32位永远与31位相同！

这里也可以解释为什么上面的图片标记的x,y是错误的，
这里标记的x,y坐标是莫顿code参与运算的 NDS x,y坐标舍弃不需要参与运算的位后 转成int的标记。

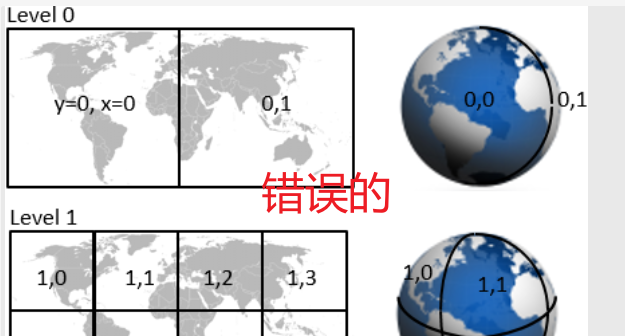
因为对Level 0 进行编码的时候，去x对应wgs 84坐标是 -180 到 +180，对应的x坐标也一定是一负一正，-180°到0°（也就是左侧的Tile）对应NDS的坐标永远是负数，
32表示的第32位永远是1（因为是符号位，都是负数，所以是1），
而在对Level 0 编码的时候 ，只存储1位NDS x坐标，也就是第32位，所以，左侧的x坐标就对应是1。

以下是对NDS坐标Morton编码过程：
使用nds坐标从头到尾编码顺序；

nds_x 选取7位
nds_x = 1443693842 = 0101011 0000011010000010100010010
nds_y 选取7位,舍弃头部一位(因为它永远与31位相同)
nds_y = 368449257 = 0 001010 1111101100001011011101001

6级Tile编码：10位（tile等级 ） + 9位（中间占位）+13位（nds坐标的Morton Code）

坐标信息

	X坐标	Y 坐标
WGS84	121.00902	30.88306
NDS坐标	1443693842	368449257
6级NDS坐标	43	10
6级Tile ID	4195533

NDS坐标与WGS84坐标转换

C++ 实现

#include <cstdint>

int64_t Wgs84ToNds(double x, int tile_level, bool y_flag = false) {
    /**
     * WGS84坐标转NDS坐标计算
     * @param x 坐标
     * @param tile_level tile级别
     * @param y_flag 标记是否是y坐标
     * @return 转换后的NDS坐标
     * 
     * Author DAKANG
     */
    
    if (x == 180.0) {
        x = 179.99999999;
    }
    int64_t v = static_cast<int64_t>(x * 4294967296.0 / 360.0);
    if (v < 0) {
        v = v & 0xFFFFFFFF;
    }
    if (y_flag) {
        v = v & 0x7FFFFFFF;
    }
    return v >> (31 - tile_level);
}

double NdsToWgs84(uint32_t x, int tile_level, bool y_flag = false) {
    uint32_t v = x << (31 - tile_level);
    if (y_flag) {
        v |= (1 << (30 - tile_level));
        v -= (1 << (30 - tile_level));
        if (v & (1 << 30)) {
            v |= 0x80000000;
        }
    }
    int32_t signed_v = static_cast<int32_t>(v);
    return y_flag ? signed_v * 180.0 / (1 << 31)  : signed_v * 360.0 / (1LL << 32);
}

Python 实现

# wgs 84 转 nds
def wgs84_to_nds(x, tile_level, y_flag=False) -> int | Any:
    """
    WGS84坐标转NDS坐标计算
    Parameters
    ----------
    x 坐标
    tile_level tile级别
    y_flag 标记是否是y坐标
	
	Author DAKANG
    Returns
    -------

    """
    if x == 180:
        x = 179.99999999
    v = int(x * 4294967296 / 360)
    if v < 0:
        v = v & 0xFFFFFFFF
    if y_flag:
        v = v & 0x7FFFFFFF
    return v >> (31 - tile_level)
 
# NDS转WGS84
def to_signed_32bit(n):
    n = n & 0xFFFFFFFF
    return n if n < 0x80000000 else n - 0x100000000
def nds_to_wgs84(x, tile_level, y_flag=False):
    """
    NDS坐标转WGS84坐标计算
    Parameters
    ----------
    x 坐标
    tile_level tile级别
    y_flag 标记是否是y坐标
	
	Author DAKANG
	Returns
    -------

    """
    v = x << (31 - tile_level)
    if not y_flag:
        v = to_signed_32bit(v)
        d = v * 360 / (2 ** 32)
    else:
        v |= (2 ** (31 - tile_level - 1))
        v -= (2 ** (31 - tile_level - 1))
        if v & 2 ** 30:
            v |= 0x80000000
        v = to_signed_32bit(v)
        d = v * 180 / (2 ** 31)
    return d

Tile ID转NDS计算

C++ 实现

/**
 * 解析 TileId 为NDS坐标系的横轴坐标
 * @param tile_id 输入tileid
 * @param x 横坐标
 * @param y 纵坐标
 * @date  2024/10/17 18:58
 */
void ParseTileId(const int32_t tile_id, int32_t& x, int32_t& y)
{
    x = 0;
    y = 0;
    int32_t morton_code = tile_id;
    auto current_level = ParseTileLevel(tile_id);
    for (int32_t i = 0; i < current_level + 1; i++)
    {
        auto move_bit = (i * 2);
        x |= (morton_code & 1 << move_bit) >> i;
        y |= (morton_code & 1 << (move_bit + 1)) >> (i + 1);
    }
}

Python 实现

def parse_tile_id_2_nds(tile_id, tile_level=None):
    """
    解析TileID到NDS坐标
    Parameters
    ----------
    tile_id
    tile_level

    Author DAKANG
    Returns
    -------

    """
    nds_x = 0
    nds_y = 0
    morton_code = tile_id
    current_level = parse_tile_level(tile_id)
    for i in range(current_level + 1):
        move_bit = (i * 2)
        nds_x |= (morton_code & 1 << move_bit) >> i
        nds_y |= (morton_code & 1 << (move_bit + 1)) >> (i + 1)
    if current_level == 0 and tile_id == 65537:
        nds_x = 1
    if tile_level:
        nds_x = nds_x >> (current_level - tile_level)
        nds_y = nds_y >> (current_level - tile_level)
    return nds_x, nds_y

NDS、WGS84坐标转Tile ID计算

C++ 实现

int32_t EncodeTileId(const double x, const double y, const int32_t level, const bool is_wgs84)
{
    auto nds_x = 0;
    auto nds_y = 0;

    if (is_wgs84)
    {
        auto _nds_x = std::floor(x * 4294967296 / 360);
        auto _nds_y = std::floor(y * 4294967296 / 360);
        nds_x = static_cast<int32_t>(_nds_x);
        nds_y = static_cast<int32_t>(_nds_y);
        nds_x = nds_x >> (31 - level);
        nds_y = nds_y >> (31 - level);
    }
    else
    {
        nds_x = static_cast<int32_t>(x);
        nds_y = static_cast<int32_t>(y);
    }

    int32_t tile_id = (1 << (level + 16));
    for (int32_t i = 0; i < level + 1; i++)
    {
        tile_id |= (((nds_x & (1 << i)) >> i) << (2 * i));
        tile_id |= (((nds_y & (1 << i)) >> i) << (2 * i + 1));
    }
    return tile_id;
}

Python 实现

def encode_tile_id(x, y, level=13, is_wgs84=False):
    """
    NDS、WGS84坐标转Tile ID计算
    Parameters
    ----------
    x
    y
    level
    is_wgs84
    
    Author DAKANG
    Returns
    -------

    """
    if is_wgs84:
        nds_x = wgs84_to_nds(x, level)
        nds_y = wgs84_to_nds(y, level, True)
    else:
        nds_x = int(x)
        nds_y = int(y)
    tile_id = (1 << (level + 16))
    # Morton code calculate

    for i in range(level + 1):
        tile_id |= (((nds_x & (1 << i)) >> i) << (2 * i))
        tile_id |= (((nds_y & (1 << i)) >> i) << (2 * i + 1))
    return tile_id

Tile ID 等级解析

C++ 实现

/**
 * 解析 TileId 等级 （0-15级）
 * @param tile_id
 * @return level
 */
int32_t ParseTileLevel(const int32_t tile_id)
{
    int32_t level = 15;
    while (true)
    {
        auto move_bit = level + 16;
        if (((tile_id & (1 << move_bit)) >> move_bit) == 1)
        {
            return level;
        }
        level--;
    }
}

Python 实现

def parse_tile_level(tile_id):
    """
    解析Tile level
    :param tile_id:
    :Author DAKANG
    :return:
    """
    level = 15
    while True:
        move_bit = level + 16
        if ((tile_id & (1 << move_bit)) >> move_bit) == 1:
            return level
        level -= 1

根据Tile ID获取周边相邻的8个Tile ID

C++ 实现

/**
 * 根据Tile Id获取相邻 Tile集合
 * @details 返回该tile的上下左右四个方向的tile 以及四个方向夹角的所有tile
 * @param tile_id
 * @param tiles
 */
void GetAdjacentTiles(const int32_t tile_id, std::vector<int32_t>& tiles)
{
    // 计算 tile 等级
    auto level = ParseTileLevel(tile_id);
    // 定义 nds 横纵坐标
    int32_t x, y;
    ParseTileId(tile_id, x, y);
    // 顺序不可变
    tiles.push_back(EncodeTileId(x - 1, y - 1, level)); // 左上
    tiles.push_back(EncodeTileId(x - 1, y, level)); // 上
    tiles.push_back(EncodeTileId(x - 1, y + 1, level)); // 右上
    tiles.push_back(EncodeTileId(x, y + 1, level)); // 右
    tiles.push_back(EncodeTileId(x + 1, y + 1, level)); // 右下
    tiles.push_back(EncodeTileId(x + 1, y, level)); //下
    tiles.push_back(EncodeTileId(x + 1, y - 1, level)); // 左下
    tiles.push_back(EncodeTileId(x, y - 1, level)); // 左
}

Python 实现

def get_adjacent_tiles(tile_id):
    """
    获取周边8和tile id集合
    :param tile_id:
    :return:
    """
    _tiles = []
    level = parse_tile_level(tile_id)
    nds_x, ndx_y = parse_tile_id_2_nds(tile_id)
    # 顺序不可变
    _tiles.append(encode_tile_id(nds_x - 1, ndx_y - 1, level))  # 左上
    _tiles.append(encode_tile_id(nds_x - 1, ndx_y, level))  # 上
    _tiles.append(encode_tile_id(nds_x - 1, ndx_y + 1, level))  # 右上
    _tiles.append(encode_tile_id(nds_x, ndx_y + 1, level))  # 右
    _tiles.append(encode_tile_id(nds_x + 1, ndx_y + 1, level))  # 右下
    _tiles.append(encode_tile_id(nds_x + 1, ndx_y, level))  # 下
    _tiles.append(encode_tile_id(nds_x + 1, ndx_y - 1, level))  # 左下
    _tiles.append(encode_tile_id(nds_x, ndx_y - 1, level))  # 左
    return _tiles