CH5 无模型控制(Model-free Control)
文章目录
5.1 简介
无模型控制:在未知MDP中通过调整策略优化值函数
可解决的问题:MDP模型未知,尽可以采样得到经验;
MDP模型已知,但是太大了只能进行采样。
On and Off-Policy Learning
- On-Policy learning: 从执行策略 π \pi π所得的采样序列去优化学习策略 π \pi π (边学习边改进自身)
- Off-Policy learning:从执行策略 μ \mu μ所得的采样序列去优化学习策略 π \pi π(观察别人以改进自身)
5.2 On-Policy 蒙特卡洛控制
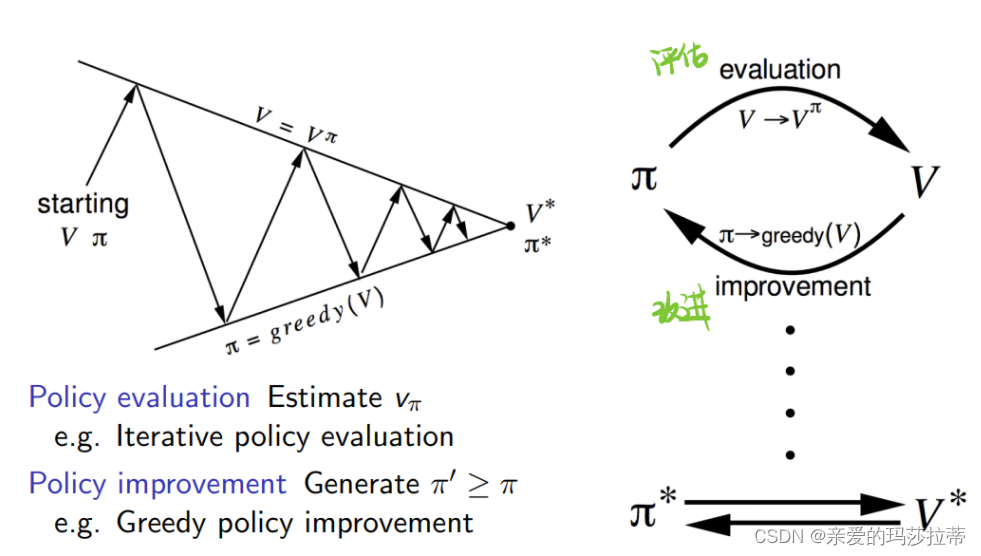
5.2.1 广义策略迭代(Generalised Policy Iteration)
评估策略 π \pi π的值函数,依据此值函数进一步改进策略 π \pi π,再进行评估,直至收敛至最佳
5.2.2 探索
1️⃣贪婪策略探索
基于动作价值函数的贪婪策略改进,选择动作价值函数最大的动作执行,以概率1执行。
π
′
(
s
)
=
a
r
g
m
a
x
a
∈
A
Q
(
s
,
a
)
\pi'(s)=argmax_{a\in A}Q(s,a)
π′(s)=argmaxa∈AQ(s,a)
存在的问题:
- 从初始出现较优者时,策略会一直选择较优者以致于较优者越来越优,有可能错过潜在的更优选择。
- 改进: ϵ − G r e e d y E x p l o r a t i o n \epsilon-Greedy\ Exploration ϵ−Greedy Exploration
2️⃣ ϵ − G r e e d y E x p l o r a t i o n \epsilon-Greedy\ Exploration ϵ−Greedy Exploration
基于动作价值函数的贪婪策略改进,以概率 1 − ϵ 1-\epsilon 1−ϵ执行动作价值函数最大的动作,**以概率 ϵ \epsilon ϵ**选择其他动作。(在策略中加入 ϵ \epsilon ϵ的概率跳出局部最优)
在
m
m
m个动作中,执行动作a的概率是
π
(
a
∣
s
)
=
{
ϵ
/
m
+
1
−
ϵ
i
f
a
∗
=
a
r
g
m
a
x
a
∈
A
Q
(
s
,
a
)
ϵ
/
m
o
t
h
e
r
w
i
s
e
\pi(a|s)=\left\{ \begin{aligned} \epsilon/m+1-\epsilon \ if\ a*=argmax_{a\in A}Q(s,a) \\ \epsilon/m \ otherwise \end{aligned} \right.
π(a∣s)={ϵ/m+1−ϵ if a∗=argmaxa∈AQ(s,a)ϵ/m otherwise
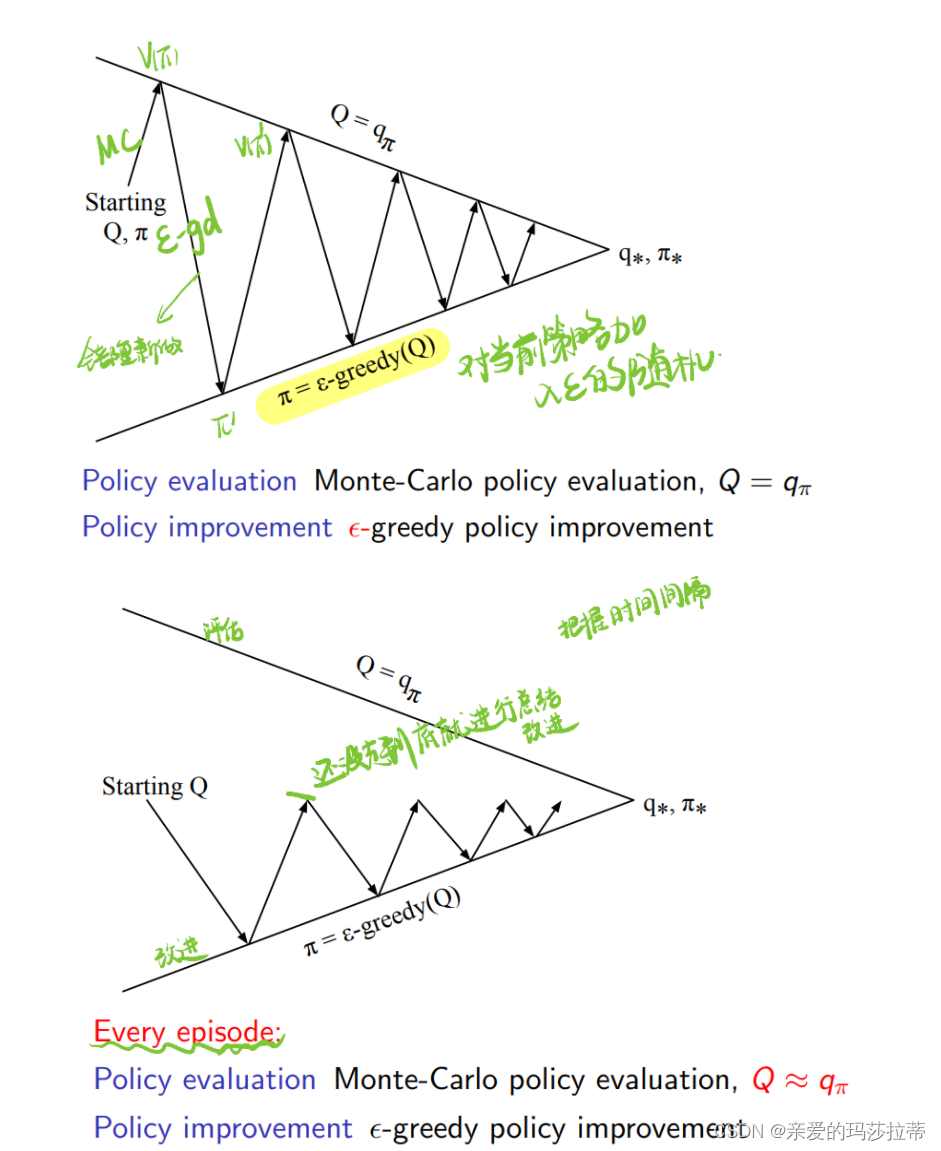
为加快收敛速度,在评估时使用估值,在未完全评估时即进行策略改进。
5.2.3 GLIE
GLIE(Greedy in the limit with infinite exploration):在无限次探索中达到贪婪极限
性质:
- 所有状态-动作对都被无限次探索
l i m k − > ∞ N k ( s , a ) = ∞ \mathop{lim} \limits_{k->\infty}N_k(s,a)=\infty k−>∞limNk(s,a)=∞
- 该策略收敛于普通贪婪策略,即最后以概率1取状态动作值函数最大的动作
l i m k − > ∞ π k ( a ∣ s ) = 1 ( a = a r g m a x a ′ ∈ A Q ( s , a ′ ) ) \mathop{lim} \limits_{k->\infty}{\pi}_k(a|s)=1(a=\mathop{argmax} \limits_{a'\in A}Q(s,a')) k−>∞limπk(a∣s)=1(a=a′∈AargmaxQ(s,a′))
注:只有当 ϵ k = 1 k \epsilon_k=\frac{1}{k} ϵk=k1时, ϵ − G r e e d y E x p l o r a t i o n \epsilon-Greedy\ Exploration ϵ−Greedy Exploration才是 G L I E GLIE GLIE
GLIE蒙特卡洛控制:
第使用策略 π \pi π得到的k个采样序列 S 1 , A 1 , R 2 , . . . , S T {S_1,A_1,R_2,...,S_T} S1,A1,R2,...,ST
对于此序列的每个状态动作对
(
S
t
,
A
t
)
(S_t,A_t)
(St,At):
N
(
S
t
,
A
t
)
<
−
N
(
S
t
,
A
t
)
+
1
Q
(
S
t
,
A
t
)
<
−
Q
(
S
t
,
A
t
)
+
1
N
(
S
t
,
A
t
)
(
G
t
−
Q
(
S
t
,
A
t
)
)
"
增量更新
"
N(S_t,A_t)<-N(S_t,A_t)+1\\ Q(S_t,A_t)<-Q(S_t,A_t)+\frac{1}{N(S_t,A_t)}(G_t-Q(S_t,A_t))\\ "增量更新"
N(St,At)<−N(St,At)+1Q(St,At)<−Q(St,At)+N(St,At)1(Gt−Q(St,At))"增量更新"
基于状态动作值函数改进策略:
ϵ
←
1
/
k
π
←
ϵ
−
g
r
e
e
d
y
(
Q
)
\epsilon \leftarrow 1/k\\ \pi\leftarrow\epsilon-greedy(Q)
ϵ←1/kπ←ϵ−greedy(Q)
注:GLIE蒙特卡洛控制的值函数收敛于最优状态动作值函数
5.3 On-Policy 差分学习
5.3.1 S a r s a ( 0 ) Sarsa(0) Sarsa(0)
状态动作值函数的计算:使用下一状态与下一状态会采取的动作的状态动作值函数(
G
t
G_t
Gt的近似)进行更新(均使用策略
π
\pi
π学习)
Q
(
S
,
A
)
<
−
Q
(
S
,
A
)
+
α
(
R
+
γ
Q
(
S
′
,
A
′
)
−
Q
(
S
t
,
A
t
)
)
Q(S,A)<-Q(S,A)+\alpha(R+\gamma Q(S',A')-Q(S_t,A_t))
Q(S,A)<−Q(S,A)+α(R+γQ(S′,A′)−Q(St,At))
策略(走哪一步)的优化方式: ϵ − g r e e d y ( Q ) \epsilon-greedy(Q) ϵ−greedy(Q)
迭代过程:
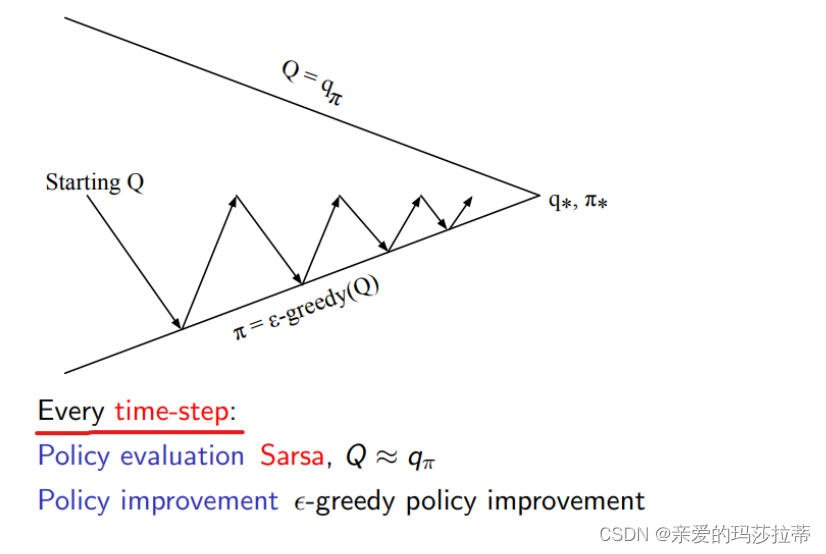

注:Sarsa会收敛到最优动作状态值函数的条件:
- 策略序列为GLIE
- Robbins-Monro 序列的步进尺寸 α t \alpha_t αt:
∑ t = 1 ∞ α t = ∞ ∑ t = 1 ∞ α t 2 = ∞ \sum_{t=1}^{\infty}\alpha_t=\infty\\ \sum_{t=1}^{\infty}\alpha_t^2=\infty t=1∑∞αt=∞t=1∑∞αt2=∞
可以通过设计 α t \alpha_t αt满足上述性质,依次使得动作状态值函数收敛到最优。
5.3.2 S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)
n-Step Sarsa:
状态动作值函数的计算:使用下n个状态与下n个状态会采取的动作的状态动作值函数(
G
t
G_t
Gt的近似)进行更新(均使用策略
π
\pi
π学习)
q
t
(
n
)
=
R
t
+
1
+
γ
R
t
+
2
+
.
.
.
+
γ
n
−
1
R
t
+
n
+
γ
n
Q
(
S
t
+
n
)
Q
(
S
t
,
A
t
)
<
−
Q
(
S
t
,
A
t
)
+
α
(
q
t
(
n
)
−
Q
(
S
t
,
A
t
)
)
q_t^{(n)}=R_{t+1}+\gamma R_{t+2}+...+\gamma^{n-1}R_{t+n}+\gamma ^nQ(S_{t+n})\\ Q(S_t,A_t)<-Q(S_t,A_t)+\alpha(q_t^{(n)}-Q(S_t,A_t))
qt(n)=Rt+1+γRt+2+...+γn−1Rt+n+γnQ(St+n)Q(St,At)<−Q(St,At)+α(qt(n)−Q(St,At))
策略(走哪一步)的优化方式:
ϵ
−
g
r
e
e
d
y
(
Q
)
\epsilon-greedy(Q)
ϵ−greedy(Q)
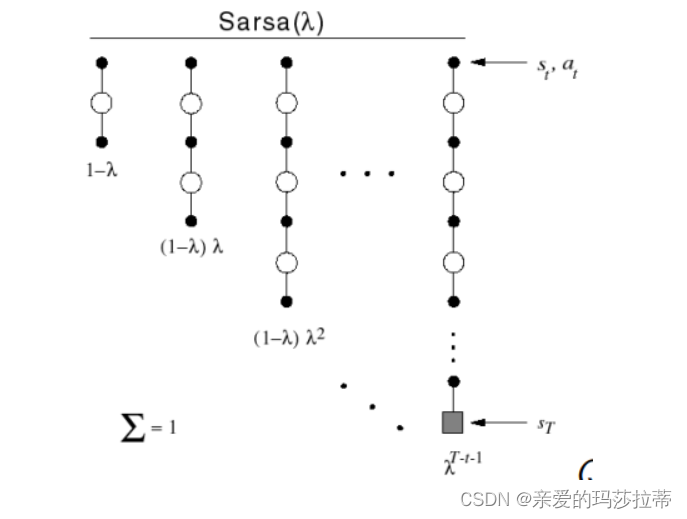
1️⃣前向 S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)
使用权重 ( 1 − λ ) λ n − 1 (1-\lambda)\lambda^{n-1} (1−λ)λn−1组合选择 q t ( n ) q_t^{(n)} qt(n)得到 q λ q^{\lambda} qλ
状态动作值函数的计算:
q
t
λ
=
(
1
−
λ
)
∑
n
=
1
∞
λ
n
−
1
q
t
(
n
)
Q
(
S
t
,
A
t
)
<
−
Q
(
S
t
,
A
t
)
+
α
(
q
t
(
λ
)
−
Q
(
S
t
,
A
t
)
)
q_t^{\lambda}=(1-\lambda)\sum_{n=1}^{\infty}\lambda^{n-1}q_t^{(n)}\\ Q(S_t,A_t)<-Q(S_t,A_t)+\alpha(q_t^{(\lambda)}-Q(S_t,A_t))
qtλ=(1−λ)n=1∑∞λn−1qt(n)Q(St,At)<−Q(St,At)+α(qt(λ)−Q(St,At))
λ
=
1
\lambda=1
λ=1:收敛速度慢,减小
λ
\lambda
λ会缩小收敛速度
2️⃣后向 S a r s a ( λ ) Sarsa(\lambda) Sarsa(λ)
e
l
i
g
i
b
i
l
i
t
y
t
r
a
c
e
eligibility\ trace
eligibility trace
E
0
(
s
,
a
)
=
0
E
t
(
s
,
a
)
=
γ
λ
E
t
−
1
(
s
,
a
)
+
1
(
S
t
=
s
,
A
t
=
a
)
E_0(s,a)=0\\ E_t(s,a)=\gamma\lambda E_{t-1}(s,a)+1(S_t=s,A_t=a)
E0(s,a)=0Et(s,a)=γλEt−1(s,a)+1(St=s,At=a)
Q
(
s
,
a
)
Q(s,a)
Q(s,a)在每个状态s和动作a更新
T
D
−
e
r
r
o
r
:
δ
t
=
R
t
+
1
+
γ
Q
(
S
t
+
1
,
A
t
+
1
−
Q
(
S
t
,
A
t
)
)
Q
(
s
,
a
)
←
Q
(
s
,
a
)
+
α
δ
t
E
t
(
s
,
a
)
TD-error:\delta_t=R_{t+1}+\gamma Q(S_{t+1},A_{t+1}-Q(S_t,A_t))\\ Q(s,a)\leftarrow Q(s,a)+\alpha\delta_tE_t(s,a)
TD−error:δt=Rt+1+γQ(St+1,At+1−Q(St,At))Q(s,a)←Q(s,a)+αδtEt(s,a)

5.4 Off-Policy学习
通过行为策略behavior policy μ ( a ∣ s ) \mu(a|s) μ(a∣s)优化target policy π ( a ∣ s ) \pi(a|s) π(a∣s)
可通过一个策略学到多个策略
5.4.1 Importance Sampling
前述:如何估计不同的分布的期望
E
X
−
P
[
f
(
x
)
]
=
∑
P
(
X
)
f
(
x
)
∑
Q
(
X
)
P
(
X
)
Q
(
X
)
f
(
X
)
=
E
X
−
Q
[
P
(
X
)
Q
(
X
)
f
(
X
)
]
E_{X-P}[f(x)]=\sum P(X)f(x)\\ \sum Q(X)\frac{P(X)}{Q(X)}f(X)\\ =E_{X-Q}[\frac{P(X)}{Q(X)}f(X)]
EX−P[f(x)]=∑P(X)f(x)∑Q(X)Q(X)P(X)f(X)=EX−Q[Q(X)P(X)f(X)]
1️⃣Importance Sampling for Off-Policy Monte-Carlo
使用 μ \mu μ的回报估计 π \pi π
基于策略间的相似性求取权重回报
G
t
G_t
Gt,需要多次采样
G
t
π
/
μ
=
π
(
A
t
∣
S
t
)
π
(
A
t
+
1
∣
S
t
+
1
)
.
.
.
π
(
A
T
∣
S
T
)
μ
(
A
t
∣
S
t
)
μ
(
A
t
+
1
∣
S
t
+
1
)
.
.
.
μ
(
A
T
∣
S
T
)
G
t
π
与
μ
越接近,
G
t
π
/
μ
越接近
G
t
G_t^{\pi / \mu}=\frac{\pi(A_t|S_t)\pi(A_{t+1}|S_{t+1})...\pi(A_{T}|S_{T})}{\mu(A_t|S_t)\mu(A_{t+1}|S_{t+1})...\mu(A_{T}|S_{T})}G_t\\ \pi与\mu越接近,G_t^{\pi / \mu}越接近G_t
Gtπ/μ=μ(At∣St)μ(At+1∣St+1)...μ(AT∣ST)π(At∣St)π(At+1∣St+1)...π(AT∣ST)Gtπ与μ越接近,Gtπ/μ越接近Gt
值函数的更新:
V
(
S
t
)
←
V
(
S
t
)
+
α
(
G
t
π
/
μ
−
V
(
S
t
)
)
V(S_t)\leftarrow V(S_t)+\alpha(G_t^{\pi / \mu}-V(S_t))
V(St)←V(St)+α(Gtπ/μ−V(St))
Importance Sampling mc 具有较大方差。
2️⃣Importance Sampling for Off-Policy TD
使用 μ \mu μ的TD targets估计 π \pi π
只需要一次采样
值函数的更新:
V
(
S
t
)
←
V
(
S
t
)
+
α
(
π
(
A
t
∣
S
t
)
μ
(
A
t
∣
S
t
)
(
R
t
+
1
+
γ
V
(
S
t
+
1
)
−
V
(
S
t
)
)
V(S_t)\leftarrow V(S_t)+\alpha(\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}(R_{t+1}+\gamma V(S_{t+1})-V(S_t))
V(St)←V(St)+α(μ(At∣St)π(At∣St)(Rt+1+γV(St+1)−V(St))
TD Importance Sampling的方差比MC 小。
5.4.2 Q-learning
状态动作值函数的计算:
依据行为策略
μ
\mu
μ选择下一动作,考虑target 策略
π
\pi
π的下一个备选动作的值函数
Q
(
S
t
,
A
t
)
<
−
Q
(
S
t
,
A
t
)
+
α
(
R
t
+
1
+
γ
Q
(
S
t
+
1
,
A
′
)
−
Q
(
S
t
,
A
t
)
)
Q(S_t,A_t)<-Q(S_t,A_t)+\alpha(R_{t+1}+\gamma Q(S_{t+1},A')-Q(S_t,A_t))
Q(St,At)<−Q(St,At)+α(Rt+1+γQ(St+1,A′)−Q(St,At))
策略(走哪一步)的优化方式: g r e e d y ( Q ) greedy(Q) greedy(Q)
学习收敛过程:
- target策略 π \pi π采用 G r e e d y Greedy Greedy策略改进:
π ( S t + 1 ) = a r g m a x a ′ Q ( S t + 1 , a ′ ) \pi(S_{t+1})=argmax_{a'}Q(S_{t+1},a') π(St+1)=argmaxa′Q(St+1,a′)
- 行为策略 μ \mu μ采用 ϵ − G r e e d y \epsilon-Greedy ϵ−Greedy策略改进
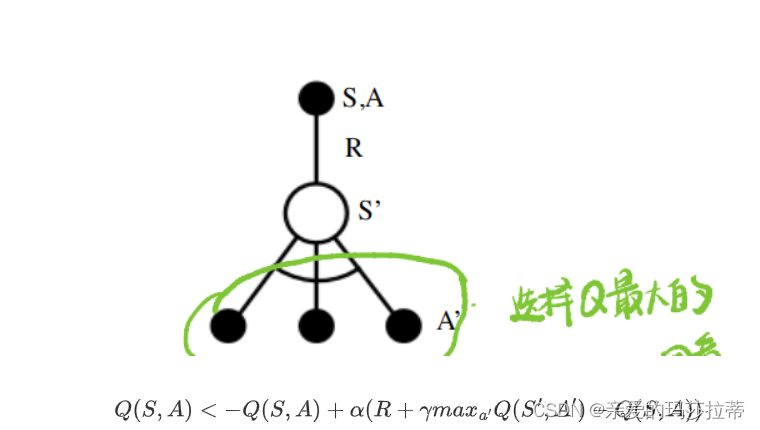
Q
(
S
,
A
)
<
−
Q
(
S
,
A
)
+
α
(
R
+
γ
m
a
x
a
′
Q
(
S
′
,
A
′
)
−
Q
(
S
,
A
)
)
Q(S,A)<-Q(S,A)+\alpha(R+\gamma max_{a'}Q(S',A')-Q(S,A))
Q(S,A)<−Q(S,A)+α(R+γmaxa′Q(S′,A′)−Q(S,A))
在所有的可能的A’中,选择Q(S’,A’)最大的进行运算。
注:Q-learning的值函数收敛于最优状态动作值函数。
例:Cliff Walking Example
在4*12的棋盘格中,个体从S出发,目标为G,动作为上下左右,到达空白格的奖励R=-1,到达“The Cliff”带的奖励R=-100,其中到达“The Cliff"带的个体会返回起点S。问:safe path 和 optimal path 的路径分别是什么方法学习的?
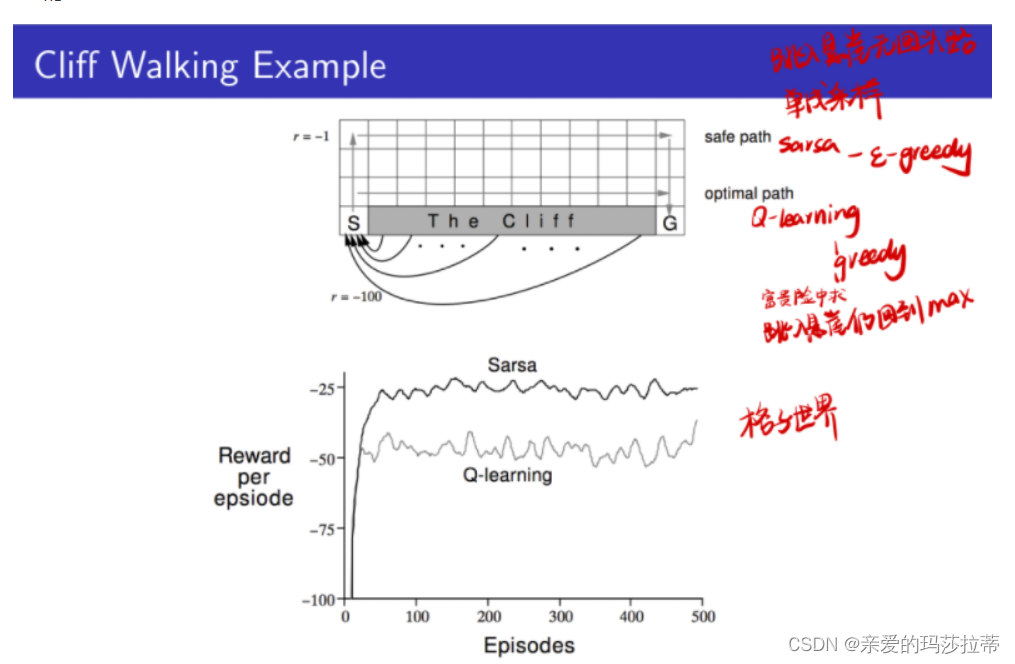
答:safe path 是sarsa学习的,optimal path 是Q-learning算法学习的。
因为Q-learning是采用绝对Greedy算法改进Target policy的,倾向于最优选择,而Sarsa是采用 ϵ − G r e e d y \epsilon-Greedy ϵ−Greedy策略,有一定几率采取其他动作。
还因为Q-learning是选择Q值最优的动作执行,而Sarsa是只有一个动作的,没有退回的余地。
5.5对比分析
什么函数 什么更新方法
进行了什么近似处理
最后会不会收敛到最优






















 5314
5314











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








