灰度变换-习题

题1

（a）试求出实现示于下图的对比度展宽变换的连续函数。此函数不仅包含参数m，而且还包括参数E，以便于控制灰度值由低向高转化时的函数斜率。该函数应归一化，以使它的最小值和最大值分别为0和1

答：
$$s=T\left(r\right)=\frac{1}{1+{\left(m/r\right)}^E}$$
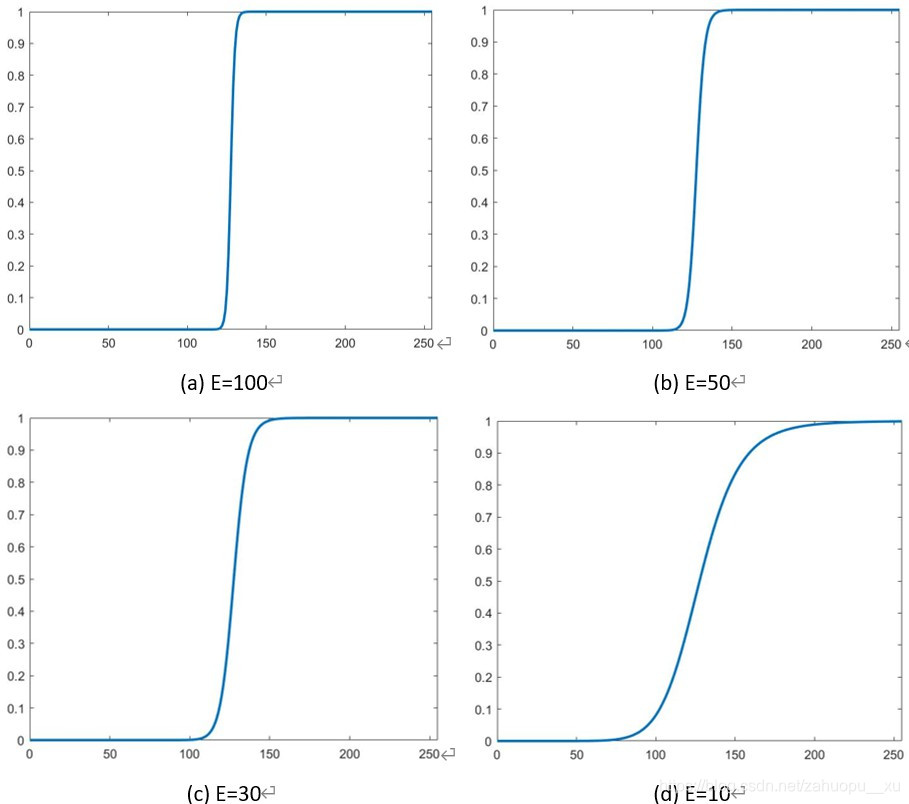
（b）作为参数E的函数，设计一组变换，m值固定为L/2，L是图像中灰度的级数
答：

题2

一幅8灰度级图像具有如下所示的直方图，求直方图均衡后的灰度级和对应概率，并画出均衡后的直方图的示意图。（图中的8个不同灰度级对应的归一化直方图为[0.17 0.25 0.21 0.16 0.07 0.08 0.04 0.02]）

答：

由此可以推得，新的灰度级为

且

由此绘得新的直方图：

题3

一幅图像的灰度PDF，$p_r\left(r\right)$示于下图。先对此图进行灰度变换，使其灰度表达式为下面右图的$p_z\left(z\right)$。假设灰度值连续，求完成这一要求的变换（r到z）。

答：
先对$p_r\left(r\right)$做直方图均衡化：
$$s=T\left(r\right)={\int }_0^r\left(-2w+2\right)dw=-r^2+2r$$
再对$p_z\left(z\right)$做直方图均衡化：
$$H\left(z\right)={\int }_0^z\left(2w\right)dw=z^2$$
可以得到：
$$z=\pm \sqrt{H\left(z\right)}$$
由于灰度值只能为正，则：
$$z=\sqrt{H\left(z\right)}$$
将$H\left(z\right)$替换成$s$：
$$z=\sqrt{-r^2+2r}$$