[秩相关] Spearman秩相关系数计算及假设检验

首先说明秩相关系数还有其他类型，比如kendal秩相关系数。

使用Pearson线性相关系数有2个局限：

1. 必须假设数据是成对地从正态分布中取得的。
2. 数据至少在逻辑范围内是等距的。

对于更一般的情况有其他的一些解决方案，Spearman秩相关系数就是其中一种。Spearman秩相关系数是一种无参数（与分布无关）检验方法，用于度量变量之间联系的强弱。在没有重复数据的情况下，如果一个变量是另外一个变量的严格单调函数，则Spearman秩相关系数就是+1或-1，称变量完全Spearman秩相关。注意这和Pearson完全相关的区别，只有当两变量存在线性关系时，Pearson相关系数才为+1或-1。

对原始数据x_i,y_i按从大到小排序，记x'_i,y'_i为原始x_i,y_i在排序后列表中的位置，x'_i,y'_i称为x_i,y_i的秩次，秩次差d_i=x'_i-y'_i。Spearman秩相关系数为：

           

位置	原始X	排序后	秩次	原始Y	排序后	秩次	秩次差
1	12	546	5	1	78	6	1
2	546	45	1	78	46	1	0
3	13	32	4	2	45	5	1
4	45	13	2	46	6	2	0
5	32	12	3	6	2	4	1
6	2	2	6	45	1	3	-3

对于上表数据，算出Spearman秩相关系数为：1-6*(1+1+1+9)/(6*35)=0.6571

如果原始数据中有重复值，则在求秩次时要以它们的平均值为准，比如：

原始X	秩次	调整后的秩次
0.8	5	5
1.2	4	(4+3)/2=3.5
1.2	3	(4+3)/2=3.5
2.3	2	2
18	1	1

假设检验：

Spearman秩相关系数也应该进行假设检验，当n小于等于50时，用查表法，当n大于50时，计算统计量t的值，即用前面皮尔森相关系数假设检验中t值的计算方式。

对于上述数据，查阅秩相关系数检验的临界值表

n	显著水平
	0.05	0.01
5	0.9	1
6	0.829	0.943
7	0.714	0.893

置信度=1-显著水平。上表显示在n=6的时候，当spearman秩相关系数>=0.829时我们有95%的置信度认为两个随机变量相关，当spearman秩相关系数>=0.943时我们有99%的置信度认为两个随机变量相关。由于0.6571<0.829，即置信度达不到95%，所以我们不能认为X和Y相关。

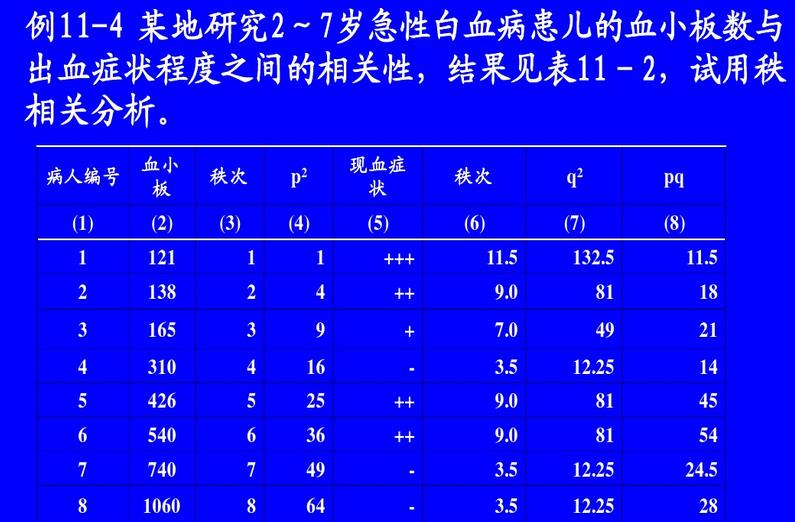
实例：