monte carlo simulation

$\textbf{1.连续状态马尔科夫链}$

$\quad\quad$我们默认本文中的马尔科夫链都是离散时间的。通常，我们所见到的马尔科夫链是离散状态的，但是为了能够模拟出连续随机变量的样本，我们必须引入连续状态马尔科夫链。通常，一个马尔科夫链由初始分布和状态转移矩阵来决定，相似的，连续状态马尔科夫链也是由这两个因素构成，只不过状态转移矩阵没办法来描述连续状态，我们再次引入转移核的概念，转移矩阵描述的是条件概率，同样，转移核描述的是条件概率，假设在$t$时刻状态值为$x_t$,那么在$t+1$时刻的状态的概率密度函数为$K(x_t,x_{t+1})$,所以

$$K(x_t,A)=\int_AK(x_t,x_{t+1})dx_{t+1}$$
通常写成 $\int_AK(x_t,dx_{t+1})$,表示t+1时刻状态为A的条件概率。
同样，引出给定初始状态 $x_0$,不同时刻状态的联合分布为
$$P(x_1 \in A_1,...,x_n \in A_n|x_0)=\int_{A_1}...\int_{A_n}K(x_{n-1},x_n)...K(x_0,x_1)$$
这和离散状态是相似的。
同样给出chapman-Kolmogorov 方程.目的就是给出n阶转移核，和离散状态n阶转移矩阵相似。For every (m,n) $\in$ $N^2$，
$$K^{m+n}(x,A)=\int_{y \in Y}K^n(y,A)K^m(x,dy)$$
最后我们给出连续状态马尔科夫链的平稳分布和 $\textbf{detailed balance condition}$的关系，这和MCMC联系紧密。
$\textbf{平稳分布.}$不同时刻的状态分布相同，都为 $\pi$,这个 $\pi$就是平稳分布
$\textbf{detailed balance condition.}$一个马尔科夫链，其转移核为K满足detailed balanced condition，即存在函数 $f(x)$
$$K(y,x)f(y)=K(x,y)f(x)$$
对每一个 $(x,y)$成立
$\color{red}{如何一个概率密度函数\pi使得马尔科夫链的转移核满足}$
$\color{red}{detailed balanced condition}$，
$\color{red}{那么这个概率密度函数\pi就是该马尔科夫链的平稳分布。}$
(靠，写了半天，只有这个有用。。，但是。。还没完，我靠了。。。不写了，不是很影响，在下面的metropolis-hastings算法中，我会说明如何构造相关的量的)

$\textbf{2.MCMC method for simulation.}$引用monte carlo statistical method【点这里】中的定义7.1.
$\quad\quad$Markov chain Monte Carlo method for the simulation of distribution $f$ is ay method producing an ergodic markov chain ($X^{(t)}$) whose stationary distribution is $f$.
$\quad\quad$核心在于产生一个markov chain 使得我们需要模拟的分布是这个markov chain 的平稳分布，同时是遍历各态的，这样，我们就可以根据分布函数$f$进行抽样了。
$\textbf{3.metropolis hastings method.}$
Given $x^{(t)}$,
1.Generate $Y_t \sim q(y|x^{(t)}).$
2.Take
$\quad\quad$ $X^{(t+1)} =Y_t$ with probability $\rho(x^{(t)},Y_t)$
$\quad\quad$$X^{(t+1)}=X^{(t)}$ with probability 1-$\rho(x^{(t)},Y_t)$
where
$\rho(x,y)=min\{ \frac {f(y)}{f(x)} \frac {q(x|y)}{q(y|x)},1 \}$

the distribution q is called the instrumental distribution and the probability $\rho(x,y)$ the metropolis-hastings acceptance proability.
结论：如果算法中的$q(y|x)$满足如下两个条件

$$P[f(x^{(t)})q(Y_t|x^{(t)}) \leq f(Y_t)q(x^{(t)}|Y_t)] < 1$$
$$q(y|x) > 0$$
那么如果 $h \in L^1(f)$,那么
$$\lim_{T \rightarrow \infty} \frac{1}{T} \sum_{t=1}^T h(X^{(t)})=\int h(x)f(x)dx$$
$$\lim_{n \rightarrow \infty}|| \int K^n(x,.)\mu(dx)-f||=0$$
$\mu$是初始状态分布。
$\textbf{4.gibbs抽样.}$
如果我们已知 $X={x_1,x_2,...,x_D}$的联合分布 $f(X)$,我们想要得到 $X$的样本，我们可以用gibbs抽样的方法来得到关于$x_1$的样本，具体的过程如下

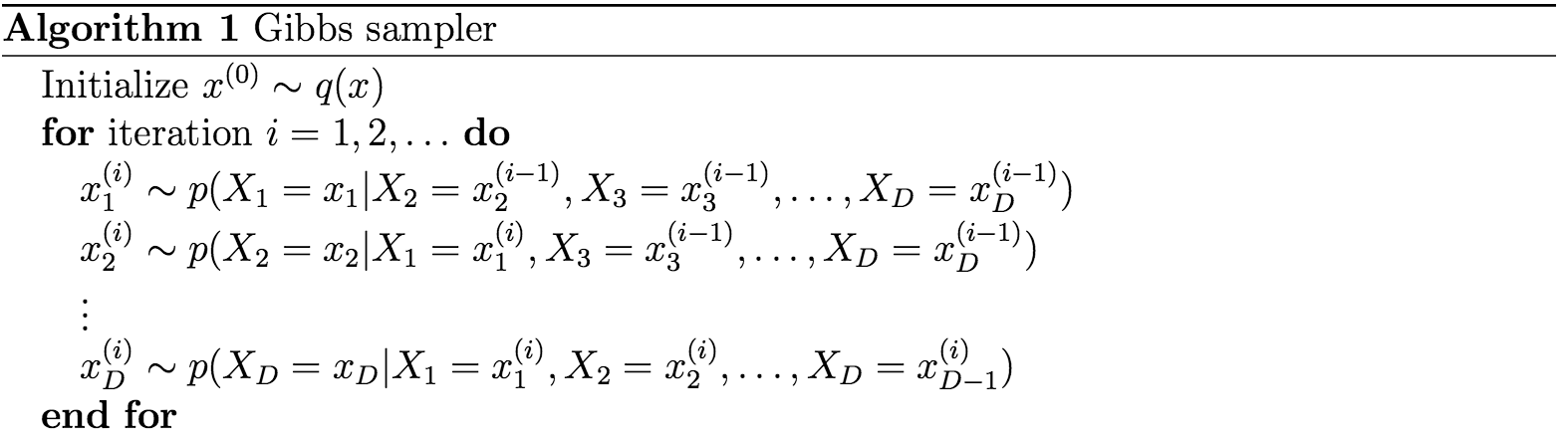
关键在于条件分布的抽样确定
我们可以用下式来
$p(X_1=x_1|X_2=x_2^{(i-1)},...,X_D=x_D^{(i-1)})=\frac{p(X_1=x_1,X_2=x_2^{(i-1)},...X_D=x_D^{(i-1)})}{p(X_2=x_2^{i-1},...,X_D=x_D^{(i-1)})}$
上式的右边的分母是一个标准化的东西，跟 $X_1$无关，所以这个条件分布是和 $p(X_1=x_1,X_2=x_2^{(i-1)},...X_D=x_D^{(i-1)})$呈正比，所以，我们在对这个条件概率抽样的时候，是可以不用担心分布这一项的，抽样是不会用到这一项的