圆周对称点

虽然小标题很多，但里面的内容不多，慢慢看！

一、背景简介

  考虑这样一个问题：已知圆 $O$ 内一点 $M_0,O{M}_0={\rho }_0$，求射线 $O{M}_0$ 上一点 $M_1$，使得对于圆周上任一点 $P$，都有 $P{M}_0/P{M}_1$ 为常数.

二、求解思路

  “听起来不可思议，去做做才知道有没有可能”.
  设 $OP$ 与极轴的夹角为 $\theta ,O{M}_1=d$，则$$P{M}_0^2=R^2+{\rho }_0^2-2R{\rho }_{0}cos\theta$$$$P{M}_1^2=R^2+d^2-2Rdcos\theta$$记$$g(\theta )=\frac{P{M}_0^2}{P{M}_1^2}=\frac{R^2+{\rho }_0^2-2R{\rho }_{0}cos\theta }{R^2+d^2-2Rdcos\theta }$$根据题意，$g(\theta )$ 的值应与 $P$ 的位置无关，即 $$\frac{dg(\theta )}{d\theta }=0$$$$\frac{dg(\theta )}{d\theta }=\frac{2R{\rho }_{0}sin\theta }{P{M}_1^4}(d^2-\frac{R^2+{\rho }_0^2}{{\rho }_0}d+R^2)=0$$则$$d^2-\frac{R^2+{\rho }_0^2}{{\rho }_0}d+R^2=0$$解得$$d=\frac{R^2}{{\rho }_0}or{\rho }_0.$$故取 $O{M}_1=R^2/{\rho }_0,P{M}_0/P{M}_1={\rho }_0/R$，并将 $M_1$ 称为 $M_0$ 关于圆周的对称点.

三、小动画欣赏

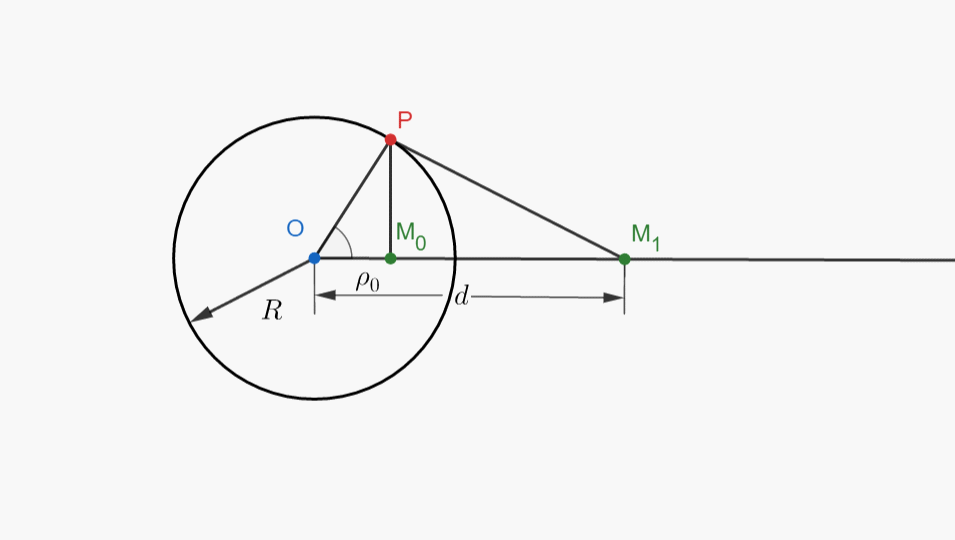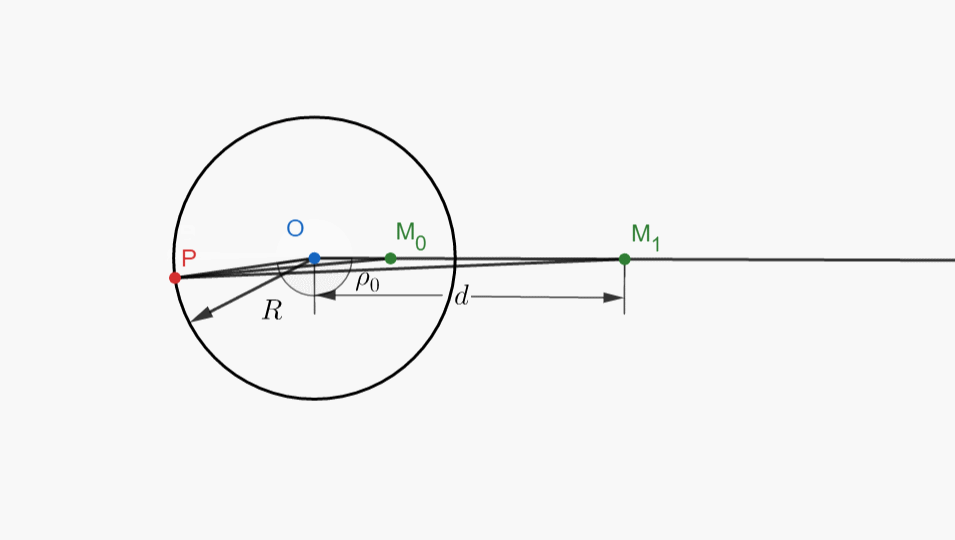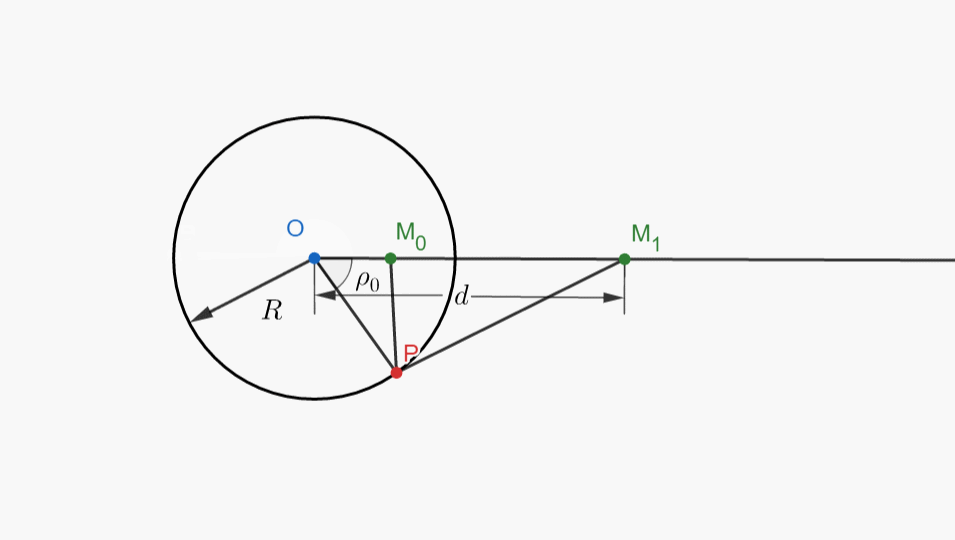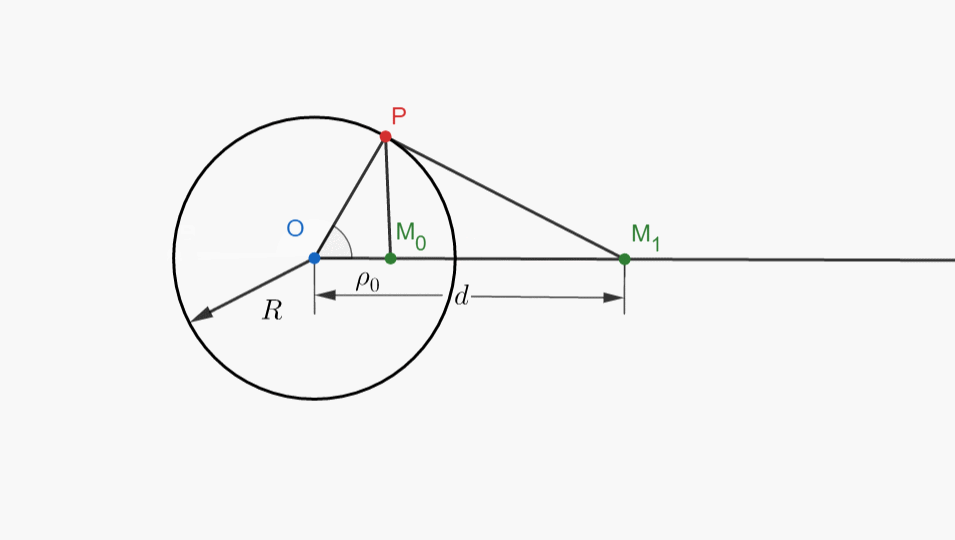
四、思维倒置

  假设已知 $O{M}_1=R^2/{\rho }_0$，则对于圆周上任意一点 $P$，都有$$\frac{OP}{O{M}_0}=\frac{O{M}_1}{OP}$$又 $\because \angle M_{0}OP=\angle PO{M}_1$
$$\therefore \Delta M_{0}OP\sim \Delta PO{M}_1$$$$\frac{P{M}_0}{P{M}_1}=\frac{O{M}_0}{OP}=\frac{{\rho }_0}{R}=C$$

五、几何做法

虽然 $O{M}_1$可以以 $R^2/{\rho }_0$的方式表示出来，但能否通过简单的几何方法做出来呢？答案是肯定的，做法如下：

1. 首先过 $M_0$ 点作 $O{M}_0$ 的垂线与圆交于点 $P$；
2. 连接 $OP$，作 $OP$ 的垂线与射线 $O{M}_0$ 交于点 $M_1$；

则点 $M_1$ 满足 $O{M}_1=R^2/{\rho }_0$，证明如下：
$$\begin{array}{rl}& \because \angle M_{0}OP=\angle PO{M}_1,\angle O{M}_{0}P=\angle OP{M}_1=\frac{\pi }{2}\\ & \therefore \Delta M_{0}OP\sim \Delta PO{M}_1\\ & \therefore \frac{O{M}_1}{OP}=\frac{OP}{O{M}_0},O{M}_1=\frac{O{P}^2}{O{M}_0}=\frac{R^2}{{\rho }_0}\end{array}$$

六、从另一角度出发

圆周对称点的另一种表现形式 $or$ 充要条件：
若过 $M_0,M_1$ 的任意圆周均与圆 $O$ 正交，即两个圆心和交点所成角为直角，则称 $M_0,M_1$ 互为 关于圆 $O$ 的对称点.
分析： 由于过这两点的任意圆周都与圆 $O$ 有交点且不与$M_0,M_1$ 共线，所以可以通过 $M_0,M_1$ 以及圆 $O$ 上任一点 $P$ 来确定经过 $M_0,M_1$ 的圆周，其中 $P$ 不与 $M_0,M_1$ 共线.

证明过程如下：
充分性($⟸$)：
  已知对圆 $O$ 上任一点 $P$，都有经过 $M_0,M_1,P$ 的圆 $O^{\prime }$ 与圆 $O$ 正交，即 $\angle OP{O}^{\prime }=\pi /2$，证明 $M_1$ 为 $M_0$ 关于圆 $O$ 的对称点，根据前面的讨论，只需证$\Delta M_{0}OP\sim \Delta PO{M}_1$ 即可.
  因为 $\angle OP{M}_0$ 为弦切角，$\angle O{M}_{1}P$ 为圆弧 $\overgroup{P{M}_0}$ 对应的圆周角，由弦切角定理可知二者相等，又因为 $\angle M_{0}OP=\angle PO{M}_1$，所以 $\Delta M_{0}OP\sim \Delta PO{M}_1$.
必要性($⟹$)：
  已知 $M_1$ 为 $M_0$ 关于圆 $O$ 的对称点，所以对圆 $O$ 上任一点 $P$，都有 $\Delta M_{0}OP\sim \Delta PO{M}_1$，所以有 $\angle OP{M}_0=\angle O{M}_{1}P$，又因为 $\angle O^{\prime }P{M}_0+\angle O{M}_{1}P=\pi /2$，所以 $\angle O^{\prime }P{M}_0+\angle OP{M}_0=\angle O^{\prime }PO=\pi /2,OP\perp P{O}^{\prime }$，故有：过 $M_0,M_1$ 的任意圆周均与圆 $O$ 正交.

七、应用

1. 已知接地金属球壳内部有一点电荷 $q$，距球心距离为 $d$，求球壳内部电势分布.
   解法: 易知球壳上电势为零，在 $q$ 关于球壳的对称点(求法与圆周对称点完全相同)处放置电量为 $Rq/{\rho }_0$ 的负电荷，将球壳拿掉，则球壳处电势为零，球壳内部电势不变(证明参照数理方程之 $Laplace$ 方程第一边值问题解的唯一性)；
2. 求球域或圆域上 $Laplace$ 方程第一边值问题的 $Green$ 函数.

八、补充

1. 取 $P$ 为线段 $M_0{M}_1$ 与圆的交点，则$$O{M}_0\cdot O{M}_1=(OP-P{M}_0)(OP+P{M}_1)=O{P}^2$$$$(R-P{M}_0)(R+P{M}_1)=R^2$$解得$$P{M}_1-P{M}_0=\frac{P{M}_1\cdot P{M}_0}{R}$$当圆的半径 $R\to \infty$ 时，圆退化为直线，$P{M}_1=P{M}_0$，关于圆周的对称点退化为关于直线的对称点；

2. 反向思维
   根据上述讨论，圆周上的点到一对对称点的距离之比为常数，反过来呢，到两个定点的距离之比为定值的动点会形成怎样的轨迹？很容易猜得答案是圆.
   最先思考这个问题的是古希腊数学家阿波罗尼斯，所以这种圆也被称为
   Apollonian_circle(阿波罗尼斯圆)
   证明思路很简单，利用直角坐标系：设 $A$ 的坐标为 $(0,0)$，$B$ 的坐标为 $(a,0)$，设 $P$ 的坐标为 $(x,y)$，根据 $|PA|/|PB|=\lambda ,|PA{|}^2/|PB{|}^2={\lambda }^2$，即 $(x^2+y^2)/[(x-a{)}^2+y^2]={\lambda }^2$. 整理可得：$[x-{\lambda }^{2}a/({\lambda }^2-1){]}^2+y^2=[\lambda a/({\lambda }^2-1){]}^2$，即动点 $P$ 的轨迹为一个以 $({\lambda }^{2}a/({\lambda }^2-1),0)$ 为圆心、$\lambda a/({\lambda }^2–1)$ 为半径的圆。当 $\lambda >1$ 时，圆心在 $B$ 点的右侧；当 $\lambda <1$ 时，圆心在 $A$ 点的左侧。特别地，当 $\lambda =1$ 时，圆心位于无穷远，半径无穷大，此时阿波罗尼斯圆变成了线段 $AB$ 的中垂线.

九、总结

$M_0$ 关于圆周的对称点 $M_1$ 的三种打开方式：

1. 对于圆周 $O$ 上任一点 $P$，都有 $P{M}_0/P{M}_1$ 为常数，可求得该常数为 $O{M}_0/R$;
2. 对于圆周 $O$ 上任一点 $P$，都有 $\Delta M_{0}OP\sim \Delta PO{M}_1$；
3. 过 $M_0,M_1$ 的任意圆周均与圆 $O$ 正交.

Plus: 如有错误、可以改进的地方、或任何想说的，请在评论区留言！