前言
介绍数据速率、码片速率、符号速率,以及连续频率信号持续时间和符号持续时间的计算计算方式。
参考资料《LoRa速率》
一、码片速率
BW的单位是Hz,带宽BW和码片速率的转换关系:
B
W
=
R
c
=
c
h
i
p
r
a
t
e
(
c
h
i
p
s
/
s
)
BW=R_c=chip rate(chips/s)
BW=Rc=chiprate(chips/s)
举例:
B
W
=
125
k
H
z
BW=125kHz
BW=125kHz
B
W
=
R
c
=
125000
(
c
h
i
p
s
/
s
)
BW=R_c=125000 (chips/s)
BW=Rc=125000(chips/s)

二、符号速率
- 符合速率的计算过程:
R s ( s y m b o l s / s e c ) = B W / 2 S F = R c / 2 S F R_s(symbols/sec)=BW / 2^{SF} = R_c / 2^{SF} Rs(symbols/sec)=BW/2SF=Rc/2SF - 举例:
B
W
=
125
k
H
z
,
S
F
=
7
BW=125kHz,SF=7
BW=125kHz,SF=7
B W = 125000 / 2 7 = 977 s y m b o l s / s e c BW=125000/2^7=977symbols/sec BW=125000/27=977symbols/sec

三、数据速率
-
码片速率总是高于符号速率: R c > R s R_c>R_s Rc>Rs
-
比特速率计算过程:
R b ( b i t s / s e c ) = S F × B W 2 S F × 4 4 + C R R_b(bits/sec)=SF \times {\frac{BW}{2^{SF}}\times{\frac{4}{4+CR}}} Rb(bits/sec)=SF×2SFBW×4+CR4
SF:7 - 12
CR:1 - 4 -
举例:SF=7,CR=1
B W = 125 k H z , R b = 7 × ( 125000 / 2 7 ) × ( 4 / ( 4 + 1 ) ) = 5.5 k b p s BW=125kHz,R_b=7 \times (125000 / 2^7) \times (4 / (4+1))=5.5kbps BW=125kHz,Rb=7×(125000/27)×(4/(4+1))=5.5kbps
B W = 250 k H z , R b = 7 × ( 250000 / 2 7 ) × ( 4 / ( 4 + 1 ) ) = 10.9 k b p s BW=250kHz,R_b=7 \times (250000 / 2^7) \times (4 / (4+1))=10.9kbps BW=250kHz,Rb=7×(250000/27)×(4/(4+1))=10.9kbps
B W = 500 k H z , R b = 7 × ( 500000 / 2 7 ) × ( 4 / ( 4 + 1 ) ) = 21.9 k b p s BW=500kHz,R_b=7 \times (500000 / 2^7) \times (4 / (4+1))=21.9kbps BW=500kHz,Rb=7×(500000/27)×(4/(4+1))=21.9kbps
- 如果提高带宽,比特速率或者数据速率也会提高。
- 如果提高扩频因子,比特速率或者数据速率也会提高。
- 举例:BW=125kHz,CR=1
S F = 7 , R b = 7 × ( 125000 / 2 7 ) × ( 4 / ( 4 + 1 ) ) = 5.5 k b p s SF=7,R_b=7 \times (125000 / 2^7) \times (4 / (4+1))=5.5kbps SF=7,Rb=7×(125000/27)×(4/(4+1))=5.5kbps
S F = 8 , R b = 7 × ( 125000 / 2 8 ) × ( 4 / ( 4 + 1 ) ) = 3.13 k b p s SF=8,R_b=7 \times (125000 / 2^8) \times (4 / (4+1))=3.13kbps SF=8,Rb=7×(125000/28)×(4/(4+1))=3.13kbps
S F = 9 , R b = 7 × ( 125000 / 2 9 ) × ( 4 / ( 4 + 1 ) ) = 1.76 k b p s SF=9,R_b=7 \times (125000 / 2^9) \times (4 / (4+1))=1.76kbps SF=9,Rb=7×(125000/29)×(4/(4+1))=1.76kbps
S F = 10 , R b = 7 × ( 125000 / 2 1 0 ) × ( 4 / ( 4 + 1 ) ) = 0.98 k b p s SF=10,R_b=7 \times (125000 / 2^10) \times (4 / (4+1))=0.98kbps SF=10,Rb=7×(125000/210)×(4/(4+1))=0.98kbps
S F = 11 , R b = 11 × ( 125000 / 2 1 1 ) × ( 4 / ( 4 + 1 ) ) = 0.54 k b p s SF=11,R_b=11 \times (125000 / 2^11) \times (4 / (4+1))=0.54kbps SF=11,Rb=11×(125000/211)×(4/(4+1))=0.54kbps
S F = 12 , R b = 12 × ( 125000 / 2 1 2 ) × ( 4 / ( 4 + 1 ) ) = 0.29 k b p s SF=12,R_b=12 \times (125000 / 2^12) \times (4 / (4+1))=0.29kbps SF=12,Rb=12×(125000/212)×(4/(4+1))=0.29kbps
四、码片传输时间
- 因为
R
c
=
B
W
R_c=BW
Rc=BW,码片传输时间:
T c ( s e c ) = 1 / B W T_c(sec)=1/BW Tc(sec)=1/BW - 举例:BW=125kHz
T c = 1 / 125000 = 8 u s T_c = 1/125000 = 8us Tc=1/125000=8us
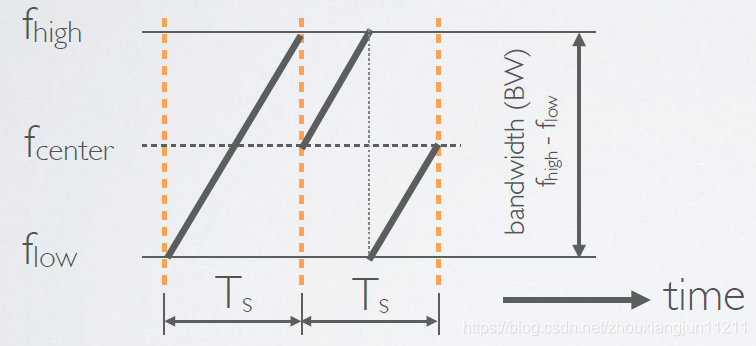
五、符号传输时间
- 符号传输时间或者扫描时间计算过程:
T s ( s e c ) = 2 S F / B W T_s(sec)=2^{SF}/BW Ts(sec)=2SF/BW
SF:7 -12
- 举例:SF 7
B W = 125 k H z , T s = 2 7 / 125000 = 1.024 m s BW=125kHz,T_s=2^{7}/125000=1.024ms BW=125kHz,Ts=27/125000=1.024ms
B W = 250 k H z , T s = 2 7 / 250000 = 512 m s BW=250kHz,T_s=2^{7}/250000=512ms BW=250kHz,Ts=27/250000=512ms
B W = 500 k H z , T s = 2 7 / 500000 = 256 m s BW=500kHz,T_s=2^{7}/500000=256ms BW=500kHz,Ts=27/500000=256ms
- 举例:BW=125kHz
S F = 7 , T s = 2 7 / 125000 = 1.024 m s SF=7,T_s=2^{7}/125000=1.024ms SF=7,Ts=27/125000=1.024ms
S F = 9 , T s = 2 9 / 125000 = 4.096 m s SF=9,T_s=2^{9}/125000=4.096ms SF=9,Ts=29/125000=4.096ms
S F = 12 , T s = 2 12 / 125000 = 32.768 m s SF=12,T_s=2^{12}/125000=32.768ms SF=12,Ts=212/125000=32.768ms
六、扩频因子对波形的影响
固定带宽,不同扩频因子如下图:

- 扩频因子加1,符号传输时间或扫描时间翻倍;
- 当信号微弱时或者干扰强时,LORA设备提高扩频因子;
- 如果终端设备与网关设备距离较远时,需要使用高扩频因子;








 本文介绍了扩频技术中的关键概念,包括码片速率、符号速率、数据速率及其计算方法,并探讨了扩频因子对波形的影响。
本文介绍了扩频技术中的关键概念,包括码片速率、符号速率、数据速率及其计算方法,并探讨了扩频因子对波形的影响。
















 1037
1037

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








