高等数学笔记(上下)

不定积分

第一类换元积分法：灵感来自于复合函数的求导，利用中间变量替换得到复合函数的积分法：设$f(u)$具有原函数，$u=\phi (x)$可导，则有换元公式
$$\int f[\phi (x)]{\phi }^{\prime }(x)dx=[\int f(u)du{]}_{u=\phi (x)}$$
$$\int 2\cos 2xdx=\int \cos 2x(2x{)}^{\prime }dx(令u=2x)=\sin 2x+C$$
$$\int 2x{e}^{x^2}dx=\int e^{x^2}(x^2{)}^{\prime }dx=e^{x^2}+C$$
第二类换元积分法: 设$x=\psi (t)$是单调的可导函数，并且${\psi }^{\prime }(t)\ne 0$. 又设$f[\psi (t)]{\psi }^{\prime }(t)$具有原函数，则有换元公式
$$\int f(x)dx={\left[\int f(\psi (t){\psi }^{\prime }(t)dt\right]}_{t={\psi }^{-1}(x)}$$
这种情况其实很难一眼直观看出来，三角函数相关的积分比较常见。
$$\begin{array}{rl}f(x)& =\sqrt{a^2-x^2}dx\\ & =a^2{\cos }^{2}t|dt(令x=a\sin t,-\frac{\pi }{2}<t<\frac{\pi }{2})\\ & =\frac{a^{2}t+\sin t\cos t}{2}+C\\ & =\frac{a^2\arcsin \frac{x}{a}+x\sqrt{a^2-x^2}}{2}+C(将t=\arcsin \frac{x}{a}带入)\end{array}$$
分部积分法：来源于两个函数乘积的导数计算公式。设函数$u=u(x),v=v(x)$具有连续导数，则$(uv{)}^{\prime }=u^{\prime }v+u{v}^{\prime }$，移项并求积分得到：
$$\int u{v}^{\prime }dx=uv-\int u^{\prime }vdx$$
也即$$\int udv=uv-\int vdu$$
$$\int x\cos xdx=x\sin x-\int \sin xdx=x\sin x+\cos x+C(其中u=x,v=\sin x)$$
通常来讲，希望取原函数的函数$u$的导数具有更简单的形式，从而$\int u^{\prime }vdx$具有更简单的形式。
积分示例
多项式积分
$$\begin{array}{rl}f(x)& =\frac{x}{x^2-x+1}\\ \int f(x)dx& =\int \frac{1}{2}\frac{2x-1}{x^2-x+1}+\frac{1}{2}\frac{1}{x^2-x+1}dx\\ & =\int \frac{1}{2}\frac{1}{x^2-x+1}d(x^2-x+1)+\int \frac{1}{2}\frac{1}{(x-\frac{1}{2}{)}^2+\frac{3}{4}}dx\\ & =\frac{1}{2}ln|x^2-x+1|+\frac{1}{\sqrt{3}}arctan\frac{2}{\sqrt{3}}(x-\frac{1}{2})+C\end{array}$$

万能公式
$$\begin{gathered} \begin{array}{rl}\int cscxdx& =\int \frac{1}{sinx}dx\\ & =\int \frac{1}{2sin\frac{x}{2}cos\frac{x}{2}}dx\\ & =\int \frac{si{n}^2\frac{x}{2}+co{s}^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}dx\\ & =\int \frac{ta{n}^2\frac{x}{2}+1}{2tan\frac{x}{2}}dx\end{array} \\ 令t=tan\frac{x}{2}，则x=2arctant， \\ \begin{array}{rl}\int cscxdx& =\int \frac{t^2+1}{2t}d(2arctant)\\ & =\int \frac{1}{t}dt\\ & =ln|t|+C\\ & =ln|tan\frac{x}{2}|+C\end{array} \end{gathered}$$
万能公式(三角函数转成$tan\frac{x}{2}$的多项式)也没那么万能，复杂多项式也不好求积分。
复数范围内积分
$$\begin{gathered} \int \frac{1}{1+x^2}dx=arctanx+C \\ 上式是通过arctanx的导数推导出来。然而根据多项式求积分方法 \\ \begin{array}{rl}\int \frac{1}{1+x^2}dx& =\int \frac{1}{(x+i)(x-i)}dx\\ & =\frac{i}{2}\int \frac{1}{x+i}-\frac{1}{x-i}dx\\ & =\frac{i}{2}ln\left(\frac{x+i}{x-i}\right)+C\end{array} \\ 两个结果相去甚远。但是其物理含义上，又是一致的。调整中间过程，可得 \\ \begin{array}{rl}\int \frac{1}{1+x^2}dx& =\int \frac{1}{(x+i)(x-i)}dx\\ & =\frac{1}{2}ln\left(\frac{1+xi}{1-xi}\right)+C\\ & =\frac{1}{2}ln\left(\frac{e^{\sqrt{1+x^2}arctanx}}{e^{-\sqrt{1+x^2}arctanx}}\right)+C\\ & =\frac{1}{2}\left(2arctanx\right)+C\end{array} \end{gathered}$$

定积分

众所周知，可以使用矩形(将圆弧使用平行于x轴横线来拟合)、梯形(将圆弧使用小块的连线来拟合)、辛普森法(将圆弧使用抛物线来拟合，估计在辛普森时代就已经知道了直线和抛物线围成图形面积的计算公式)求曲线和坐标轴围成的图形的面积，那么这么做是有误差的，难道误差就不管了吗？课本上并没有这个讨论，实际上，误差是更高阶无穷小，对误差进行一次积分的结果仍是无穷小，当$\Delta x\to 0$时，值为0.

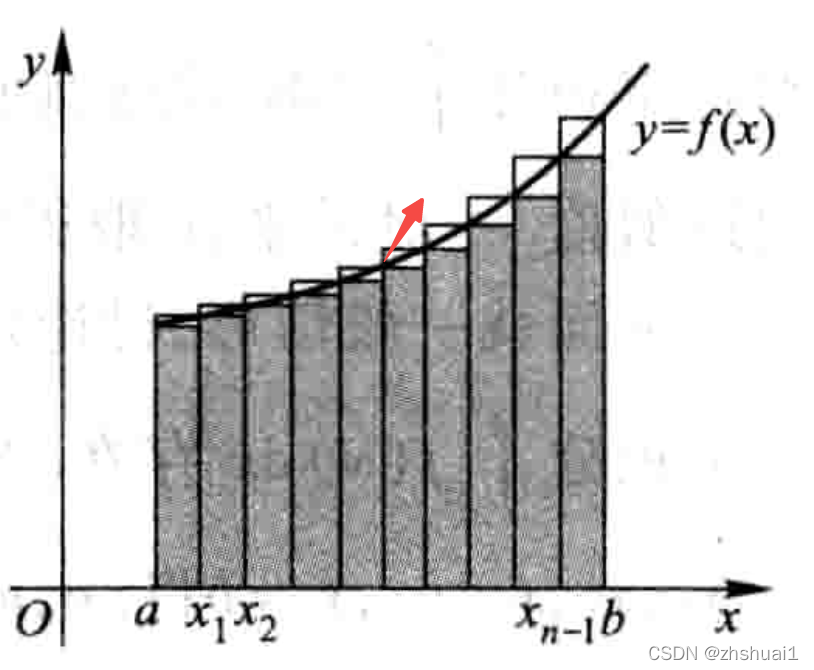
我们来说明一下这个问题，对于$x_i,x_{i+1}和f(x)$围成的图形面积$S_i$，其中矩形的面积为$S_{mi}$，曲线和矩形围成的面积为$S_{ri}$，有$S_i=S_{mi}+S_{ri}$. 假设$f(x)在[x_i,x_{i+1})$上，斜率的最大值和最小值分别是$k_{max}和k_{min}$，$S_{ri}$面积小于矩形和最大斜率直线围成的三角形面积，即$S_{ri}<(x_{i+1}-x_i)(x_{i+1}-x_i)k_{max}/2=k_{max}\Delta x^2/2$
$$\begin{array}{rl}S& =\underset{\Delta x_i\to 0}{\lim }\sum _{\Delta x_i\to 0}^n{S}_i=\sum _{\Delta x_i\to 0}^n(S_{mi}+S_{ri})\\ & =\underset{\Delta x_i\to 0}{\lim }\sum _{\Delta x_i\to 0}^n(f(x_i)\Delta x_i+k_{max}\Delta x^2/2)\\ & ={\int }_a^{b}f(x_i)dx+{\int }_a^b{k}_{max}/2d^{2}x\\ & ={\int }_a^{b}f(x_i)dx\end{array}$$
使用不同的方法求面积，进行同样小间隔的划分，能取得不同精度的原因是：它们的误差$S_{ri}$是$\Delta x_i$的不同阶数的无穷小，矩形、梯形、抛物线都是$\Delta x_i$的一阶无穷小，矩形误差是二阶，梯形误差是三阶，辛普森误差是四阶。如果存在一种划分，误差是$S_{mi}$对于$\Delta x_i$的同阶无穷小，则使用这种划分得到的面积和真实值相差一个常数。
含有瑕点的瑕积分不能直接通过原函数的积分上下限相减得到，必须根据瑕点分段求积分。
Q:$\Delta x\to 0时，弦长和弧长的差为什么是更高阶无穷小？$

微分方程

能使微分方程恒等的函数叫做微分方程的解；如果微分方程的解中含有任意常数，且任意常数的个数与微分方程的阶数相同，这样的解叫做微分方程的通解。

线性微分方程解的结构

对于二阶齐次线性微分方程：$y^{\prime \prime }+P(x)y^{\prime }+Q(x)y=0$
如果函数$y_1(x)$和$y_2(x)$是方程的两个解，那么$y=C_1{y}_1(x)+C_2{y}_2(x)$是方程的解，其中$C_1,C_2$为任意常数。如果$y_1(x)$和$y_2(x)$的两个线性无关的特解，那么$y=C_1{y}_1(x)+C_2{y}_2(x)$是方程的通解。
而对于二阶非齐次线性方程$y^{\prime \prime }+P(x)y^{\prime }+Q(x)y=f(x)$，如果$y^{\ast }$是他的一个特解，Y(x)是其对应的齐次方程的通解，则$y=Y(x)+y^{\ast }(x)$是二阶非齐次线性微分方程的通解。

常系数齐次线性微分方程

二阶常系数齐次线性微分方程通解：

特征方程的根和解的关系

常系数齐次线性微分方程特解的求法

对于f(x)的两种常见形式，有如下经验：
(1) $f(x)=e^{\lambda x}{P}_m(x)$，其中$\lambda$是常数，$P_m$是m阶多项式。
其特解形式为$y^{\ast }=x^k{R}_m(x)e^{\lambda x}$. $k$可以按照$\lambda$是方程的根的重数取$0,1,2,...$
(2) $f(x)=e^{\lambda x}(P_l(x)\cos \omega x+Q_n(x)\sin \omega x)$，其特解形式为$y^{\ast }=x^k{e}^{\lambda x}[R_m^{(1)}(x)\cos \omega x+R_m^{(2)}(x)\sin \omega x]$，k可按$\lambda +\omega i$是方程特征根的重数取$0,1,...$
以上两种情况可以使用欧拉公式合并下：
对于 $f(x)=e^{(\lambda +\omega i)x}{P}_m(x)$，其特解为$y^{\ast }=x^k{R}_m(x)e^{(\lambda +\omega i)x}$
因为常系数齐次线性微分方程的通解导致方程左边恒为0，实际上就是求y使得经过左侧方程运算之后能得到方程右边的函数。根据经验可以知道其特解应该有相对固定的形式，故可以使用待定系数法来确定系数。教材上为了通用给了一些例子，但是过于刻板了。
举个例子：$y^{\prime \prime }-2y^{\prime }-3y=3x+1$的特解，教材给的解法是带入通用公式，但其实大可不必，可以看做是：一个函数的二阶导数、一阶导数和本身的一个线性组合是$3x+1$，求这个函数。可以推出这个函数至多是个三阶多项式，设$y^{\ast }=a{x}^3+b{x}^2+cx+d$，求其一阶、二阶导数，带入微分方程，对比系数求得$a=0,b=0,c=-1,d=1/3$

计算机解法

sympy是个符号计算库，在诸多方面不完善，但是对于日常的辅助计算，已经非常足够了。

import sympy as sp
sp.init_session() # 导入sp相关基本变量 x, y, z; i, j, k(Integer); f, g(Function)
f.assumptions0 # 展示f的假设; Function
sinc(pi/6).evalf(6) # 求出数值解，保留6位有效数字
p = Piecewise((0,x<-1),(x**2,x<=1),(0,True)) # 分段函数
ff = 1/(x**4+1) 
int_ff = Integral(ff, x)
int_ff.doit()
# 上述等价于 integrate(ff, x)
ff.subs(x**2, t) # 换元
ff = x + y + 4 
ff.subs({x:3,y:t,4:1}) # 替换，部分求和
ff = sp.exp(x**y)
ff.diff(x,x,y) # 对x求2次偏导，再对y求1次偏导
ff.diff(x,2,y,3) # 对x求2次偏导，再对y求3次偏导
ff.apart() #部分分式展开
ff.expand() # 因式展开
ff.factor() # 因式分解
ff.series(x, 10) # 泰勒展开(洛朗展开)
ff.series(x,y,10) # 二阶泰勒展开
ff.simplify() # 启发式化简
diffeq = [sympy.Eq(f(x).diff(x, x) - f(x), sympy.sin(x)), sympy.Eq(g(x).diff(x), 0)]
res = sympy.dsolve(diffeq, [f(x), g(x)], ics={f(0): 1, f(x).diff(x).subs(x, 0): 3}) # 指定初值，求解微分方程