深度学习第二章 概念补充

这一节就之前涉及到的一些概念做一个整理，大部分是来自百度，出处急切之前搞不清楚了，下面内容是个人整理的，如果感觉有一点前言不搭后语，可直接复制粘贴相关内容，进行百度。我只是搬运工。

可以放轻松，如果有些概念忘记了，不要纠结，先放过。等到有具体的应用场景时，再回来进行参考佐证。

导数

定义：设函数y=f(x)在点x0的某个邻域内有定义，当自变量x在x0处有增量Δx，(x0+Δx)也在该邻域内时，相应地函数取得增量Δy=f(x0+Δx)-f(x0)；如果当Δx→0时， Δy与Δx之比极限存在，则称函数y=f(x)在点x0处可导，并称这个极限为函数y=f(x)在点x0处的导数，记作：

下面以一元二次函数作为例子：

A是曲线方程 y = f(x)上的点，l是经过A的切线， ∠HAB的正切值代表了切线的斜率， △x -> 0的过程中，点C不断逼向点H，最终两者重合。

 

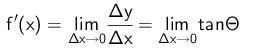
简单起见，令 θ = ∠HAB，当 △x 取极限时，曲线上某点的导数 = 过该点切线的斜率。需要澄清的一个概念是： 虽然导数有正有负，它仍然是一个标量 

方向导数

从一元扩展到多元方程时，情况就变得有点复杂了。首先，多元函数代表的函数图像不再是一条曲线，而是一个曲面（超曲面），通过曲面上的某一点，可以作无数条切线（这里我只讨论可导的情况），这就引出了方向导数的概念，还是先看数学定义：

定义：设函数 z = f(x, y)在点 p(x, y) 的某一邻域 U(p) 内有定义，自点 p 引射线 l， 设 x 轴到射线的转角位 φ， 并设 p'(x + △x, y + △y) 为 l 上的另一点且 p' ∈U(p)，我们考虑函数的增量 f(x + △x, y + △y) - f(x, y) 与 p、p'两点距离 ρ = sqrt( (△x)² + (△y)² )的比值， 当 p' 沿 l 趋向 p 时， 如果这个比的极限存在，则成这个极限为函数 f(x, y) 在点 p 沿方向 l 的方向导数，即：

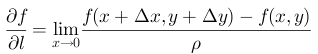
这个定义是我从其他的地方抄的，看不懂 ？ 没关系，现在我们分步讲解。

 

上图展示了如何求一个二元函数的方向导数，整个过程可分两步来理解：

方向性

方向导数，顾名思意，是某个方向上的导数，需要从方向性与导数性两方面来考虑。方向性比较容易理解：点A（不一定是原点）是 f(x, y) 上的点， 从点A出发，做一条射线 l， 射线 l 指向的方向就是我们需要研究的对象， 很明显，射线 l 平行于 xoy平面 或 l 在 xoy平面上。

导数性

沿射线 l 作 一个垂直于 xoy 的平面，该平面与二元函数的图像相交，形成一条空间上的曲线（图中标黄色的部分），如果这条曲线以射线 l 的方向作为横轴，Z方向作为纵轴，则可以理解为一个以 Z-A-L 为坐标系的一元函数曲线，利用一元函数的性质，可以很容易求出该曲线在 A 点的导数，为了表达清晰，我将A、B、C三点平移到 A'、B'、C'，∠B'A'C'的正切值就是A点的导数值，这个导数就是我们所说的方向导数。

需要注意的是，方向导数虽然有方向这个帽子，但它任然是标量。

偏导数

 如果选定方向平行于X轴，则改该方向导数称为 f(x,y) 对 x 的偏导数，如果选定方向平行于Y轴，则改方向导数称为 f(x,y) 对 y 的偏导数，记为：

 

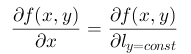
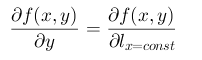
偏导数是方向导数的特殊情况。

全导数

前面讨论的方向导数、偏导数都是多元函数里面的概念，全导数则是复合函数里面的概念，这是需要我们仔细区分的，例如：

设u=u(x)、v=v(x)在x可导，z = f(u,v) 在相应点 (u,v) 有连续偏导数，则复合函数 z=f(u(x), v(x)) 在x可导，且有：　

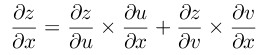
称 ∂z/∂x 为函数 z = f(u, v) 相对变量 x 的全导数， 而 z 相对于自变量 u、v来说是二元函数， 不存在全导数之说。 

全微分

定义： 如果函数 z = f(x, y) 在定义域 D 内的点 (x, y) 处的全增量 △z = f(x + △x, y + △y)， 可表示成

 

 

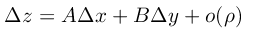
其中

 

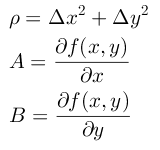
其中，A、B不依赖于 △x， △y，仅与 x， y 有关，o(ρ)是关于ρ的高阶无穷小， 则称 f(x,  y)在点 (x,  y)处可微，A△x + B△y 称为函数 f(x,  y)在点 (x,  y)的全微分，记做：

 

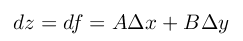
在讲解全微分之前，需要对导数与微分他们微妙的差别做一下区分！

我们在讨论导数时，总是会先确定一个自变量和一个因变量，然后把变化量取极限时的比例定义为导数（比如方向向量中的 ∂f 与 ∂l），对应的物理意义就是切线的斜率

微分研究的对象则是：在函数的某个邻域D内，当变化量取极限时，因变量的变化 (△z) 是否可以用一个自变量的变化（△x，△y）的线性方程来表示，注意这个邻域是一个空间的概念，

这是区分可导与可微的关键。

可导 --> 可微 (不成立)

可微 --> 可导 (成立)

上面是一幅微分逼近的示意图，前面我们在讨论方向导数时，明确规定 △x， △y 是沿着直线 l 对函数 f 进行逼近，而全微分研究的范围是某个邻域D，也就是说 l 是一条曲线，△x， △y沿着任意曲线对函数 f 进行逼近也是可以的，可以看到可微对函数的质量（光滑度）要求高的多（可导只能保证线性方向是线性光滑的，可微表示邻域内的任意位置都是线性性光滑的）。

方向导数与偏导数

给定一个二元函数，我们如何求其方向导数。从定义上将，我们需要作出这条代表方向的射线，看其在函数上的投影曲线，作出投影曲线的切线，再量出切线与 xoy平面的夹角，求其正切值得到方向导数，但实际应用中，我们几乎没法作出投影曲线，更不可能量出切线的夹角，如何求方向导数？

高等数学给了我们一个简便的工具用来计算方向导数，但是使用这个工具前对我们的函数有一个小小的要求，那就是要求函数在该点可微（幸好我们实际应用中的大部分问题都满足这一条件）！

根据全微分的定义有：

两边同时除以 ρ：

 

左边就是方向导数的定义

再来看右边，因为 o(ρ) 是 ρ 的高阶无穷小，在做除法时可以忽略不计，根据勾股定理（看前面关于全微分的定义）△x、△y，ρ是构成了直角三角形的三条边，令:

 化简之后就可变成了我们方向导数的计算表达式：

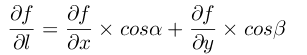
这里之所以都使用余弦表示是为了方便向更高维扩展，而且向高维扩展时，满足关系式：

 

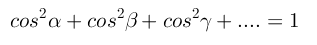
梯度

https://www.cnblogs.com/bingjianing/p/9014246.html

 定义： 设函数 z = f(x, y) 在平面区域D可微分（不少参考资料将这里描述为具有一阶连续偏导数，个人认为此条件过于宽泛，实际上后面的推导都是基于全微分的前提下进行的），则对于每一点(x, y) ∈ D，都可定出一个向量：

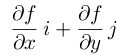
称这个向量为函数 z = f(x, y)的梯度， 记作：

 

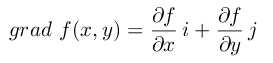
上面以二元函数为例进行定义，扩展到高维大家自行想象。

注意，梯度是不同于我们前面所述的任何一个概念，它是一个矢量，即有大小，又有方向。

梯度向量处于 xoy 平面， 向量[∂f/∂x, ∂f/∂y] 决定了了梯度的方向，可以把梯度的角色理解成前面所说的直线 l （方向导数中代表方向的射线），实际上它就是一个特殊的 l：

沿着梯度方向的方向导数最大，并且方向导数最大值为梯度的长度。

这是一条很重要的性质，下面就来对其证明：

根据方向导数的计算表达式（以可微为前提）：

u是梯度向量，v是方向 l 所代表的单位向量，||v||的结果为1， 函数 f 与点 P 确定之后，||u||的值也唯一确定，现在只能通过改变 u 和 θ 来该表方向导数的大小

从定义式可以看出， θ  = 0 时，方向导数达到最大，最大的方向导数：

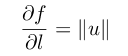
梯度官方定义

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）