概率论重难点例题

一、随机变量函数的分布（Chap 2.5）

类型一：X为离散型变量，则Y也为离散型变量

例题

【注】同一个x，可能y相同

类型二：X为连续型——分布函数法

方法：

【注】

1. 用概率P（即分布函数 F）将X和Y联系在一起，求出F_Y(y)，再求f_Y(y)）
2. 可见0和1球求导之后都是0，所以不能由f_Y(y)=0得出F_Y(y)=0

例1 X与Y为线性关系

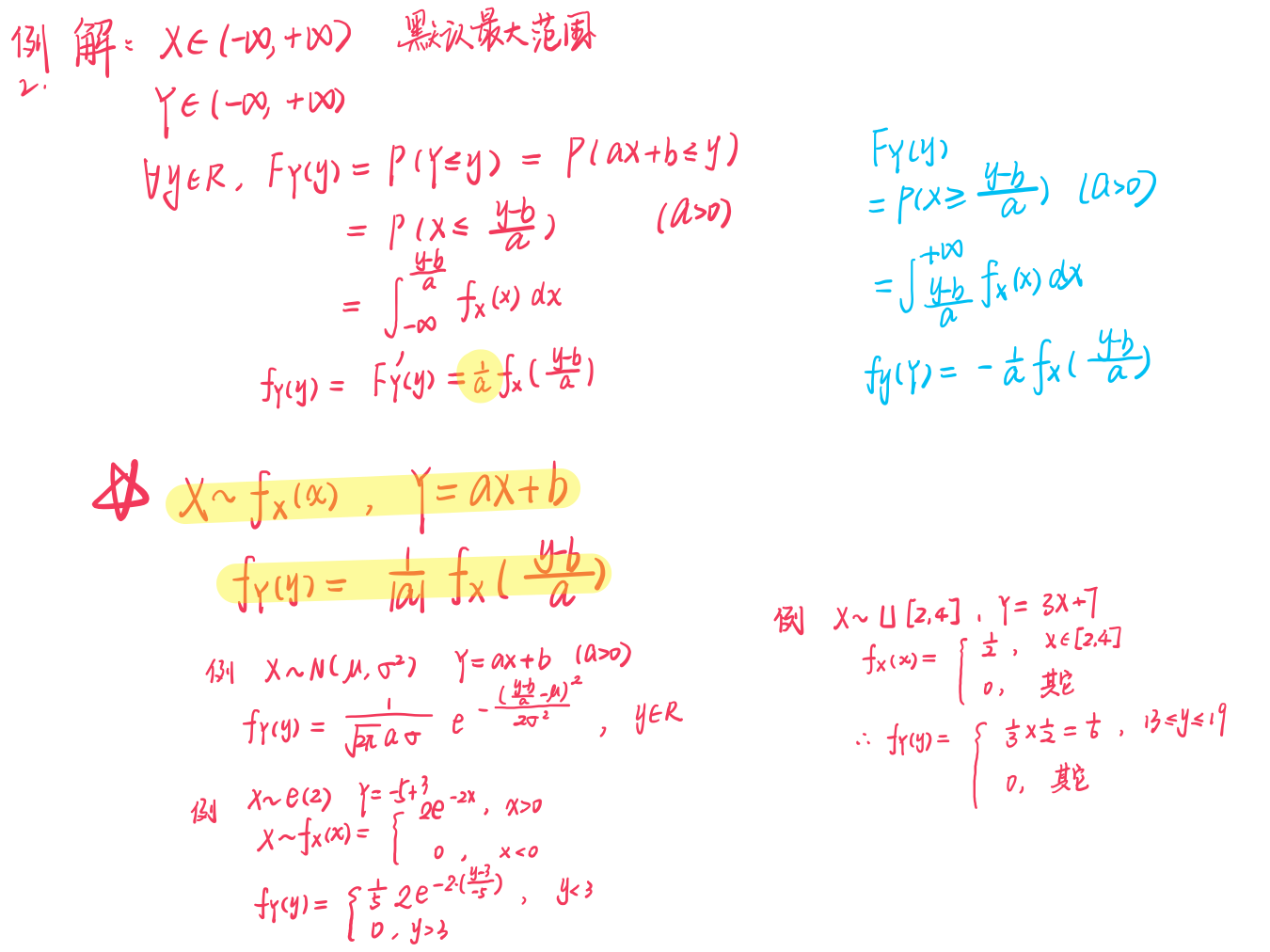
【总结】

1. 记住结论，注意y的范围与x的范围对应
2. 分情况：a>0和a<0（a的正负会影响不等式的符号，从而因影响积分F_Y(y)
3. 会变上限积分，注意有复合函数的积分 Why?

例2 X与Y为幂函数关系

【总结】

1. 记住结论（稍微有点难记，也可以自己推导）
2. 分情况：n为奇数还是偶数，y的范围(-∞，+∞）还是（0，+∞)
3. 一定要作图辅助解不等式
4. 会变上限积分，注意有复合函数的积分

例3 X(正态分布)与Y=X² (例2的特例)

【伽马函数】
见概率论w(1)1.pdf P128
【初步了解】
正态分布、卡方分布、伽马分布的关系

例4 由指数分布生成均匀分布

【结论】

1. 指数分布（本题）、伽马分布、正态分布都可以通过Y去其本身的分布函数，从而转化为均匀分布
2. 同样，均匀分布也可以转化为其他分布（见例5）
3. 均匀分布是最特殊的分布

例5 由均匀分布生成指数分布

【注意】

1. 对数函数要有意义，x不能取1
2. 注意X和Y的关系（同例4进行比较）

例6 X和Y为三角函数关系

二、条件分布（Chap 3.3）

类型一、二维离散型随机变量

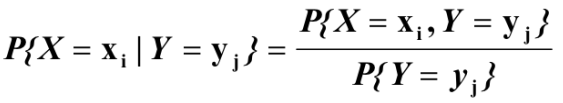因为

【注】

1. 条件分布是分布律，且是一维分布， 因为有一个变量固定了，只有一个变量
2. 求条件分布律，首先要求联合分布律和边缘分布律

例一

例二 射击问题

【注】

1. 求联合分布律的时候，i和j是固定的，所以概率不需要考虑位置问题
2. 边缘分布分别是几何分布和负二项分布，符合实际意义
3. 首次中的前提下，第二次中又是一个新的几何分布；在第二次中的前提下，第一种中是可能的，均符合实际意义

类型二、二维连续型随机变量

特别注意！
因为连续性变量在一点的概率为0 ，所以分母上一定不能出现P(Y=y)，只能用概率密度函数f来代替概率P,同样，条件密度=联合密度÷边缘密度

例一

【注】

1. 联合密度转化为边缘密度的方法：将另一个变量从-∞到+∞积分
2. 由条件概率密度到条件分布函数，即积分的过程，特别注意，趋向于-∞的时候，条件分布函数=0，趋向于+∞的时候，条件分布函数=1，中间段积分积出来，会有一个常数C，用连续型求出C
3. 再求第三小问的时候，既可以再积分，也可以直接用求得的条件分布函数代值计算，二者结合可以检查
4. 结论：均匀分布的而条件分布还是均匀分布（可以用作检查手段）

例二

【注意】
注意变式3，条件不再是一个值，而是一个范围，此时，用原始的定义，分母不再为0

三、随机向量函数的分布（Chap 3.6）