最短路径问题

最短路径

最短路径是指在一个图（Graph）中，从一个顶点（Vertex）到另一个顶点之间经过的边的权重和最小 的路径。

这里的“权重”通常指的是边的某种度量值，比如距离、时间、成本等，但在最短路径问题中， 通常假设这些权重都是非负的。

最短路径问题是图论中的一个基本问题，它要求找到图中两个顶点之间的最短路径。这个问题在多个领 域都有广泛的应用，比如网络路由、城市规划、地理信息系统（GIS）、社交网络分析等。

迪杰斯特拉算法

• 需要指定一个起点D(即从顶点D开始计算)。

• 引进两个数组S和U。（互补）

  • S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，
  • U 则是记录还未求出最短路径的顶点(以及该顶点到起点D的距离)

• 初始时，数组S中只有起点D；(自己到自己认为是0)；

示例

选取顶点（计算邻接点最短路径，非邻接点举例用∞表示）

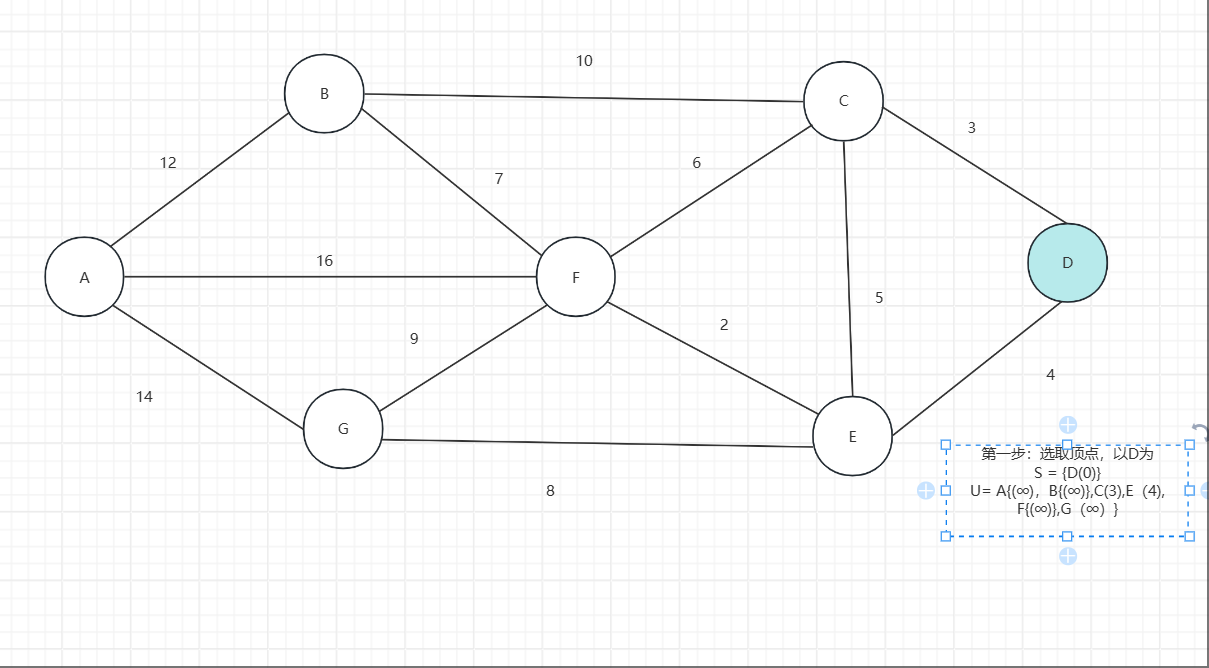
选取U中最短距离顶点，作为下一个顶点，同时将该顶点从U中出列，在S中入列，同时更新U中路 径信息

选取顶点E

选取顶点F

选取顶点G

选取顶点B

F%E5%BE%84%5C7.png&pos_id=img-QsfehnZB-1747289507913)

选取顶点A

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

#include <iostream>
using namespace std;
#include <vector>
// 定义边
typedef struct Node
{
    int weight; /// 边的权重
    int vertex; // 下一个顶点（邻接点）的值
    struct Node *next;
     // 下一条顶点（如果当前顶点没有更多的邻接点，则此指针为NULL）
} Node;

// 定义图
typedef struct Graph
{
    int numVertices; // 顶点数
    Node **adjList;  // 邻接表
    bool *isVisited;
} Graph;

// 创建图并且初始化
Graph *createGraph(int vertis)
{
    // 给图申请内存
    Graph *grash = new Graph();
    if (!grash)
    {
        perror("申请失败");
        return 0;
    }
    // 初始化顶点数
    grash->numVertices = vertis;
    // 邻接表申请内存
    grash->adjList = new Node *[vertis];
    if (!grash->adjList)
    {
        perror("申请失败");
        return 0;
    }
    // 邻接表初始化
    for (int i = 0; i < vertis; ++i)
    {
        // adjList 是一个二级指针数组，即它是一个指针的数组，每个指针都指向一个链表
        // adjList[i] 是对指针数组的第 i 个元素进行解引用，得到的是一个一级指针
        //  grash->adjList[i] 设置为 nullptr，意味着对于图中的每个顶点 i，其对应的邻接链表的起始指针被初始化为空，表示在初始化时，每个顶点都没有任何邻接的边或者节点。
        grash->adjList[i] = nullptr;
    }
    // 标记位申请内存
    grash->isVisited = new bool[vertis]{0};

    return grash;
}
// 添加边 src起点 dest终点
void addEdge(Graph *graph, int src, int dest, int weight)
{
    // 为源顶点创建一个新节点
    Node *newNode1 = new Node;
    if (!newNode1)
    {
        perror("申请失败");
        return;
    }
    // 设置邻接点
    newNode1->vertex = dest;
    // 设置权重
    newNode1->weight = weight;
    // 将新边添加到起点的链表中 头插
    newNode1->next = graph->adjList[src]; //新节点的 next 指针指向当前 src 邻接链表的第一个节点。
    // 这样，新节点 newNode1 被插入到链表的头部
    graph->adjList[src] = newNode1; // 将 src 的邻接链表的头部更新为 newNode1。
    // 这样，newNode1 成为链表的新头节点
    // 如果是无向图，也需要添加反向边
    Node *newNode2 = new Node;
    if (!newNode2)
    {
        perror("申请失败");
        return;
    }
    // 设置邻接点
    newNode2->vertex = src;
    // 设置权重
    newNode2->weight = weight;
    // 将新边添加到起点的链表中 头插
    newNode2->next = graph->adjList[dest]; // 将新节点的 next 指针指向当前 src 邻接链表的第一个节点
                                           // 更新第一条边
    graph->adjList[dest] = newNode2; // 将 src 的邻接链表的头部更新为 newNode。这样，newNode 就成为 src 的邻接链表的第一个节点
                                     // 如果是无向图，也需要添加反向边
}

// 迪杰斯特拉算法
void dijkstra(Graph *graph, int src) // src 是当前顶点
{
     //距离：定义一个包含numVertices个元素的vector，每个成员用INT_MAX（∞）初始化
     vector<int> dist(graph->numVertices, INT_MAX);//U数组 存储最短距离
     //标记顶点是否被处理过了
     vector<bool>sptSet(graph->numVertices, false);
    //  自己到自己的距离是0
    dist[src] = 0;
    //-1的原因是最后一部实际上已经没必要再执行了，即A的遍历，因为最短距离已经计算出来了
    for(int count = 0;count < graph->numVertices; ++count)
    {
        // 存储最小距离，方便比较
        int minDistance = INT_MAX; 
        // 最小距离的顶点坐标信息，并标记为已处理
        int minVertices = -1;
        //遍历所有顶点(第一步选中的必定是自身，因为自身的距离是0，肯定最小)
        // 找到U里面最短距离及其下标
        for(int i = 0; i < graph->numVertices; i++)
        {
             //顶点未被处理过并且距离小于最小值
            if(!sptSet[i] && dist[i] < minDistance)
            {
                // 更新最小距离
                minDistance =  dist[i] ;
                 //记录顶点
                minVertices = i ;
            }
        }
        //该顶点标记为已处理
        sptSet[minVertices] = true;
        // 更新该顶点的所有邻接点（未被标记过的）的最短距离 
        // 顶点 minVertices 的邻接链表的第一个节点
        Node *current = graph->adjList[minVertices];
        while(current)
        {
            //邻接点的值
            int adj = current->vertex;
            // /邻接点未被标记过 && 最小距离不是无穷（即是一个有效的距离，意味着他到源顶点是可
// 达的）&& 新距离小于原来的距离
            if(!sptSet[adj] && dist[minVertices] != INT_MAX && dist[minVertices] + current->weight < dist[adj])
            {
                 //更新距离信息 新的两边相加距离加入到    dist[adj]里面就是当前最短路径
                 dist[adj] = dist[minVertices] + current->weight ;
            }
            current = current->next;
        }
    }
      // 打印构造的距离数组  
      for(int i = 0; i <  graph->numVertices; i++)
      {
            cout <<  "Vertex " << i  <<  " Distance from Source: " <<  dist[i] << endl;
      }
   
}

 // 清理Graph对象  
 void freeGraph(Graph* graph)
 {
    if (!graph)
    {
        return; // 如果指针为空，则直接返回  
    }
    // 释放邻接表中每个链表占用的内存  
    for(int i = 0; i < graph->numVertices; i++)
    {
         Node *current = graph->adjList[i]; 
         Node *newDeNode = nullptr;
         while(current)
         {
            newDeNode = current;
            delete newDeNode;
            current = current->next;
         }
    }
    // 释放邻接表数组本身占用的内存
    delete[] graph->adjList;
    // 释放访问标记数组占用的内存 
    delete[] graph->isVisited;
 }

int main()
{
    Graph* graph = createGraph(7);
    addEdge(graph, 0, 1, 12);
    addEdge(graph, 0, 5, 16);
    addEdge(graph, 0, 6, 14);

    addEdge(graph, 1, 2, 10);
    addEdge(graph, 1, 5, 7);

    addEdge(graph, 2, 3, 3);
    addEdge(graph, 2, 4, 5);
    addEdge(graph, 2, 5, 5);
    
    addEdge(graph, 3, 4, 4);

    addEdge(graph, 4, 5, 2);
    addEdge(graph, 4, 6, 8);

    addEdge(graph, 5, 6, 9);

    dijkstra(graph, 3);

    delete(graph);
    graph = nullptr;
   return 0;
}

结果是

广度优先遍历（从顶点2开始）:
Visited 2
Visited 0
Visited 3
Visited 1

• 问题一：只定义一个S，不定义U可以吗

可以，S和U是互补的，定义一个就行

• 问题二 sptSet[adj]写成sptSet[minVertices]

不一样 sptSet[minVertices]是当前源节点最小的顶点， sptSet[adj】其实就是邻接点 条件其实要判断邻接点未被标记过

或者说minVertex 是当前找到的最近的未处理顶点，而 adj 是 minVertex 的邻接点

• graph->adjList[minVertex] 是一个链表，存储了 minVertex 的所有邻接点的信息。
• 在更新距离时，通过遍历 graph->adjList[minVertex]，找到 minVertex 的所有邻接点，并更新这些邻接点的距离