搞懂CRF

1 前言

条件随机场(conditional random field, CRF)是在建立序列模型时的常用模块，它的本质就是描述观测到的序列$\bar{x}$对应的状态序列$\bar{y}$的概率，记作$P(\bar{y}|\bar{x})$。这里字符上的横线表示这是一个序列，下文中所有的序列都会带这个横线，不带横线就不是序列。

它是HMM的升级版，如果不熟悉HMM的话，建议看我的搞懂HMM这篇文章，不看那篇，直接看这篇关系也不大。

提出CRF是为了改进MEMM(maximum-entropy Markov model)的label bias问题，而提出MEMM是为了打破HMM的观测独立性假设。这些在下文中会进一步说明。

本文主要是参考了Log-Linear Models, MEMMs, and CRFs，其中会额外补充一些东西，并加入自己的一些理解。

2 Log-linear model

CRF的源头就是Log-linear model，是由它一点点改进过来的。

我们先假设观测变量为$x$，观测集合为$X$，有$x\in X$，比如$x$是一个单词；状态变量为$y$，状态集合为$Y$，有$y\in Y$，比如$y$是某种词性；提取特征的函数向量为$\bar{\varphi }(x,y)$，这里带了横线，表示有多个函数；函数之间的权重为$\bar{w}$。那么在给定$x$的情况下，$y$的概率为（比如单词$x$是词性$y$的概率）

$$p(y|x;\bar{w})=\frac{exp(\bar{w}\cdot \bar{\varphi }(x,y))}{{\sum }_{y^{\prime }\in Y}exp(\bar{w}\cdot \bar{\varphi }(x,y^{\prime }))}\text{\hspace{1em}(2-1)}$$

式$(2-1)$的分子表示给定$x$时，$y$取某个值时的指数计算式；分母表示表示给定$x$时，$y$取所有情况的指数计算式之和。说白了就是一个归一化的操作。

使用指数$exp$是为了保证概率都是正的，$\bar{w}\cdot \bar{\varphi }(x,y)$可正可负。

显而易见，在这种定义下可以保证

$$\sum _{y\in Y}p(y|x;\bar{w})=1\text{\hspace{1em}(2-2)}$$

假设我们有$n$组有标签的数据 { ( x i , y i ) } i = 1 n \{(x_i, y_i)\}_{i=1}^{n} {(xi​,yi​)}i=1n​，这里还没有涉及到序列，可以理解为一个单词$x_i$对应一个词性$y_i$的数据集。

我们的目的是调整模型的参数$\bar{w}$，使得出现数据集这样的标签对应情况的可能性最大，也就是

$${\bar{w}}^{\ast }=arg\underset{\bar{w}}{\max }\prod _{i=1}^{n}p(y_i|x_i;\bar{w})\text{\hspace{1em}(2-3)}$$

为了方便计算，通常会取对数，即

$${\bar{w}}^{\ast }=arg\underset{\bar{w}}{\max }\sum _{i=1}^{n}log(p(y_i|x_i;\bar{w}))\text{\hspace{1em}(2-4)}$$

通常为了不让模型学偏，把$\bar{w}$学的特别大来糊弄过去，还会加一个正则项

$${\bar{w}}^{\ast }=arg\underset{\bar{w}}{\max }\sum _{i=1}^{n}log(p(y_i|x_i;\bar{w}))-\frac{\lambda }{2}||\bar{w}|{|}^2\text{\hspace{1em}(2-5)}$$

这也就是损失函数，有了损失函数之后就可以用梯度下降的方法求参数${\bar{w}}^{\ast }$了。

这只是针对于非序列的数据集。

3 MEMM

3.1 模型概述

MEMM(maximum-entropy Markov model)进一步将问题从$p(y|x)$转变为$p(\bar{y}|\bar{x})$，也可以写成

$$p(y^1,y^2,...,y^m|x^1,x^2,...,x^m)\text{\hspace{1em}(3-1)}$$

其中，$x^j$表示序列中的第$j$个token，比如一句话中的第$j$个单词；$y^j$表示序列中的第$j$个标签，比如一句话中的第$j$个单词的词性；$m$表示序列的长度。

用$Y$表示所有可能的标签集合，这是一个有限的集合，$y^j\in Y$。

将式$(3-1)$用条件概率进行变换就有

$$p(y^1,y^2,...,y^m|x^1,x^2,...,x^m)=\prod _{j=1}^{m}p(y^j|y^1,...,y^{j-1},x^1,...,x^m)\text{\hspace{1em}(3-2)}$$

式$(3-2)$仅仅是一堆条件概率，这是必然成立的，没有任何假设。我们如果把HMM中的齐次马尔可夫假设放到这里来，认为$y^j$只受$y^{j-1}$的影响，那么就有

$$p(y^1,y^2,...,y^m|x^1,x^2,...,x^m)=\prod _{j=1}^{m}p(y^j|y^{j-1},x^1,...,x^m)\text{\hspace{1em}(3-3)}$$

这里仍旧认为$y^j$受所有$x^j$的影响，这就打破了HMM中的观测独立假设。这是一个在很多任务中不合理的假设，所以MEMM算是对HMM做了改进。画成概率图就是

图3-1 MEMM概率图

有很多的CRF的文章都是从概率图开始讲的，但其实根本没有必要，不是先有了图3-1才有了式$(3-3)$，而是先有了式$(3-3)$才有了图3-1，图3-1仅仅只是让式$(3-1)$看起来更方便了。不知道概率图，一点关系都没有。

不过既然画了概率图，也顺嘴说一句，MEMM的概率图和HMM的概率图的区别就在于$x$的箭头方向反了，从生成模型变成了判别式模型；以及MEMM是所有的$x$指向每一个$y^j$，而HMM是$x^j$指向$y^j$，打破了观测独立假设。

好，回到式$(3-3)$，利用log-linear model进行建模，就有
$$p(y^j|y^{j-1},x_1,...,x_m)=\frac{exp(\bar{w}\cdot \bar{\varphi }(x^1,...,x^m,j,y^{j-1},y^j))}{{\sum }_{y^{\prime }\in Y}exp(\bar{w}\cdot \bar{\varphi }(x^1,...,x^m,j,y^{j-1},y^{\prime }))}\text{\hspace{1em}(3-4)}$$

注意对比一下式$(3-4)$和式$(2-1)$的区别，就是条件概率中的条件变了。

将式$(3-4)$代入式$(3-3)$就有

$$\begin{gathered} p(y^1,y^2,...,y^m|x^1,x^2,...,x^m)= \\ \prod _{j=1}^m\frac{exp(\bar{w}\cdot \bar{\varphi }(x^1,...,x^m,j,y^{j-1},y^j))}{{\sum }_{y^{\prime }\in Y}exp(\bar{w}\cdot \bar{\varphi }(x^1,...,x^m,j,y^{j-1},y^{\prime }))}\text{\hspace{1em}(3-5)} \end{gathered}$$

这里在训练模型的时候，不是拿式$(3-5)$这个大家伙去训练的，而是训练$p(y^j|y^{j-1},x_1,...,x_m)$这个模型。

有了$p(y^j|y^{j-1},x_1,...,x_m)$之后，任何的$x$和$y^{j-1}$，$y^j$进来都可以输出一个概率值，问题就变成了如何decoding，如何推理，即求

$$arg\underset{y^1,..,y^m}{\max }p(y_1,..,y^m|x^1,...,x^m)\text{\hspace{1em}(3-6)}$$

如果我们假设$Y$集合中有$k$个元素的话，那么$y^1,...,y^m$就有$k^m$种组合，这样的计算量就太大了。这个时候，就要用动态规划了，这里的动态规划有一个自己的名字，叫做viterbi算法，其实就是动态规划。

我们会建立一个矩阵$\pi [j,y]$，$j=1,...,m$并且$y\in Y$。$\pi [j,y]$存储了在第$j$个位置，状态取$y$时的最大概率值和得到该概率值的序列$y^1,..,y^j$。可以表示为

$$\pi [j,y]=\underset{y^1,...,y^{j-1}}{\max }(p(y|y^{j-1},x^1,...,x^m)\prod _{k=1}^{j-1}p(y^k|y^{k-1},x^1,...,x^m))\text{\hspace{1em}(3-7)}$$

其中，最开始的为初始变量，相当于HMM中的初始概率

$$\pi [1,y]=p(y|y^0,x^1,...,x^m)\text{\hspace{1em}(3-8)}$$

$y^0$就是"<START>"这样的起始token。

之后是通过迭代得到的

$$\pi [j,y]=\underset{y^{\prime }\in Y}{\max }(\pi [j-1,y^{\prime }]\cdot p(y|y^{\prime },x^1,...,x^m))\text{\hspace{1em}(3-9)}$$

将$\pi [j,y]$这个矩阵填满之后，就有

$$\underset{y^1,...,y^m}{\max }p(y^1,...,y^m|x^1,...,x^m)=\underset{y}{\max }\pi [m,y]\text{\hspace{1em}(3-10)}$$

MEMM相比于HMM的优势在于

• 观测变量不再独立
• 可以自行设计$\bar{\varphi }$，对结果更可控

3.2 label bias问题

MEMM也存在自身的问题，这个问题被称为label bias问题，故名思义，这是由于训练数据标签的不平衡所导致的，如果训练数据足够大，标签足够平衡，就没有这个问题。出现这个问题的根本原因就是$p(y^j|y^{j-1},x^1,...,x^m)$是在每个时间节点都做了一次归一化，丢失了一些信息。

下面举个例子来试着说明一下，只要有一个直观的理解就可以了，不要太纠结例子的合理性。

假设我们通过训练得到了下图3-2这样的一张概率值推理图，我们输入[“the”, “cat”, “sat”]，可以发现[“ARTICLE”, “NOUN”, “VERB”]这样的概率是最高的，有$1.0\ast 0.9\ast 1.0=0.9$。

图3-2 概率值推理图

但是，当我们的输入是[“cat”, “sat”]的时候，就会发现[“NOUN”, “VERB”]的概率只有$0.1\ast 1.0=0.1$，而[“ARTICLE”, “NOUN”]的概率有$0.9\ast 0.3=0.27$。这是因为以"cat"为开头的句子，模型见的很少。如果可以在计算当中把模型见的很少这个信息也带上的，就可以避免这个问题了。

下面来看下图3-2对应的逻辑图，如下图3-3所示，就是没有归一化的图。

图3-3 逻辑值推理图

归一化是$e^x$这样的指数归一化，可以动手算下看，是和图3-2的概率值对应上的。这里[“cat”, “sat”]这个例子的[“NOUN”, “VERB”]就是$3+100=103$，而[“ARTICLE”, “NOUN”]就变成了$5+21=26$。用加法是因为这里都是log值。

这里就说这么多，只是给个直观的理解，想要细究的，可以看下The Label Bias Problem，或是自行搜一下其他大佬是怎么说的。

4 CRF

4.1 模型概述

有了前面那么多的铺垫，CRF(conditional random filed)就很容易理解了。MEMM是对式$(3-4)$进行建模，而CRF是对式$(4-1)$进行建模

$$p(y^1,...,y^m|x^1,...,x^m)=p(\bar{y}|\bar{x})\text{\hspace{1em}(4-1)}$$

注意式$(2-1)$，式$(3-4)$和式$(4-1)$的区别。CRF没有局部的归一化了，只有全局的归一化，说白了就是一个考虑序列的log-linear模型。

$$p(\bar{y}|\bar{x};\bar{w})=\frac{exp(\bar{w}\cdot \bar{\Phi }(\bar{x},\bar{y}))}{{\sum }_{{\bar{y}}^{\prime }\in Y^m}exp(\bar{w}\cdot \bar{\Phi }(\bar{x},{\bar{y}}^{\prime }))}\text{\hspace{1em}(4-2)}$$

其中，$Y^m$表示用$Y$中的元素组成长度为$m$的序列的所有可能的序列集合。

这里还把$\bar{\varphi }$变成了$\bar{\Phi }$，$\bar{\Phi }$的定义为

$$\bar{\Phi }(\bar{x},\bar{y})=\sum _{j=1}^m\bar{\varphi }(\bar{x},j,y^{j-1},y^j)\text{\hspace{1em}(4-3)}$$

这里的$\bar{\varphi }(\bar{x},j,y_{j-1},y^j)$和MEMM中的是一模一样的，都是人为定义的特征函数。只不过是把整个序列的都加到了一起。

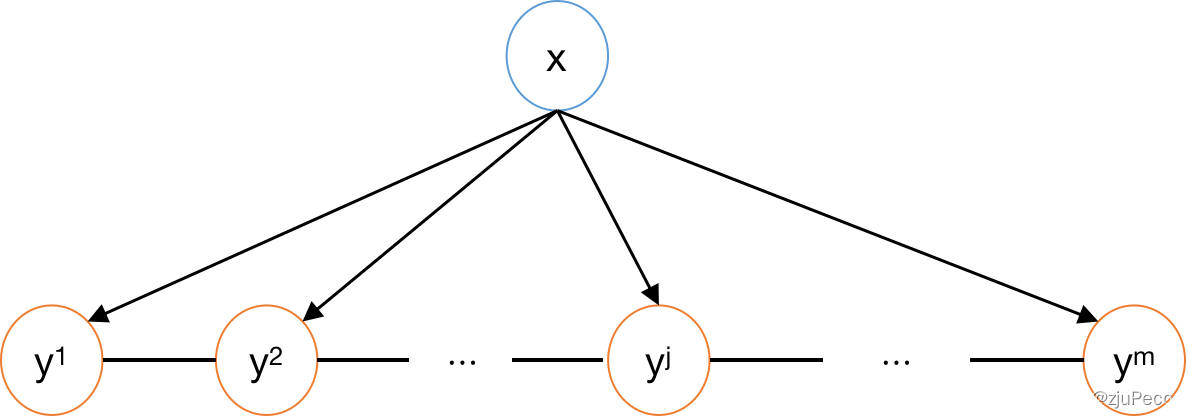
CRF的概率图模型如下图4-1所示，它和图3-1的区别是，$y^j$之间变成了无向图。还是那句话，不看这个图也没问题。

图4-1 CRF概率图

4.2 模型训练

CRF的模型训练和log-linear模型的方法基本一致。简而言之，就是我们有$n$条训练样本 { ( x ˉ i , y ˉ i ) } i = 1 n \{(\bar{x}_i, \bar{y}_i)\}_{i=1}^n {(xˉi​,yˉ​i​)}i=1n​，每个${\bar{x}}_i$都是序列$x_i^1,...,x_i^m$，每个${\bar{y}}_i$也都是序列$y_i^1,...,y_i^m$。

其目标函数为

$${\bar{w}}^{\ast }=arg\underset{\bar{w}}{\max }\sum _{i=1}^{n}log(p({\bar{y}}_i|{\bar{x}}_i;\bar{w}))-\frac{\lambda }{2}||\bar{w}|{|}^2\text{\hspace{1em}(4-4)}$$

接下来的任务就交给梯度下降就可以了。

4.3 模型解码

CRF进行decoding目标是

$$\begin{array}{rl}arg\underset{\bar{y}\in Y^m}{\max }p(\bar{y}|\bar{x};\bar{w})& =arg\underset{\bar{y}\in Y^m}{\max }\frac{exp(\bar{w}\cdot \bar{\Phi }(\bar{x},\bar{y}))}{{\sum }_{y^{\prime }\in Y}exp(\bar{w}\cdot \bar{\Phi }(\bar{x},{\bar{y}}^{\prime }))}\\ & =arg\underset{\bar{y}\in Y^m}{\max }exp(\bar{w}\cdot \bar{\Phi }(\bar{x},\bar{y}))\\ & =arg\underset{\bar{y}\in Y^m}{\max }\bar{w}\cdot \bar{\Phi }(\bar{x},\bar{y})\\ & =arg\underset{\bar{y}\in Y^m}{\max }\sum _{j=1}^m\bar{w}\cdot \bar{\varphi }(\bar{x},j,y^{j-1},y^j)\end{array}\text{\hspace{1em}(4-5)}$$

$\bar{\varphi }(\bar{x},j,y^{j-1},y^j)$有一部分是和$y^{j-1}$有关的，称为转移特征；还有一部分是和$y^{j-1}$无关的，称为状态特征。这里杂到一起了，可以不用关心。

解码的方法还是用的动态规划，同样定义一个$\pi [j,s]$。

初始概率为

$$\pi [1,y]=\bar{w}\cdot \bar{\varphi }(\bar{x},1,y^0,y)\text{\hspace{1em}(4-6)}$$

概率的迭代式为

$$\pi [j,y]=\underset{y^{\prime }\in Y}{\max }(\pi [j-1,y^{\prime }]+\bar{w}\cdot \bar{\varphi }(\bar{x},j,y^{\prime },y))\text{\hspace{1em}(4-6)}$$

求出所有的$\pi [j,y]$之后，就可以得到概率最大的那条路径

$$\underset{y^1,...,y^m}{\max }\sum _{j=1}^m\bar{w}\cdot \varphi (\bar{x},j,y^{j-1},y^j)=\underset{y}{\max }\pi [m,s]\text{\hspace{1em}(4-7)}$$

4.4 小结

CRF既解决了HMM观测独立不合理的问题，也解决的MEMM中label bias的问题，并且可以手动加入特征函数来干预模型的输出，有些不可能的情况，可以手动把转移概率设得很小即可。

一般会把CRF加在Bi-LSTM之后，让序列模型的输出更可控。如果数据够多，且够均衡的话，CRF也是可以不加的。

参考资料

[1] Log-Linear Models, MEMMs, and CRFs
[2] https://anxiang1836.github.io/2019/11/05/NLP_From_HMM_to_CRF/
[3] https://pytorch.org/tutorials/beginner/nlp/advanced_tutorial.html
[4] https://www.bilibili.com/video/BV19t411R7QU?p=4&share_source=copy_web
[5] The Label Bias Problem