必备的数学知识

DirectXMath库：如下所示：
1.对于Windows 8及其以上版本来讲，DirectXMath库是一款为Direct3D应用程序量身打造的3D数学库，而它也自此成为了Windows SDK的一部分。
2.DirectXMath库采用了SSE2指令集。借助128位宽的SIMD寄存器，利用一条SIMD指令即可同时对4个32位浮点数或整数进行运算。
3.使用DirectXMath库需要满足以下条件：
1>.所有平台需要启用SSE2指令集以及快速浮点模型。如图所示：2>.需要向代码中添加DirectX命令空间中记录相关数学操作的头文件DirectXMath.h以及DirectX::PackedVector命名空间中记录相关数据类型的的头文件DirectXPackedVector.h。
4.关于DirectXMath库的所有细节，可以参考DirectXMath programming reference。
5.关于DirectXMath库的设计原理，可以参考Designing Fast Cross-Platform SIMD Vector Libaries。

向量代数：如下所示：
1.向量可以用来模拟同时具有大小和方向的物理量。在几何学上，我们用有向线段来表示向量。其中线段长度代表向量的大小，线段箭头的指向代表向量的方向。
2.当向量平移至尾部与所在坐标系原点恰好重合的位置时，向量位于标准位置。一旦向量处于标准位置，我们便可以用向量头部相对于坐标系的坐标来作为它的数学描述。
3.改变向量的位置并不会对其大小和方向这两个属性造成任何影响，因此两个向量相等就等价于它们的大小相等且方向相同。
4.假设向量u = (a, b, c)和向量v = (i, j, k)，那么就能对它们进行下列向量计算：
1>.加法运算：u + v = (a + i, b + j, c + k)。
2>.减法运算：u - v = (a - i, b - j, c - k)。
3>.标量乘法运算：ku = (ka, kb, kc)。
4>.向量长度：||u|| = √a² + b² + c²。
5>.规范化：û = u / ||u|| = (a / |u||, b / |u||, c / |u||)。
6>.点积：u · v = ||u|| ||v|| cosθ = ai + bj + ck。
7>.叉积：u x v = (bk - cj, ci - ak, aj - bi)。
8>.u在v方向上的正交投影为：p = PROJv(u) = (||u|| cosθ)v = (||u|| ·1cosθ)v = (||u|| ||v|| cosθ)v = (u · v)v = (u · v / ||v||)v / ||v|| = ((u · v) / ||v||²)v。
5.为了在代码中利用SIMD技术进行高效运算，可以使用DirectXMath库的XMVECTOR类型来描述向量；使用XMVECTORF32 / XMVECTORU32类型来描述常向量。其中XMVECTOR类型具有以下特性：
1>.XMVECTOR类型的数据需要按照16字节对齐。其中局部变量和全局变量可以自动实现这种对齐；但是对于类中的数据成员来说，就需要使用XMFLOAT2 / XMFLOAT3 / XMFLOAT4类型来表示向量，并通过加载方法(XMLoadFloat)和存储方法(XMStoreFloat)令数据在XMVECTOR类型与XMFLOAT2 / XMFLOAT3 / XMFLOAT4类型之间互相转换。
2>.当XMVECTOR类型的值被当做参数传入函数时，可以直接存入SSE/SSE2寄存器中而不是栈上。要令代码与平台无关，我们将使用FXMVECTOR，GXMVECTOR，HXMVECTOR和CXMVECTOR类型来传递XMVECTOR参数。当函数为构造函数时，传递XMVECTOR参数的规则为：前3个XMVECTOR参数应当用FXMVECTOR类型，其余的XMVECTOR参数则用CXMVECTOR类型；当函数为普通函数时，传递XMVECTOR参数的规则为：前3个XMVECTOR参数应当用FXMVECTOR类型，第4个XMVECTOR参数用GXMVECTOR 类型，第5个和第6个XMVECTOR参数用HXMVECTOR类型，其余的XMVECTOR参数则用CXMVECTOR类型。
3>.XMVECTOR类型重载了一些运算符用来实现向量的加法，减法和标量乘法。
6.DirectXMath库中提供的向量相关辅助函数如下所示：

// 特别说明：
// 1.将XM_CALLCONV调用约定注解加在非构造函数名之前时，它会根据编译器的版本确定出对应的调用约定属性。
// 2.为了将标量和SIMD向量的混合运算次数降到最低，使用户除了自定义的计算之外全部都使用SIMD技术，以提升计算效率，此时可以将标量复制到SIMD向量的每个分量中去来实现。

// 将数据从XMFLOAT2类型中加载到XMVECTOR类型
(XMVECTOR XM_CALLCONV XMLoadFloat2(const XMFLOAT2 *pSource));
// 将数据从XMFLOAT3类型中加载到XMVECTOR类型
(XMVECTOR XM_CALLCONV XMLoadFloat3(const XMFLOAT3 *pSource));
// 将数据从XMFLOAT4类型中加载到XMVECTOR类型
(XMVECTOR XM_CALLCONV XMLoadFloat4(const XMFLOAT4 *pSource));

// 将数据从XMVECTOR类型中加载到XMFLOAT2类型
void XM_CALLCONV XMStoreFloat2(XMFLOAT2 *pDestination, FXMVECTOR V);
// 将数据从XMVECTOR类型中加载到XMFLOAT3类型
void XM_CALLCONV XMStoreFloat3(XMFLOAT3 *pDestination, FXMVECTOR V);
// 将数据从XMVECTOR类型中加载到XMFLOAT4类型
void XM_CALLCONV XMStoreFloat4(XMFLOAT4 *pDestination, FXMVECTOR V);

// 从XMVECTOR实例中得到某一向量的x分量
float XM_CALLCONV XMVectorGetX(FXMVECTOR V);
// 从XMVECTOR实例中得到某一向量的y分量
float XM_CALLCONV XMVectorGetY(FXMVECTOR V);
// 从XMVECTOR实例中得到某一向量的z分量
float XM_CALLCONV XMVectorGetZ(FXMVECTOR V);
// 从XMVECTOR实例中得到某一向量的w分量
float XM_CALLCONV XMVectorGetW(FXMVECTOR V);

// 将某一向量的x分量转换为XMVECTOR类型
XMVECTOR XM_CALLCONV XMVectorSetX(FXMVECTOR V, float x);
// 将某一向量的y分量转换为XMVECTOR类型
XMVECTOR XM_CALLCONV XMVectorSetY(FXMVECTOR V, float y);
// 将某一向量的z分量转换为XMVECTOR类型
XMVECTOR XM_CALLCONV XMVectorSetZ(FXMVECTOR V, float z);
// 将某一向量的w分量转换为XMVECTOR类型
XMVECTOR XM_CALLCONV XMVectorSetW(FXMVECTOR V, float w);

// 将角度转换成弧度
inline float XMConvertToRadians(float fDegrees);
// 将弧度转换成角度
inline float XMConvertToDegrees(float fRadians);

// 返回零向量0
XMVECTOR XM_CALLCONV XMVectorZero();
// 返回向量(1, 1, 1, 1)
XMVECTOR XM_CALLCONV XMVectorSplatOne();
// 返回向量(x, y, z, w)
XMVECTOR XM_CALLCONV XMVectorSet(float x, float y, float z, float w);
// 返回向量(value, value, value, value)
XMVECTOR XM_CALLCONV XMVectorReplicate(float value);
// 返回向量(vx, vx, vx, vx)
XMVECTOR XM_CALLCONV XMVectorSplatX(FXMVECTOR V);
// 返回向量(vy, vy, vy, vy)
XMVECTOR XM_CALLCONV XMVectorSplatY(FXMVECTOR V);
// 返回向量(vz, vz, vz, vz)
XMVECTOR XM_CALLCONV XMVectorSplatZ(FXMVECTOR V);

// 返回||V||
XMVECTOR XM_CALLCONV XMVector3Length(FXMVECTOR V);
// 返回估算值||V||
XMVECTOR XM_CALLCONV XMVector3LengthEst(FXMVECTOR V);
// 返回||V||²
XMVECTOR XM_CALLCONV XMVector3LengthSq(FXMVECTOR V);
// 返回V1·V2
XMVECTOR XM_CALLCONV XMVector3Dot(FXMVECTOR V1, FXMVECTOR V2);
// 返回V1xV2
XMVECTOR XM_CALLCONV XMVector3Cross(FXMVECTOR V1, FXMVECTOR V2);
// 返回V/||V||
XMVECTOR XM_CALLCONV XMVector3Normalize(FXMVECTOR V);
// 返回估算值V/||V||
XMVECTOR XM_CALLCONV XMVector3NormalizeEst(FXMVECTOR V);
// 返回一个正交与V的向量
XMVECTOR XM_CALLCONV XMVector3Orthogonal(FXMVECTOR V);
// 返回V1和V2之间的夹角
XMVECTOR XM_CALLCONV XMVector3AngleBetweenVectors(FXMVECTOR V1, FXMVECTOR V2);
// 返回参数pParaller：表示V在Normal上的投影
// 返回参数pPerpendicular：表示V在Normal正交方向上的投影
// 输入参数Normal：表示规范化向量
void XM_CALLCONV XMVector3ComponentsFromNormal(XMVECTOR* pParaller, XMVECTOR* pPerpendicular, FXMVECTOR V, FXMVECTOR Normal);
// 返回V1是否等于V2
bool XM_CALLCONV XMVector3Equal(FXMVECTOR V1, FXMVECTOR V2);
// 返回V1是否不等于V2
bool XM_CALLCONV XMVector3NotEqual(FXMVECTOR V1, FXMVECTOR V2);
// 用于以Epsilon作为容差，测试比较的向量是否近似相等。等价于：
// abs(U.x - V.x) <= Epsilon.x &&
// abs(U.y - V.y) <= Epsilon.y &&
// abs(U.z - V.z) <= Epsilon.z
// 其中Epsilon一般为(0.001f, 0.001f, 0.001f)
XMFINLINE bool XM_CALLCONV XMVector3NearEqual(FXMVECTOR U, FXMVECTOR V, FXMVECTOR Epsilon)

矩阵代数：如下所示：
1.m x n矩阵M是一个由m行n列实数所构成的矩形阵列。
2.当两个矩阵维度相同且对应的元素分别相等时，这两个矩阵才相等。
3.两个同维矩阵的加法运算是将两个矩阵对应的元素相加来实现。
4.标量与矩阵的乘法运算是将标量与矩阵中每个元素分别相乘。
5.如果A是一个m x n矩阵，且B为一个n x p矩阵，那么两者乘积AB的结果是一个规模为m x p的矩阵C。矩阵C中的第i行，第j列的元素，由矩阵A中的第i个行向量与矩阵B中的第j个列向量进行点积运算得出，即Cij = Ai,* · B*,j。
6.矩阵乘法不满足交换律(即一般来说，AB ≠ BA)，但是却满足结合律(AB)C = A(BC)。对于一个1 x n行向量u与一个n x m矩阵A，我们总可以得到u所给出的标量系数与A中诸行向量的线性组合uA：7.转置矩阵由原矩阵互换行与列来求得。所以，m x n矩阵的转置矩阵为n x m矩阵。
8.单位矩阵是一种除主对角线上的元素为1外，其他元素均为0的方阵。任何矩阵与单位矩阵相乘，得到的依然是原矩阵。
9.假设A为一个n x n矩阵。则有：
1>.余子阵▔Aij即为从A中去除第i行和第j列的(n - 1)x(n - 1)矩阵。
2>.行列式det A是一种特殊的函数，向它传入一个方阵便会就算出一个对应的实数。当n > 1时，det A计算公式为:

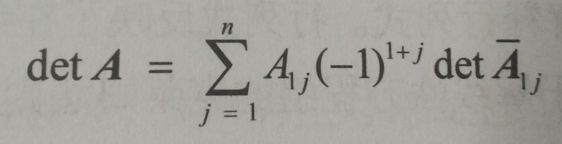
3>.元素Aij的代数余子式为：

4>.矩阵A的代数余子式矩阵为：

5>.矩阵A的伴随矩阵为：

6>.矩阵A的逆矩阵为：

其中矩阵与其逆矩阵的乘积结果为单位矩阵。如果一个矩阵是可逆的，则此矩阵的逆矩阵是唯一的。只有方阵才可能有逆矩阵。
10.我们在编写代码时，要用DirectX库中的XMMATRIX类型来表示4x4矩阵。它的特性如下所示：
1>.由于XMMATRIX类型内部是由4个XMVECTOR类型实例所构成，所以XMMATRIX类型可以使用SIMD技术高效的运算能力。
2>.XMMATRIX类型的数据需要按照16字节对齐。其中局部变量和全局变量可以自动实现这种对齐；但是对于类中的数据成员来说，就需要使用XMFLOAT4X4类型来加以表示，并通过加载(XMLoadFloat4x4)和存储(XMStoreFloat4x4)方法，使数据在XMMATRIX类型与XMFLOAT4X4类型之间互相转换。
3>.当函数为构造函数时，需要使用CXMMATRIX类型来获取XMMATRIX类型参数；当函数为普通函数时，假设传入函数的FXMVECTOR参数不超过两个，则第一个XMMATRIX参数应该用FXMMATRIX类型，其余的XMMATRIX参数均应该为CXMMATRIX类型。
4>.XMMATRIX类型重载了一些算数运算符，使矩阵可以实现加法运算，减法运算，矩阵乘法运算和标量乘法运算。
11.DirectXMath库中提供的矩阵相关辅助函数如下所示：

// 将16个浮点数据转换成XMMATRIX类型实例
XMMATRIX XM_CALLCONV XMMatrixSet(
  float m00, float m01, float m02, float m03,
  float m10, float m11, float m12, float m13,
  float m20, float m21, float m22, float m23,
  float m30, float m31, float m32, float m33);

// 将数据从XMFLOAT4X4类型中加载到XMMATRIX类型
inline XMMATRIX XM_CALLCONV XMLoadFloat4x4(const XMFLOAT4X4* pSource);
// 将数据从XMMATRIX类型中存储到XMFLOAT4X4类型
inline void XM_CALLCONV XMStoreFloat4x4(XMFLOAT4X4* pDestination, FXMMATRIX M);
// 返回单位矩阵I
XMMATRIX XM_CALLCONV XMMatrixIdentity();
// 返回矩阵M是否为单位矩阵
bool XM_CALLCONV XMMatrixIsIdentity(FXMMATRIX M);
// 返回矩阵乘积AB
XMMATRIX XM_CALLCONV XMMatrixMultiply(FXMMATRIX A, CXMMATRIX B);
// 返回矩阵M的转置矩阵
XMMATRIX XM_CALLCONV XMMatrixTranspose(FXMMATRIX M);
// 返回矩阵M的行列式det M，并存储到XMVECTOR类型变量中，以便充分利用SIMD技术高效的运算能力。
XMVECTOR XM_CALLCONV XMMatrixDeterminant(FXMMATRIX M);  
// 返回矩阵M的逆矩阵
XMMATRIX XM_CALLCONV XMMatrixInverse(XMVECTOR* pDeterminant, FXMMATRIX M);

几何变换：如下所示：
1.标准基向量指的是坐标轴正方向上的单位向量。如：x轴上的(1, 0, 0)，y轴上的(0, 1, 0)以及z轴上的(0, 0, 1)。
2.假设函数τ(μ) = τ(x, y, z) = (x′, y′, z′)，当τ为线性变换时，此函数具有以下性质：
1>.τ(μ + v) = τ(μ) + τ(v)。
2>.τ(kμ) = kτ(μ)。
3>.τ(aμ + bv + cw) = aτ(μ) + bτ(v) + cτ(w)。
4>.τ(μ) = xτ(i) + yτ(j) + zτ(k) = μA = [x, y, z] [A11, A12, A13, A21, A22, A23, A31, A32, A33]。
其中μ = (x, y, z)，τ(i) = (A11, A12, A13)，τ(j) = (A21, A22, A23)以及τ(k) = (A31, A32, A33)时，矩阵A就是线性变换τ的矩阵表示法。
3.仿射变换为一个线性变换加上一个平移向量。对应的数学表达式为：
α(μ) = τ(μ) + b = μA + b = [x, y, z, 1][A11, A12, A13, 0, A21, A22, A23, 0, A31, A32, A33, 0, bx, by, bz, 1] = [x′, y′, z′, 1]。
其中μ = (x, y, z, 1)，b = ( bx, by, bz, 1)时，矩阵A就是仿射变换的矩阵表示法。
4.缩放，平移和旋转这3种基本操作的变换矩阵分别为：
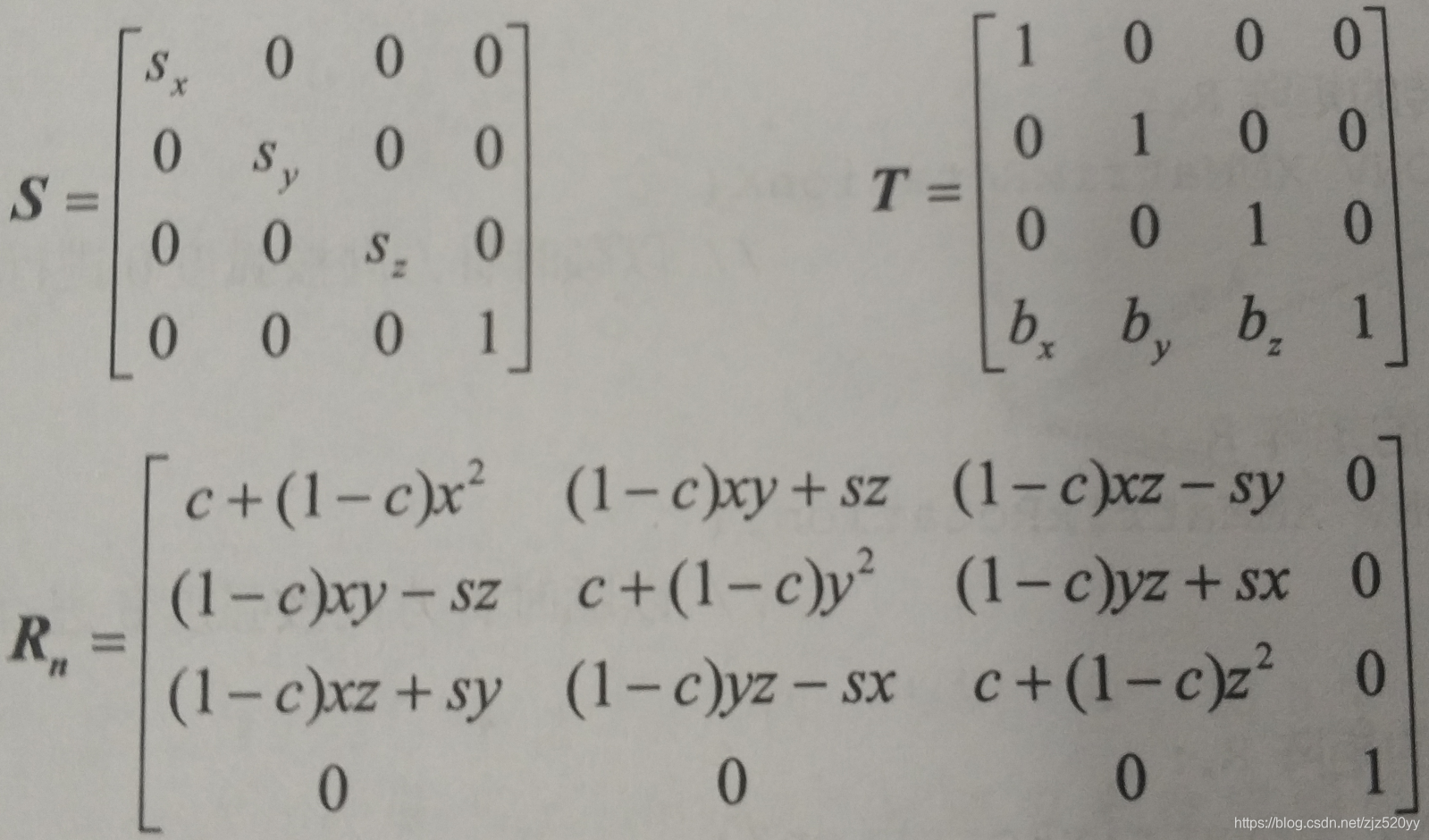其中c=cosθ且s=sinθ。
5.如果一个矩阵内所有的行向量都是单位长度且两两相交，则此矩阵为正交矩阵。正交矩阵有个特殊性质：它的逆矩阵与转置矩阵相等。因此，这使它的逆矩阵计算起来方便且高效。另外，所有的旋转矩阵皆为正交矩阵。
6.我们通过4 x 4矩阵来表示变换，并利用1 x 4齐次坐标来描述点和向量：当把第4个分量设置为w=1时，表示点；设置为w=0时，则表示向量。这样一来，平移操作将只应用于点，而不会影响向量。
7.由于矩阵的乘法运算满足结合律，因此我们就能够将若干种变换矩阵合而为一。此矩阵给予物体的变换效果，与合成它的多个单一矩阵对物体按次序进行变换的净效果相同。
8.设qb，ub，vb和wb分别表示坐标系A中的原点，x轴，y轴，z轴相对于坐标系B的坐标。如果一个向量或者点p相对于坐标系A的坐标为pa = (x, y, z)，那么，此同一向量或者点相对于坐标系B的坐标为：
1>.针对向量而言：pb = (x′, y′, z′) = xub + yvb + zwb。
2>.针对点而言：pb = (x′, y′, z′) = xub + yvb + zwb + qb。
3>.针对点和向量而言：pb = (x′, y′, z′, w) = xub + yvb + zwb + wqb。如果w = 1，此式化简为点的坐标变换公式；如果w = 0，则此式化简为向量的坐标变换公式。当ub = (ux, uy, uz, 0)，vb = (vx, vy, vz, 0)，wb = (wx, wy, wz, 0)以及qb = (qx, qy, qz, 1)时，此时坐标系A中的坐标转换为坐标系B中的坐标的变换矩阵为：

9.假设有3个坐标系F，G和H。已知将坐标由F转换到G的坐标系变换矩阵为A，把坐标由G转换到H的坐标系变换矩阵为B。根据矩阵与矩阵的乘法运算法则，可以将矩阵乘积C = AB看作把坐标由F直接转换到H的坐标系变换矩阵。这就是说，利用矩阵之间的乘法运算，能够将矩阵A和矩阵B的变换效果组合为一个净矩阵，并可记作pF(AB) = pH。
10.如果矩阵M可以将坐标从坐标系A映射至坐标系B，那么矩阵M的逆矩阵则能够将坐标由坐标系B映射到坐标系A。
11.我们能够将一个改变几何体的复合变换(缩放，旋转和平移)，解释为一种对应的坐标变换。
12.DirectXMath库中提供的变换相关辅助函数如下所示：

// 特别说明：
// 1.当沿旋转轴向原点的方向来观察时，按顺时针方向来测定旋转角(也就是在左手坐标系中，从旋转轴负方向来看，以顺时针方向作为旋转的正方向)。

// 用缩放系数来构建一个缩放矩阵
XMMATRIX XM_CALLCONV XMMatrixScaling(float ScaleX, float ScaleY, float ScaleZ);
// 用一个3D向量中的分量来构建一个缩放矩阵
XMMATRIX XM_CALLCONV XMMatrixScalingFromVector(FXMVECTOR Scale);
// 构建一个绕X轴旋转的矩阵
XMMATRIX XM_CALLCONV XMMatrixRotationX(float Angle);
// 构建一个绕Y轴旋转的矩阵
XMMATRIX XM_CALLCONV XMMatrixRotationY(float Angle);
// 构建一个绕Z轴旋转的矩阵
XMMATRIX XM_CALLCONV XMMatrixRotationZ(float Angle);
// 构建一个绕任意轴旋转的矩阵
XMMATRIX XM_CALLCONV XMMatrixRotationAxis(FXMVECTOR Axis, float Angle);
// 用平移系数来构建一个平移矩阵
XMMATRIX XM_CALLCONV XMMatrixTranslation(float OffsetX, float OffsetY, float OffsetZ);
// 用一个3D向量中的分量来构建一个平移矩阵
XMMATRIX XM_CALLCONV XMMatrixTranslationFromVector(FXMVECTOR Offset);
// 计算向量与矩阵的乘积vM,此函数为针对点的变换，即总是默认令Vw = 1
XMVECTOR XM_CALLCONV XMVector3TransformCoord(FXMVECTOR V, FXMMATRIX M);
// 计算向量与矩阵的乘积vM,此函数为针对向量的变换，即总是默认令Vw = 0
XMVECTOR XM_CALLCONV XMVector3TransformNormal(FXMVECTOR V, FXMMATRIX M);