比萨斜塔——统计显著性检验

最新推荐文章于 2023-11-27 14:19:14 发布

mmい

最新推荐文章于 2023-11-27 14:19:14 发布

阅读量3.5k

点赞数

分类专栏： Machine Learning

本文链接：https://blog.csdn.net/zm714981790/article/details/51245502

版权

本文通过比萨斜塔的倾斜数据，探讨了线性回归模型的建立、残差分析、R-Squared统计量以及T分布下的统计显著性检验，解释了如何判断倾斜程度与年份之间的显著相关性。

摘要由CSDN通过智能技术生成

Dataset

比萨斜塔是意大利最大的旅游景点之一。几百年来这座塔慢慢靠向一边,最终达到5.5度的倾斜角度，在顶端水平偏离了近3米。年度数据pisa.csv文件记录了从1975年到1987年测量塔的倾斜，其中lean代表了偏离的角度。在这个任务,我们将尝试使用线性回归来估计倾斜率以及解释其系数和统计数据。

这里写图片描述

# 读取数据
import pandas
import matplotlib.pyplot as plt
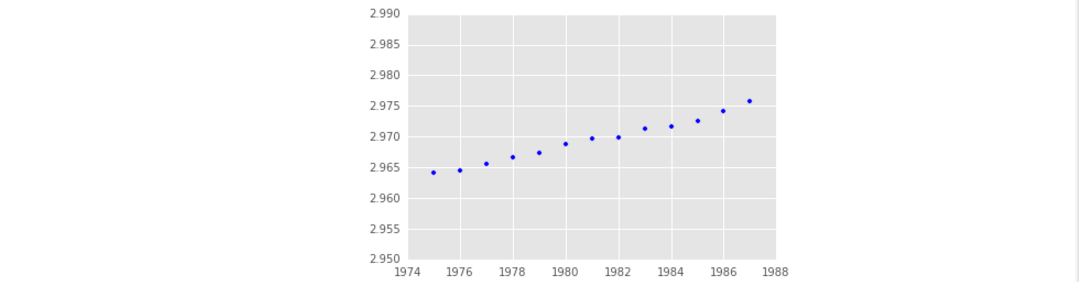
pisa = pandas.DataFrame({"year": range(1975, 1988), 
                         "lean": [2.9642, 2.9644, 2.9656, 2.9667, 2.9673, 2.9688, 2.9696, 
                                  2.9698, 2.9713, 2.9717, 2.9725, 2.9742, 2.9757]})

print(pisa)
'''
      lean  year
0   2.9642  1975
1   2.9644  1976
2   2.9656  1977
3   2.9667  1978
4   2.9673  1979
5   2.9688  1980
6   2.9696  1981
7   2.9698  1982
8   2.9713  1983
9   2.9717  1984
10  2.9725  1985
11  2.9742  1986
12  2.9757  1987
'''
plt.scatter(pisa["year"], pisa["lean"])

这里写图片描述

Fit The Linear Model

从散点图中我们可以看到用曲线可以很好的拟合该数据。在之前我们利用线性回归来分析葡萄酒的质量以及股票市场，但在这个任务中，我们将学习如何理解关键的统计学概念。Statsmodels是Python中进行严格统计分析的一个库，对于线性模型，Statsmodels提供了足够多的统计方法以及适当的评估方法。sm.OLS这个类用于拟合线性模型，采取的优化方法是最小二乘法。OLS()不会自动添加一个截距到模型中，但是可以自己添加一列属性，使其值都是1即可产生截距。

import statsmodels.api as sm

y = pisa.lean # target
X = pisa.year  # features
# add a column of 1's as the constant term
X = sm.add_constant(X)  

# OLS -- Ordinary Least Squares Fit
linear = sm.OLS(y, X)
# fit model
linearfit = linear.fit()
print(linearfit.summary())
'''
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                   lean   R-squared:                       0.988
Model:                            OLS   Adj. R-squared:                  0.987
Method:                 Least Squares   F-statistic:                     904.1
Date:                Mon, 25 Apr 2016   Prob (F-statistic):           6.50e-12
Time:                        13:30:20