关于PID控制器的理解

关于PID控制器的理解

P比例控制

• 比例控制着眼于当前误差, 是将当前误差乘以一个比例系数, 得到的值即为系统下个时刻的输入, 原理图如下:
  
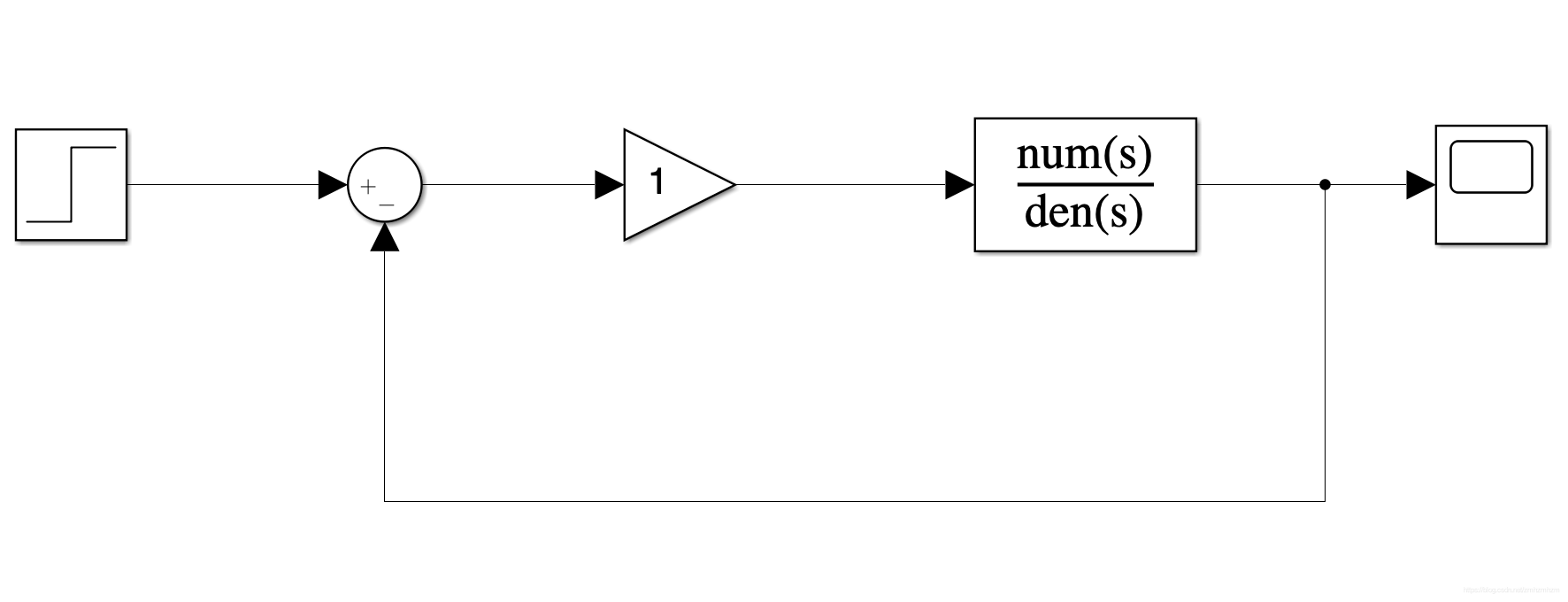
  但只用比例控制器可能会出现稳态误差不为零的情况, 并且可能会出现震荡情况, 如下图所示:
  
  参考值为阶跃函数, 阶跃幅值为1, 但稳定后的结果为0.5, 因此存在稳态误差。当然, 有些系统对于阶跃信号, 只用比例控制器控制也不会存在稳态误差, 比如I型系统与II型系统, 详细说明可参考https://blog.csdn.net/zmhzmhzm/article/details/105994024

  如果系统只用比例控制器, 并且存在稳态误差的话, 可以考虑加入积分控制器, 积分项可消除稳态误差, 组合起来即为比例积分控制器。 如果有震荡的话可以考虑加入微分控制器, 组合起来即为比例微分控制器

• C++代码实现

  double PidOutput(const double& ref, const double& now)
  {
  	double Kp = 1.0;
  	double output = 0.0;
  	output = Kp * (ref - now);
  	return output;
  }
  

PI比例积分控制

• 比例积分控制的积分项, 着眼于过去误差的累计, 可以帮助消除稳态误差, 原理图如下:
  
  使用比例积分控制可消除稳态误差, 但仍存在震荡的情况, 如下图所示:
  
  若想消除抖动, 则需加入微分控制器, 组合起来即为比例积分微分控制器(PID控制器)

• C++代码实现

  double dt = 0.01;
  double err_sum = 0.0;
  double err = 0.0;
  double Kp = 1.0;
  double Ki = 1.0;
  double output = 0.0;
  
  double PidOutput(const double& ref, const double& now)
  {
  	err = ref - now;
  	err_sum += (err_ * dt);
  	output = Kp * err + ki * (err_sum);
  	return output;
  }
  

PD比例微分控制

• 比例微分控制的微分项, 着眼于误差的变化趋势, 可以在误差收敛过快的情况下减小系统的输入已达到减少超调的目的, 可以帮助减少震荡, 原理图如下:
  
  使用比例微分控制可减少震荡, 但仍存在稳态误差, 如下图所示:
  
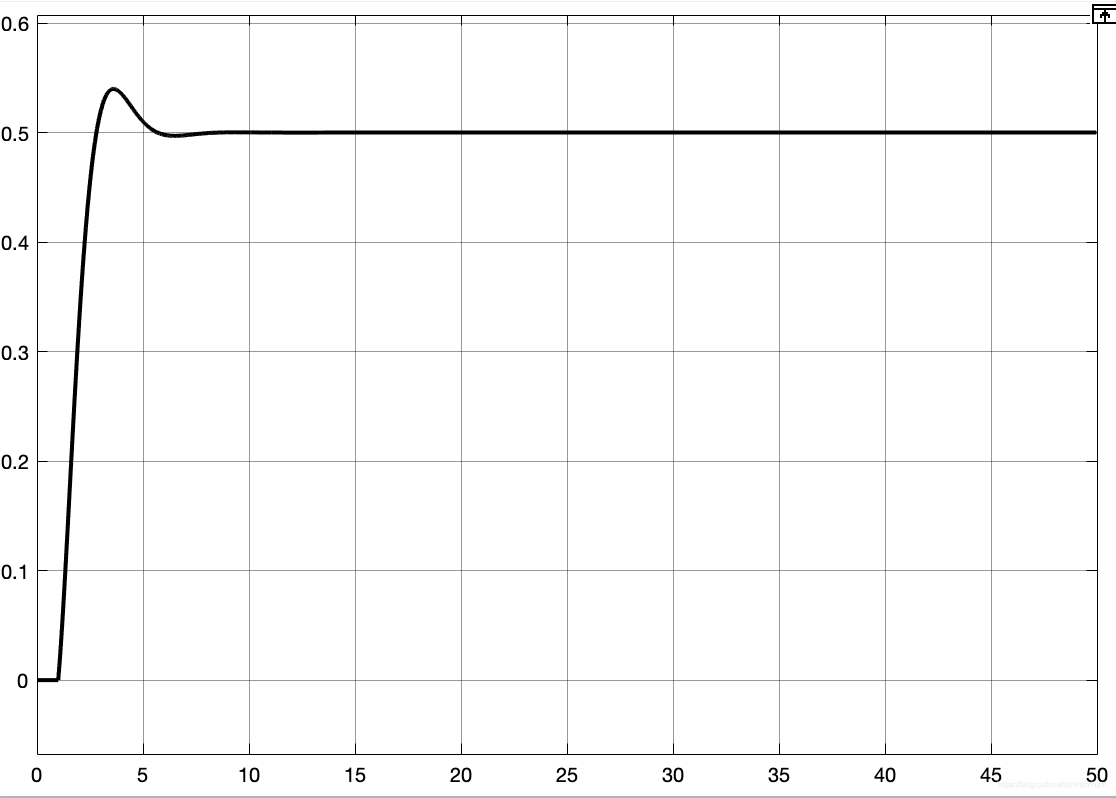
  可以看出参考值阶跃函数幅值为1, 但稳定后的结果为0.5, 因此存在稳态误差。若想消除稳态误差, 则需要加入积分控制器, 组合起来即为比例积分微分控制器(PID控制器)

• 微分控制器注意事项!!!

  比例微分控制器虽然能减少系统震荡, 但其对高频信号十分敏感, 假设比例微分控制器的传递函数为$G(s)=1+s$, 画出其伯德图为:
  
  从图中可看出, 随着频率增大, 幅值增益增大, 因此比例微分控制器会放大高频信号, 对高频信号敏感

  • 数学解释:
    假设高频信号为$f(t)=0.001sin(1000\omega t)$, 对$f(t)$求微分可得 $\frac{df(t)}{dt}=cos(1000\omega t)$, 可见即便高频信号幅值一开始很小, 但求完微分后, 信号幅值仍被放大了1000倍, 所以微分对高频敏感

• C++代码实现

  double dt = 0.01;
  double err_old = 0.0;
  double err = 0.0;
  double Kp = 1.0;
  double Kd = 1.0;
  double output = 0.0;
  
  double PidOutput(const double& ref, const double& now)
  {
  	err_old = err;
  	err = ref - now;
  	output = Kp * err + Kd * (err - err_old) / dt;
  	return output;
  }
  

PID比例积分微分控制

• 比例积分微分控制同时着眼于当前误差, 过去误差的累计, 和误差变化的趋势, 既可以消除稳态误差, 也可以减少系统震荡, 原理图如下:
  
  系统表现结果如下:
  
  虽然PID控制综合表现最好, 但因为存在微分项, 所以仍会存在PD控制器的对高频信号敏感的问题

• C++代码实现

  double dt = 0.01;
  double err_sum = 0.0;
  double err_old = 0.0;
  double err = 0.0;
  double Kp = 1.0;
  double Ki = 1.0;
  double Kd = 1.0;
  double output = 0.0;
  
  double PidOutput(const double& ref, const double& now)
  {
  	err_old = err;
  	err = ref - now;
  	err_sum += (err_ * dt);
  	output = Kp * err + Ki * err_sum + Kd * (err - err_old) / dt;
  	return output;
  }
  

总结

比例控制器可收敛当前误差, 积分控制器可消除稳态误差, 微分控制器可减少震荡, 三种控制器可自由组合, 其中PID控制器效果最好, 但因为加入了微分项, 所以会对高频信号敏感, 一般PID全用到的情况不多, 能用PI解决的就不用PID解决了, 要用PID的话建议不要将D的参数调的过大, 否则系统会对高频信号(测量噪声)异常敏感