sdut 3256 BIGZHUGOD and His Friends II

BIGZHUGOD and His Friends II

Time Limit: 1000ms   Memory limit: 65536K  有疑问？点这里^_^

题目描述

BIGZHUGOD and his three friends are playing a game in a triangle ground.

The number of BIGZHUGOD is 0, and his three friends are numbered from 1 to 3. Before the game begins, three friends stand on three vertices of triangle in numerical order (1 on A, 2 on B, 3 on C), BIGZHUGOD stands inside of triangle.

Then the game begins, three friends run to the next vertex in uniform speed and in straight direction (1 to B, 2 to C, 3 to A and there speeds may different). And BIGZHUGOD can stand in any position inside the triangle.

When any of his friends arrives at next vertex, the game ends.

BIGZHUGOD and his friends have made an agreement: we assume that the beginning is time 0, if during the game, you can find a moment that BIGZHUGOD can block the sight line of 1 to C, 2 to A, 3 to B. Then each friend has to treat BIGZHUGOD with a big meal.

Now BIGZHUGOD knows the lengths of time that his three friends need run to next vertices t1, t2 and t3. He wants to know whether he has a chance to gain three big meals, of course he wants to know in which exciting moment t, he can block three friends\' sight line.

 

输入

 The first line contains an integer T, indicating the number of test cases (T ≤ 1000).

For each case there are three integer t1, t2, t3 (1 ≤ t1, t2, t3 ≤ 100).

 

输出

 If BIGZHUGOD has a chance to gain big meal from his friends, output "YES" and the exciting moment t rounding to 4 digits after decimal point. Otherwise, output "NO".

示例输入

2 
1 1 1 
3 4 6

示例输出

YES 0.5000 
YES 2.0000

提示

 

来源

 

示例程序

 

• 提交 
• 状态 
• 讨论
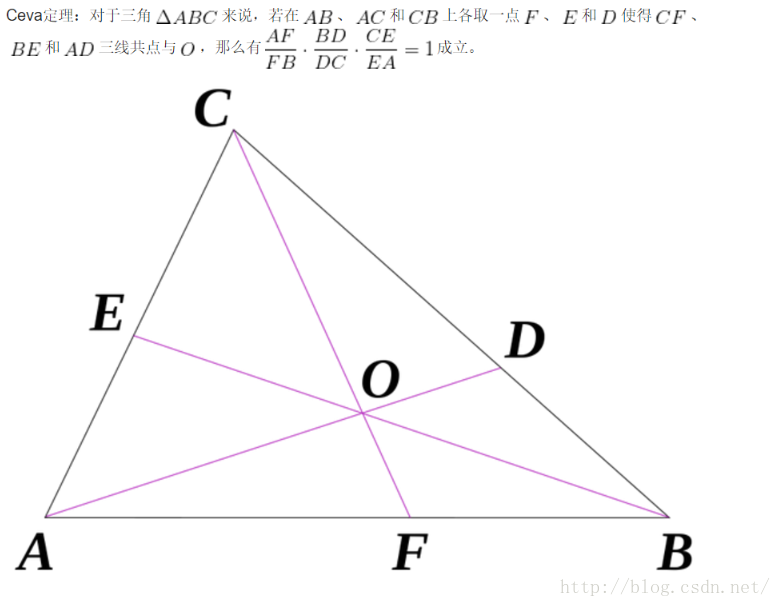
• • 有3个人在三角形的3个顶点ABC 他们分别以1/t1 1/t2 1/ t3 的速度从A->B B->C C->A的路径
  • 问有没有在某一时刻使得这3人与之对角的连线交与一点
  • 其实这就是赛瓦定理
  • 
    
  • 
    
• • 图片来至知乎
  • 知道这个定理后这题就很水了
  • 列个方程二分枚举下答案就好了
  • //精度搞错wa了好久还找程序对拍也没找出问题- - 太菜啦
  • ACcode:

  • #include <cstdio>
    #include <cmath>
    #define mid ((l+r)/2)
    int main(){
        int loop;
        scanf("%d",&loop);
        while(loop--){
            double l,r,tmp,t1,t2,t3;
            scanf("%d%d%d",&t1,&t2,&t3);
            l=0.0;r=t1>t2?t2:t1;r=r>t3?t3:r;
            while(fabs(r-l)>1e-8){
                tmp=2*mid*mid*mid-(t1+t2+t3)*mid*mid+(t1*t2+t2*t3+t1*t3)*mid-(t1*t2*t3);
                if(fabs(tmp)<1e-8)break;
                if(tmp>0)r=mid;
                else l=mid;
            }
            printf("YES %0.4f\n",mid);
        }
        return 0;
    }