【CFD理论】梯度项-LeastSquare Gradient-02
知识回顾:
扩散项 ⇒ ( ∇ ϕ ) f ⇒ ( ∇ ϕ ) p = 1 V P ∑ ϕ f S f 扩散项\Rightarrow(\nabla \phi)_f \Rightarrow (\nabla \phi)_p=\frac{1}{V_P}\sum \phi_f \boldsymbol S_f 扩散项⇒(∇ϕ)f⇒(∇ϕ)p=VP1∑ϕfSf
以温度为例 : ( ∇ T ) C = 1 V P ( T f 1 S f 1 + T f 2 S f 2 + T f 3 S f 3 + T f 4 S f 4 + T f 5 S f 5 + T f 6 S f 6 ) 以温度为例:(\nabla T)_C=\frac{1}{V_P}(T_{f1}\boldsymbol S_{f1}+T_{f2}\boldsymbol S_{f2}+T_{f3}\boldsymbol S_{f3}+T_{f4}\boldsymbol S_{f4}+T_{f5}\boldsymbol S_{f5}+T_{f6}\boldsymbol S_{f6}) 以温度为例:(∇T)C=VP1(Tf1Sf1+Tf2Sf2+Tf3Sf3+Tf4Sf4+Tf5Sf5+Tf6Sf6)
方法1:
(
∇
T
)
P
=
[
∂
T
∂
x
∂
T
∂
y
∂
T
∂
z
]
(\nabla T)_P= \left [ \begin{matrix} \frac{\partial T}{\partial x} \\ \frac{\partial T}{\partial y}\\ \frac{\partial T}{\partial z}\\ \end{matrix} \right ]
(∇T)P=⎣
⎡∂x∂T∂y∂T∂z∂T⎦
⎤
T
N
=
T
P
+
d
P
N
⋅
(
∇
T
)
P
T_N=T_P+\boldsymbol d_{PN}\cdot(\nabla T)_P
TN=TP+dPN⋅(∇T)P
ϕ
N
=
ϕ
P
+
(
∇
ϕ
)
P
⋅
(
r
N
−
r
P
)
\phi_N=\phi_P+(\nabla \phi)_P\cdot (\boldsymbol r_N-\boldsymbol r_P)
ϕN=ϕP+(∇ϕ)P⋅(rN−rP)
f
(
x
)
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
2
f(x)=f(x_0)+f'(x_0)(x-x_0)^2
f(x)=f(x0)+f′(x0)(x−x0)2
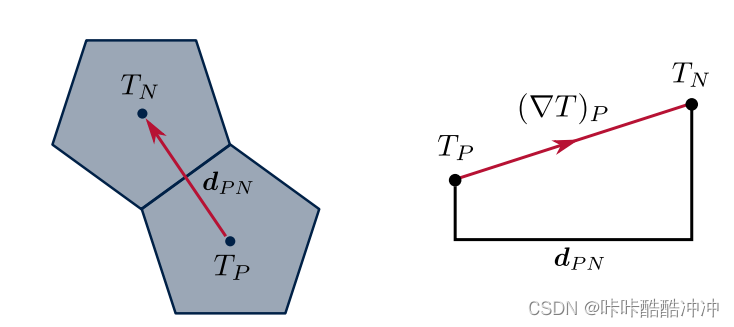
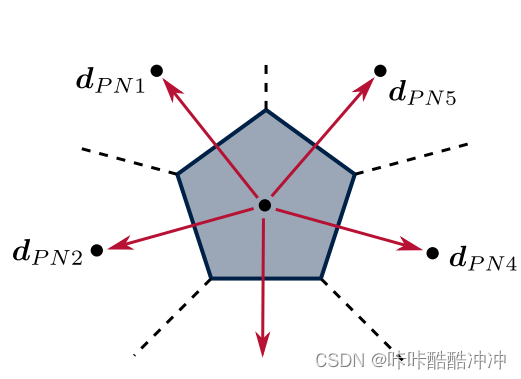
Least-Square Derivation
T
1
=
T
P
+
(
∇
T
)
P
⋅
d
P
N
1
T
2
=
T
P
+
(
∇
T
)
P
⋅
d
P
N
2
T
3
=
T
P
+
(
∇
T
)
P
⋅
d
P
N
3
T
4
=
T
P
+
(
∇
T
)
P
⋅
d
P
N
4
T
5
=
T
P
+
(
∇
T
)
P
⋅
d
P
N
5
T
6
=
T
P
+
(
∇
T
)
P
⋅
d
P
N
6
}
⇒
[
T
1
−
T
P
=
(
∇
T
)
P
⋅
r
P
N
1
T
2
−
T
P
=
(
∇
T
)
P
⋅
r
P
N
2
T
3
−
T
P
=
(
∇
T
)
P
⋅
r
P
N
3
T
4
−
T
P
=
(
∇
T
)
P
⋅
r
P
N
4
T
5
−
T
P
=
(
∇
T
)
P
⋅
r
P
N
5
T
6
−
T
P
=
(
∇
T
)
P
⋅
r
P
N
6
]
\left. \begin{array}{lll} T_1=T_P+(\nabla T)_P\cdot\boldsymbol d_{PN1}\\ T_2=T_P+(\nabla T)_P\cdot\boldsymbol d_{PN2}\\ T_3=T_P+(\nabla T)_P\cdot\boldsymbol d_{PN3}\\ T_4=T_P+(\nabla T)_P\cdot\boldsymbol d_{PN4}\\ T_5=T_P+(\nabla T)_P\cdot\boldsymbol d_{PN5}\\ T_6=T_P+(\nabla T)_P\cdot\boldsymbol d_{PN6}\\ \end{array} \right\} \Rightarrow \begin{aligned} \left [ \begin{matrix} T_1-T_P=(\nabla T)_P\cdot \boldsymbol r_{PN1} \\ T_2-T_P=(\nabla T)_P\cdot \boldsymbol r_{PN2} \\ T_3-T_P=(\nabla T)_P\cdot \boldsymbol r_{PN3} \\ T_4-T_P=(\nabla T)_P\cdot \boldsymbol r_{PN4} \\ T_5-T_P=(\nabla T)_P\cdot \boldsymbol r_{PN5} \\ T_6-T_P=(\nabla T)_P\cdot \boldsymbol r_{PN6} \\ \end{matrix} \right ] \end{aligned}
T1=TP+(∇T)P⋅dPN1T2=TP+(∇T)P⋅dPN2T3=TP+(∇T)P⋅dPN3T4=TP+(∇T)P⋅dPN4T5=TP+(∇T)P⋅dPN5T6=TP+(∇T)P⋅dPN6⎭
⎬
⎫⇒⎣
⎡T1−TP=(∇T)P⋅rPN1T2−TP=(∇T)P⋅rPN2T3−TP=(∇T)P⋅rPN3T4−TP=(∇T)P⋅rPN4T5−TP=(∇T)P⋅rPN5T6−TP=(∇T)P⋅rPN6⎦
⎤
[
d
P
N
1
,
x
,
d
P
N
1
,
y
,
d
P
N
1
,
z
d
P
N
2
,
x
,
d
P
N
2
,
y
,
d
P
N
2
,
z
d
P
N
3
,
x
,
d
P
N
3
,
y
,
d
P
N
3
,
z
d
P
N
4
,
x
,
d
P
N
4
,
y
,
d
P
N
4
,
z
d
P
N
5
,
x
,
d
P
N
5
,
y
,
d
P
N
5
,
z
d
P
N
6
,
x
,
d
P
N
6
,
y
,
d
P
N
6
,
z
]
[
∂
T
∂
x
∂
T
∂
y
∂
T
∂
z
]
=
[
T
1
−
T
P
T
2
−
T
P
T
3
−
T
P
T
4
−
T
P
T
5
−
T
P
T
6
−
T
P
]
\begin{aligned} \left [ \begin{matrix} \boldsymbol d_{PN1,x},& \boldsymbol d_{PN1,y},& \boldsymbol d_{PN1,z}\\ \boldsymbol d_{PN2,x},& \boldsymbol d_{PN2,y},& \boldsymbol d_{PN2,z}\\ \boldsymbol d_{PN3,x},& \boldsymbol d_{PN3,y},& \boldsymbol d_{PN3,z}\\ \boldsymbol d_{PN4,x},& \boldsymbol d_{PN4,y},& \boldsymbol d_{PN4,z}\\ \boldsymbol d_{PN5,x},& \boldsymbol d_{PN5,y},& \boldsymbol d_{PN5,z}\\ \boldsymbol d_{PN6,x},& \boldsymbol d_{PN6,y},& \boldsymbol d_{PN6,z}\\ \end{matrix} \right ] \end{aligned} \left [ \begin{matrix} \frac{\partial T}{\partial x} \\ \frac{\partial T}{\partial y}\\ \frac{\partial T}{\partial z}\\ \end{matrix} \right ] = \begin{aligned} \left [ \begin{matrix} T_1-T_P\\ T_2-T_P\\ T_3-T_P \\ T_4-T_P\\ T_5-T_P\\ T_6-T_P\\ \end{matrix} \right ] \end{aligned}
⎣
⎡dPN1,x,dPN2,x,dPN3,x,dPN4,x,dPN5,x,dPN6,x,dPN1,y,dPN2,y,dPN3,y,dPN4,y,dPN5,y,dPN6,y,dPN1,zdPN2,zdPN3,zdPN4,zdPN5,zdPN6,z⎦
⎤⎣
⎡∂x∂T∂y∂T∂z∂T⎦
⎤=⎣
⎡T1−TPT2−TPT3−TPT4−TPT5−TPT6−TP⎦
⎤
[
d
P
N
]
[
(
∇
T
)
P
]
=
[
T
N
−
T
P
]
[\boldsymbol d_{PN}][(\nabla T)_P]=[T_N-T_P]
[dPN][(∇T)P]=[TN−TP]
A
X
=
B
\boldsymbol{AX=B}
AX=B
6
×
3
,
3
×
1
,
3
×
1
6\times3, 3\times1, 3\times1
6×3,3×1,3×1
N sided:
N
×
3
,
3
×
1
,
N
×
1
N\times3, 3\times1, N\times1
N×3,3×1,N×1
Least-Square Solution for ( ∇ T ) P (\nabla T)_P (∇T)P
[
d
P
N
]
[
(
∇
T
)
P
]
=
[
T
N
−
T
P
]
[\boldsymbol d_{PN}][(\nabla T)_P]=[T_N-T_P]
[dPN][(∇T)P]=[TN−TP]
d
P
N
d
P
N
T
(
∇
T
)
P
=
(
T
N
−
T
P
)
d
P
N
T
\boldsymbol d_{PN}\boldsymbol d_{PN}^T(\nabla T)_P=(T_N-T_P)\boldsymbol d_{PN}^T
dPNdPNT(∇T)P=(TN−TP)dPNT
( ∇ T ) P = ( d P N d P N T ) − 1 d P N T ( T N − T P ) (\nabla T)_P=(\boldsymbol d_{PN}\boldsymbol d_{PN}^T)^{-1}\boldsymbol d_{PN}^T(T_N-T_P) (∇T)P=(dPNdPNT)−1dPNT(TN−TP)
G = ( d P N d P N T ) G=(\boldsymbol d_{PN}\boldsymbol d_{PN}^T) G=(dPNdPNT)
( ∇ T ) P = G − 1 d P N T ( T N − T P ) (\nabla T)_P=G^{-1}\boldsymbol d_{PN}^T(T_N-T_P) (∇T)P=G−1dPNT(TN−TP)
example
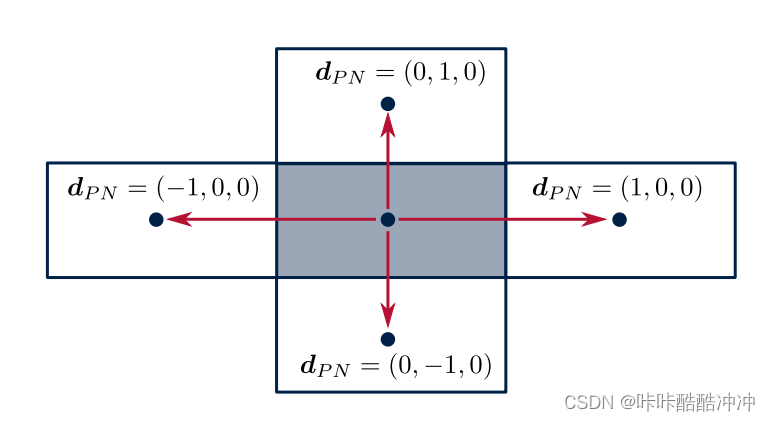
A
=
[
−
1
,
0
,
0
0
,
−
1
,
0
1
,
0
,
0
0
,
1
,
0
]
A
T
=
[
−
1
,
0
,
1
,
0
0
,
−
1
,
0
,
1
0
,
0
,
0
,
0
]
A= \begin{aligned} \left [ \begin{matrix} -1,&0,& 0\\ 0,&-1,& 0\\ 1,&0,& 0\\ 0,&1,& 0\\ \end{matrix} \right ] \end{aligned} A^T= \begin{aligned} \left [ \begin{matrix} -1,&0,&1,&0\\ 0,&-1,& 0,&1\\ 0,&0,& 0,&0\\ \end{matrix} \right ] \end{aligned}
A=⎣
⎡−1,0,1,0,0,−1,0,1,0000⎦
⎤AT=⎣
⎡−1,0,0,0,−1,0,1,0,0,010⎦
⎤
G
=
A
A
T
=
[
2
,
0
,
0
0
,
2
,
0
0
,
0
,
0
]
G
−
1
=
[
1
2
,
0
,
0
0
,
1
2
,
0
0
,
0
,
0
]
G=AA^T= \begin{aligned} \left [ \begin{matrix} 2,&0,&0\\ 0,&2,&0\\ 0,&0,& 0\\ \end{matrix} \right ] \end{aligned} G^{-1}= \begin{aligned} \left [ \begin{matrix} \frac{1}{2},&0,&0\\ 0,&\frac{1}{2},&0\\ 0,&0,& 0\\ \end{matrix} \right ] \end{aligned}
G=AAT=⎣
⎡2,0,0,0,2,0,000⎦
⎤G−1=⎣
⎡21,0,0,0,21,0,000⎦
⎤
逆矩阵求解方法可以参考:
- book- introduction to linear algebra (Gilbert Strang) C2.5 inverse matrices
- YouTube-3. Multiplication and Inverse Matrices
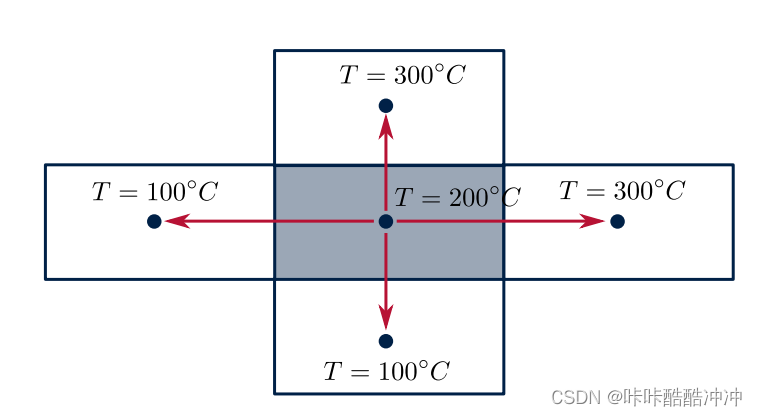
(
∇
T
)
P
=
G
−
1
d
P
N
T
(
T
N
−
T
P
)
(\nabla T)_P=G^{-1}\boldsymbol d_{PN}^T(T_N-T_P)
(∇T)P=G−1dPNT(TN−TP)
(
∇
T
)
P
=
[
1
2
,
0
,
0
0
,
1
2
,
0
0
,
0
,
0
]
[
−
1
,
0
,
1
,
0
0
,
−
1
,
0
,
1
0
,
0
,
0
,
0
]
[
100
−
200
100
−
200
300
−
200
300
−
200
]
=
[
∂
T
∂
x
∂
T
∂
y
∂
T
∂
z
]
=
[
100
100
0
]
(\nabla T)_P= \begin{aligned} \left [ \begin{matrix} \frac{1}{2},&0,&0\\ 0,&\frac{1}{2},&0\\ 0,&0,& 0\\ \end{matrix} \right ] \end{aligned} \left [ \begin{matrix} -1,&0,&1,&0\\ 0,&-1,& 0,&1\\ 0,&0,& 0,&0\\ \end{matrix} \right ] \begin{aligned} \left [ \begin{matrix} 100-200\\ 100-200\\ 300-200\\ 300-200\\ \end{matrix} \right ] \end{aligned}= \begin{aligned} \left [ \begin{matrix} \frac{\partial T}{\partial x} \\ \frac{\partial T}{\partial y}\\ \frac{\partial T}{\partial z}\\ \end{matrix} \right ] \end{aligned}= \begin{aligned} \left [ \begin{matrix} 100\\ 100\\ 0\\ \end{matrix} \right ] \end{aligned}
(∇T)P=⎣
⎡21,0,0,0,21,0,000⎦
⎤⎣
⎡−1,0,0,0,−1,0,1,0,0,010⎦
⎤⎣
⎡100−200100−200300−200300−200⎦
⎤=⎣
⎡∂x∂T∂y∂T∂z∂T⎦
⎤=⎣
⎡1001000⎦
⎤
方法2:
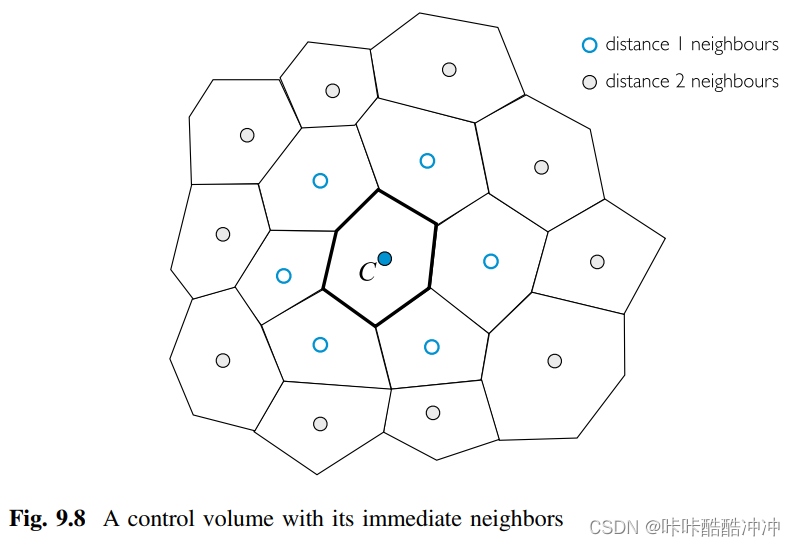
[
∑
k
=
1
N
B
(
C
)
w
k
Δ
x
k
Δ
x
k
,
∑
k
=
1
N
B
(
C
)
w
k
Δ
x
k
Δ
y
k
,
∑
k
=
1
N
B
(
C
)
w
k
Δ
x
k
Δ
z
k
∑
k
=
1
N
B
(
C
)
w
k
Δ
y
k
Δ
x
k
,
∑
k
=
1
N
B
(
C
)
w
k
Δ
y
k
Δ
y
k
,
∑
k
=
1
N
B
(
C
)
w
k
Δ
y
k
Δ
z
k
∑
k
=
1
N
B
(
C
)
w
k
Δ
z
k
Δ
x
k
,
∑
k
=
1
N
B
(
C
)
w
k
Δ
z
k
Δ
y
k
,
∑
k
=
1
N
B
(
C
)
w
k
Δ
z
k
Δ
z
k
]
[
(
∂
ϕ
∂
x
)
C
(
∂
ϕ
∂
y
)
C
(
∂
ϕ
∂
z
)
C
]
=
[
∑
k
=
1
N
B
(
C
)
w
k
Δ
x
k
Δ
ϕ
k
∑
k
=
1
N
B
(
C
)
w
k
Δ
y
k
Δ
ϕ
k
∑
k
=
1
N
B
(
C
)
w
k
Δ
z
k
Δ
ϕ
k
]
\begin{aligned} \left [ \begin{matrix} \sum^{NB(C)}_{k=1}w_k\Delta x_k\Delta x_k,& \sum^{NB(C)}_{k=1}w_k\Delta x_k\Delta y_k,& \sum^{NB(C)}_{k=1}w_k\Delta x_k\Delta z_k\\ \sum^{NB(C)}_{k=1}w_k\Delta y_k\Delta x_k,& \sum^{NB(C)}_{k=1}w_k\Delta y_k\Delta y_k,& \sum^{NB(C)}_{k=1}w_k\Delta y_k\Delta z_k\\ \sum^{NB(C)}_{k=1}w_k\Delta z_k\Delta x_k,& \sum^{NB(C)}_{k=1}w_k\Delta z_k\Delta y_k,& \sum^{NB(C)}_{k=1}w_k\Delta z_k\Delta z_k\\ \end{matrix} \right ] \end{aligned} \left [ \begin{matrix} (\frac{\partial \phi}{\partial x})_C \\ (\frac{\partial \phi}{\partial y})_C\\ (\frac{\partial \phi}{\partial z})_C\\ \end{matrix} \right ] = \begin{aligned} \left [ \begin{matrix} \sum^{NB(C)}_{k=1}w_k\Delta x_k\Delta \phi_k\\ \sum^{NB(C)}_{k=1}w_k\Delta y_k\Delta \phi_k\\ \sum^{NB(C)}_{k=1}w_k\Delta z_k\Delta \phi_k\\ \end{matrix} \right ] \end{aligned}
⎣
⎡∑k=1NB(C)wkΔxkΔxk,∑k=1NB(C)wkΔykΔxk,∑k=1NB(C)wkΔzkΔxk,∑k=1NB(C)wkΔxkΔyk,∑k=1NB(C)wkΔykΔyk,∑k=1NB(C)wkΔzkΔyk,∑k=1NB(C)wkΔxkΔzk∑k=1NB(C)wkΔykΔzk∑k=1NB(C)wkΔzkΔzk⎦
⎤⎣
⎡(∂x∂ϕ)C(∂y∂ϕ)C(∂z∂ϕ)C⎦
⎤=⎣
⎡∑k=1NB(C)wkΔxkΔϕk∑k=1NB(C)wkΔykΔϕk∑k=1NB(C)wkΔzkΔϕk⎦
⎤
w
k
=
1
∣
r
F
k
−
r
C
∣
=
1
Δ
x
F
k
2
+
Δ
y
F
k
2
+
Δ
y
F
k
2
w_k=\frac{1}{\left|\boldsymbol r_{Fk}-\boldsymbol r_C\right|}=\frac{1}{\sqrt{\Delta x^2_{F_k}+\Delta y^2_{F_k}+\Delta y^2_{F_k}}}
wk=∣rFk−rC∣1=ΔxFk2+ΔyFk2+ΔyFk21
[
x
E
−
x
W
,
0
,
0
0
,
y
N
−
y
S
,
0
0
,
0
,
z
T
−
z
B
]
[
(
∂
ϕ
∂
x
)
C
(
∂
ϕ
∂
y
)
C
(
∂
ϕ
∂
z
)
C
]
=
[
ϕ
E
−
ϕ
W
ϕ
N
−
ϕ
S
ϕ
T
−
ϕ
B
]
\begin{aligned} \left [ \begin{matrix} x_E-x_W,&0,& 0\\ 0,&y_N-y_S,& 0\\ 0,&0,& z_T-z_B\\ \end{matrix} \right ] \end{aligned} \left [ \begin{matrix} (\frac{\partial \phi}{\partial x})_C \\ (\frac{\partial \phi}{\partial y})_C\\ (\frac{\partial \phi}{\partial z})_C\\ \end{matrix} \right ] = \begin{aligned} \left [ \begin{matrix} \phi_E-\phi_W\\ \phi_N-\phi_S\\ \phi_T-\phi_B\\ \end{matrix} \right ] \end{aligned}
⎣
⎡xE−xW,0,0,0,yN−yS,0,00zT−zB⎦
⎤⎣
⎡(∂x∂ϕ)C(∂y∂ϕ)C(∂z∂ϕ)C⎦
⎤=⎣
⎡ϕE−ϕWϕN−ϕSϕT−ϕB⎦
⎤
(
r
−
r
C
)
⋅
(
∇
ϕ
)
C
+
O
(
r
2
)
=
ϕ
(
r
)
−
ϕ
(
r
C
)
(\boldsymbol r-\boldsymbol r_C)\cdot(\nabla \phi)_C+O(\boldsymbol r^2)=\phi(\boldsymbol r)-\phi(\boldsymbol r_C)
(r−rC)⋅(∇ϕ)C+O(r2)=ϕ(r)−ϕ(rC)






















 1270
1270











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








