一、提升算法概论
Boosting(提升)是一族可将弱学习器提升为强学习器的算法。提升算法基于这样一种思想:对于一个复杂的任务,将多个专家的判断总和得出的结果要比任何一个专家单独的判断好。这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器表现对训练样本分布进行调整,是的先前基学习器做错的样本在后续收到更多关注(赋予做错的样本更大的权值),然后基于调整后的样本分布来训练下一个基学习器,一直反复进行,直到达到指定值。对样本加权的过程如下:

上图中被放大的点是被加权的样本,样本加权后,在下一次的学习中就会收到更多的关注。
也就是说提升算法对分类错误的样本更为关注,通过改变错误样本所占的权值来改变分类边界,从而一步步提升算法的准确度。
二、AdaBoost算法
AdaBoost算法是提升算法中最具代表性的。正如上面所说的,在AdaBoost算法中会提高前一轮分类器分类错误的样本的权值,而降低那些被分类正确样本的权值。对于弱分类器的组合,AdaBoost算法采取加权多数表决的方法。具体的说就是加大分类误差率小的弱分类器的权值,使其在表决中起到较大的作用;减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。下面具体说一下AdaBoost算法的流程。



关于AdaBoost算法做如下说明:


以上关于AdaBoost算法流程来自《统计学习方法》,更多关于AdaBoost算法内容可以参见《统计学习方法》
三、Gradient boosting(GB) 梯度提升算法
梯度提升算法首先给定一个目标损失函数,它的定义域是所有可行的若函数集合(基函数);提升算法通过迭代的选择一个负梯度方向上的基函数来逐渐逼近局部最小值。
梯度提升算法过程如下:
1.初始化模型为常数

2.1.计算伪残差(也就是梯度方向)

2.2.基于数据 计算拟合残差的基函数
计算拟合残差的基函数 (基函数也就是基学习器,例如决策树等算法)
(基函数也就是基学习器,例如决策树等算法)
2.3.计算最优的步长gamma,L是损失函数,通过经验风险最小化来选取参数gamma:
2.4.更新模型
四、GBDT(Gradient Boosting Decision Tree) 梯度提升决策树算法
GB算法中最典型的基学习器是决策树,尤其是CART,正如名字的含义,GBDT是GB和DT的结合。要注意的是这里的决策树是回归树,GBDT中的决策树是个弱模型,深度较小一般不会超过5,叶子节点的数量也不会超过10,对于生成的每棵决策树乘上比较小的缩减系数(学习率<0.1),有些GBDT的实现加入了随机抽样(subsample 0.5<=f <=0.8)提高模型的泛化能力。通过交叉验证的方法选择最优的参数。因此GBDT实际的核心问题变成怎么基于 使用CART决策树树生成
使用CART决策树树生成 (下面用tm(x)表示)。
(下面用tm(x)表示)。
在梯度提升中是根据伪残差数据计算基学习器的。令树tm(x)的叶节点数目为J,也就是将输入划分为J个不相交的区域,并且决策树tm(x)可以在每个区域中给出某个类型的确定性预测。使用指示记号I(x),对于输入x,tm(x)为:
bjm是样本x在第j个区域的预测值。
在GB算法的更新和gamma的选择中,将上式带入到h(x)中、
即对于:
将
tm(x)带入到hm(x)中可得:
代入时,将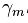
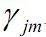
其余步骤和GB算法类似。
五、XGBoost算法
XGBoost是提升算法的高效实现,在各项机器学习、大数据比赛中的效果非常好。下面简要介绍一下其推导过程。
XGBoost与GBDT主要的不同在于其目标函数使用了正则项并且利用了二阶导数信息,如下式:
红色箭头指向的l即为损失函数;红色方框为正则项,包括L1、L2;红色圆圈为常数项。xgboost利用泰勒展开三项,做一个近似,我们可以很清晰地看到,最终的目标函数只依赖于每个数据点的在误差函数上的一阶导数和二阶导数。
对上式做进一步化简:

对于上式中的累加和,可以做以下变换:

最终公式可以化简为:

通过对 求导等于0,可以得到
求导等于0,可以得到

然后把 最优解代入得到:
最优解代入得到:

打分函数
Obj代表了当我们指定一个树的结构的时候,我们在目标上面最多减少多少。我们可以把它叫做结构分数(structure score)

参考文献:
周志华《机器学习》
李航《统计学习方法》
邹博 机器学习视频与pdf
http://blog.csdn.net/a819825294/article/details/51206410
http://blog.csdn.net/weiyongle1996/article/details/77483691
http://www.cnblogs.com/liuwu265/p/4694191.html








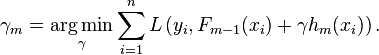
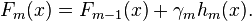
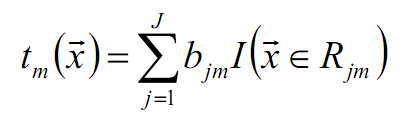

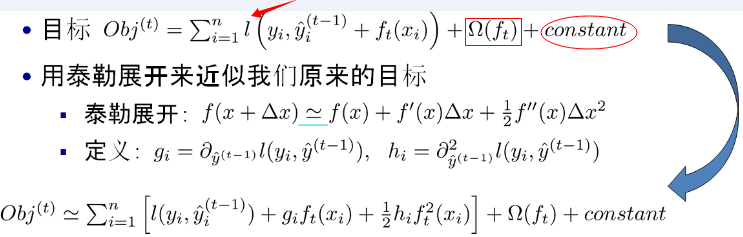














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








