差分约束<基础题练习><我是图论渣TAT>

今天有位神犇问我差分约束那道题怎么做QAQ
然而我这么弱怎么可能会那道题QAQ
所以先来介绍下什么是差分约束：

---

最短路：
dis[v] <= dis[x] + w(x,v);
那么我们考虑：
如果有一些约束，形如：
$b - a <= k_1$
$c - b <= k_2$
$c - a <= k_3$
求c - a的最大值.
那么怎么做呢？
考虑max{c - a}肯定恰好等于某一个约束。
证明：
若有m个约束，其中最大解maxn＜所有等式。
那么必然存在更大的解使得其解更优。
上面的都是我在胡言乱语
我们的max{c - a}肯定等于最小的那个约束没错吧。
如果我们考虑把上面的a,b,c分别建立点的话。
我们对a - > b连边，长度为$k_1$。这样$dis_b - dis_a <= k_1$
然后我们对其它点都进行连边，最后连成这个样子。

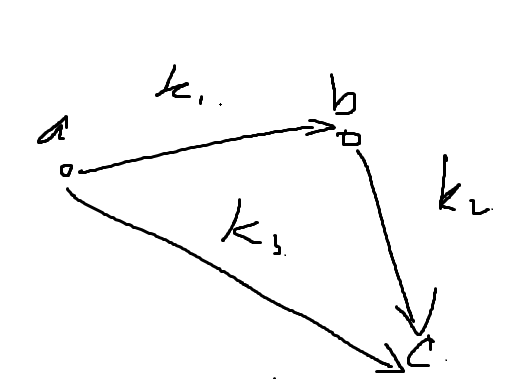
例子引自void - man的博客
那么我们求max{c - a}，也就是转化成了求a到c的最短路长度。
这样的话问题就解决了。

---

于是我打开了百度百科：
其实百度百科的例题还不错：
有n个盒子，每个盒子最多放一个球，现在m个区间[$a_i,b_i$]只能放$c_i$个球，求最多在这n个盒子里面放几个球。
对其求前缀和，则有：

$$S_i - S_{i - 1} <= 1$$
$$S_{b_i} - S_{a_i} <= c_i$$
这样我们对 $S_0...S_n$分别建出点来，跑一下SPFA，然后就能解决辣。
另外，建议一开始跑SPFA的时候增加附加源点，不然很容易挂。

---

以后应该去练习这些题了QAQ
感觉图论一点都不会……
其实fsf说得好像很有道理……
就是我根本不会图论数学和字符串。
QAQ