缘由
本来可以和上一篇博客写在一起的,但是今天整个下午我都被这个跳跃表纠缠了,缠的最后我还不能说自己完全全全的说得透,所以只好单开一篇博客了。所以我也只能说说对这个东西的感悟。我并不打算完整的叙述这个东西,这是因为
算法导论的公开课实在是讲的太透彻了,是否能够领悟看个人天资了。
参考来源
首先写这个是为了给看这篇博客的朋友有一个良好的引导:
先看看其空间复杂度:
- 空间复杂度: O(n) (期望)
- 跳跃表高度: O(logn)(期望)
相关操作的时间复杂度:
- 查找:O(logn)(期望)
- 插入: O(logn)(期望)
- 删除:O(logn)(期望)
上面5个都在
算法合集之《浅谈“跳跃表”的相关操作及其应用》有着让我似懂非懂的解释。有了上面的基础资料后,我打算讲讲我想说的话。
顶层链表元素的确定方式
底层链表就是最初的链表,包含所有元素。
- 在第20分钟,老师问:
we just like every node to be accessed sort of as quickly as possible, uniformly
我们只希望尽可能的访问每一个节点尽可能的快。那么什么样的元素应该添加进上层链表。 - 学生回到是:uniformly,我的理解就是均匀的让底层元素出现在上层链表中。
看下图,来自数据结构与算法分析—C语言描述 P300


在第一个上层链表中,其隔一个挑选了一个元素作为上层链表的元素。
在后来的视频中,老师用抛硬币的方式决定每一个节点是否应该出现在上层链表,那么每一个节点的概率都是1/2。如此来满足均匀的要求,进而满足了尽可能快的访问到每一个元素。
到底需要多少条额外的链表最合适?
就算到此之前的公开课的内容你都没听懂,那么在第三十分钟时,这位老师问:
- what's the biggest reasonable value of k that I could use?
- 译:k值到最大多少才合理?
- k就是额外的链表个数(额外这个词是我自己的理解)
然后老师解释说,由于访问速度是 k 乘以开k次方的n,所以为了 让这个数值最低,那么k取LogN最好,数学上的我不太擅长。
而这个logN很像二叉排序树的高度,那么大家都有感觉,就是这个跳跃链查找过程越来越像折半查找。所以这logN的取法,以这样的方式还是很容易让我明白的。
查找的过程和复杂度
由于我们已经确定了有多少个链表,所以来完整的走一遍查找某个元素的过程,那么就非常清楚其复杂度了。
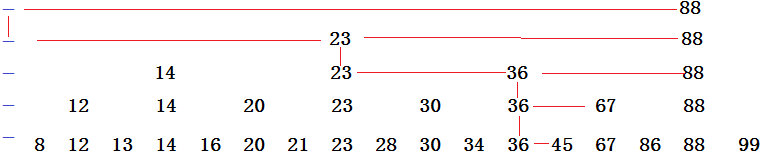
如下图所示:
- 最右边的蓝线代表负无穷
- 当然我们要查找45时,每一根红线代表我们查找的路径
- 横着代表比较了一下,竖着代表走向下层链表
- 我们可以认为刚开始有一个指针指着左上方的负无穷

- 从最上层的链表开始,第一个遇到的数是88,那么45在88之间,比较了一次,45小于88,所以走向下层链表。
- 45与23相比,大于23,那么再与88比较,发现小于88,所在在23处向下走
- 45与36相比,发现大于36,所以现在指针指36,再45与88比,又小了,所以在36处向下走
- 45与67比,发现小了,那么在36处向下走。
- 在底层链表与45比,发现一样,ok,找到了。
这就是查找过程,一共经历了移动了7次比较,挪动了4次指针。此时的需要的额外的链表为4个,加上底层链表一共是5个链表。
其中,注意比较次数,在每一条链表上我们可以发现最多比较两次,至少比较一次,所以比较次数不会超过 2LogN。
其中,注意比较次数,在每一条链表上我们可以发现最多比较两次,至少比较一次,所以比较次数不会超过 2LogN。
所以比较的时间复杂度是 O(logN)。
总结
我认为上面将最难得内容:查找 做了一个总结。公开课里也完整的、有趣的讲了插入和删除。当然还有更难的内容就是,在公开课的后半截,我基本上完全没听懂在在证明什么就放弃了。果然我还是做不了算法工程师,还是好好做的开发工程师吧。






















 1359
1359

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








