【Matlab】利用pdist和pdist2求各种距离

1.各种距离介绍

（1）.欧几里德距离Euclidean distance('euclidean')

        虽然很有用，但也有明显的缺点：
                a.它将样品的不同属性（即各指标或各变量）之间的差别等同看待，这一点有时不能满足实际要求；
                b.它没有考虑各变量的数量级(量纲)，容易犯大数吃小数的毛病。所以，可以先对原始数据进行规范化处理再进行距离计算。
（2）标准欧几里德距离Standardized Euclidean distance('seuclidean')

        相比单纯的欧氏距离，标准欧氏距离能够有效的解决上述缺点。注意，这里的V在许多Matlab函数中是可以自己设定的，不一定非得取标准差，可以依据各变量的重要程度设置不同的值，如knnsearch函数中的Scale属性。
（3）马哈拉诺比斯距离Mahalanobis distance('mahalanobis')

        马氏距离是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧式距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的(scale-invariant)，即独立于测量尺度。
        如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧式距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离.
马氏优缺点：

　　1）马氏距离的计算是建立在总体样本的基础上的，因为C是由总样本计算而来，所以马氏距离的计算是不稳定的；

　　2）在计算马氏距离过程中，要求总体样本数大于样本的维数。

　　3）协方差矩阵的逆矩阵可能不存在。  

（4）曼哈顿距离(城市区块距离)City block metric('cityblock')

（5）闵可夫斯基距离Minkowski metric('minkowski')

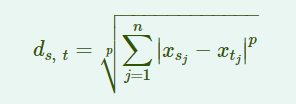
（6）切比雪夫距离Chebychev distance('chebychev')

（7）夹角余弦距离Cosine distance('cosine')

（8）相关距离Correlation distance('correlation')

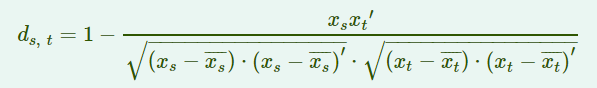
（9）汉明距离Hamming distance('hamming')

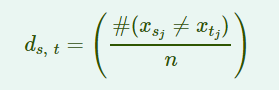
（10）杰卡德距离Jaccard distance('jaccard')

（11）Spearman distance('spearman') 

2.pdist

D = pidst(X)主要计算X的行的距离，例如输入X为m*n的矩阵，输出D为m*(m-1)/2的向量，计算方法如下例子：

X=[1,2;3,4;5,1] 3*2的矩阵;

pdist(X)计算结果为[2.8284,4.1231,3.6056];

3.pdist2

X为a*b矩阵，Y为c*b矩阵，矩阵的每一行代表一个元素，返回一个a*c矩阵，代表X，Y任意两个元素之间的距离。

 

参考自：

Matlab中 pdist 函数详解(各种距离的生成)

matlab中的pdist2函数